आर में शेफ़े परीक्षण कैसे करें

एक-तरफ़ा एनोवा का उपयोग यह निर्धारित करने के लिए किया जाता है कि तीन या अधिक स्वतंत्र समूहों के साधनों के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है या नहीं।

यदि एनोवा तालिका का समग्र पी-मूल्य एक निश्चित स्तर के महत्व से नीचे है, तो हमारे पास यह कहने के लिए पर्याप्त सबूत हैं कि समूह का कम से कम एक साधन दूसरों से अलग है।

हालाँकि, इससे हमें यह नहीं पता चलता कि कौन से समूह एक-दूसरे से भिन्न हैं। यह हमें बस इतना बताता है कि सभी समूहों का औसत समान नहीं है।

यह जानने के लिए कि कौन से समूह एक-दूसरे से भिन्न हैं, हमें एक पोस्ट-हॉक परीक्षण करने की आवश्यकता है जो प्रति परिवार त्रुटि दर को नियंत्रित कर सके।

सबसे अधिक उपयोग किए जाने वाले पोस्ट हॉक परीक्षणों में से एक शेफ़े परीक्षण है।

यह ट्यूटोरियल बताता है कि आर में शेफ़े परीक्षण कैसे करें।

उदाहरण: आर में शेफ़े परीक्षण

मान लीजिए कि एक शिक्षक जानना चाहता है कि क्या तीन अलग-अलग अध्ययन तकनीकों से छात्रों के बीच अलग-अलग परीक्षण स्कोर आते हैं या नहीं। इसका परीक्षण करने के लिए, वह यादृच्छिक रूप से 10 छात्रों को प्रत्येक अध्ययन तकनीक का उपयोग करने के लिए नियुक्त करती है और उनके परीक्षा परिणाम रिकॉर्ड करती है।

हम तीन समूहों के बीच औसत परीक्षा अंकों में अंतर का परीक्षण करने के लिए एक-तरफ़ा एनोवा को फिट करने के लिए आर में निम्नलिखित चरणों का उपयोग कर सकते हैं और यह निर्धारित करने के लिए कि कौन से समूह अलग हैं, शेफ़े परीक्षण का उपयोग कर सकते हैं।

चरण 1: डेटासेट बनाएं।

निम्नलिखित कोड दिखाता है कि सभी 30 छात्रों के परीक्षा परिणामों वाला डेटासेट कैसे बनाया जाए:

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

चरण 2: प्रत्येक समूह के लिए परीक्षा परिणाम देखें।

निम्नलिखित कोड दिखाता है कि प्रत्येक समूह के लिए परीक्षा परिणामों के वितरण की कल्पना करने के लिए बॉक्सप्लॉट कैसे तैयार करें:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

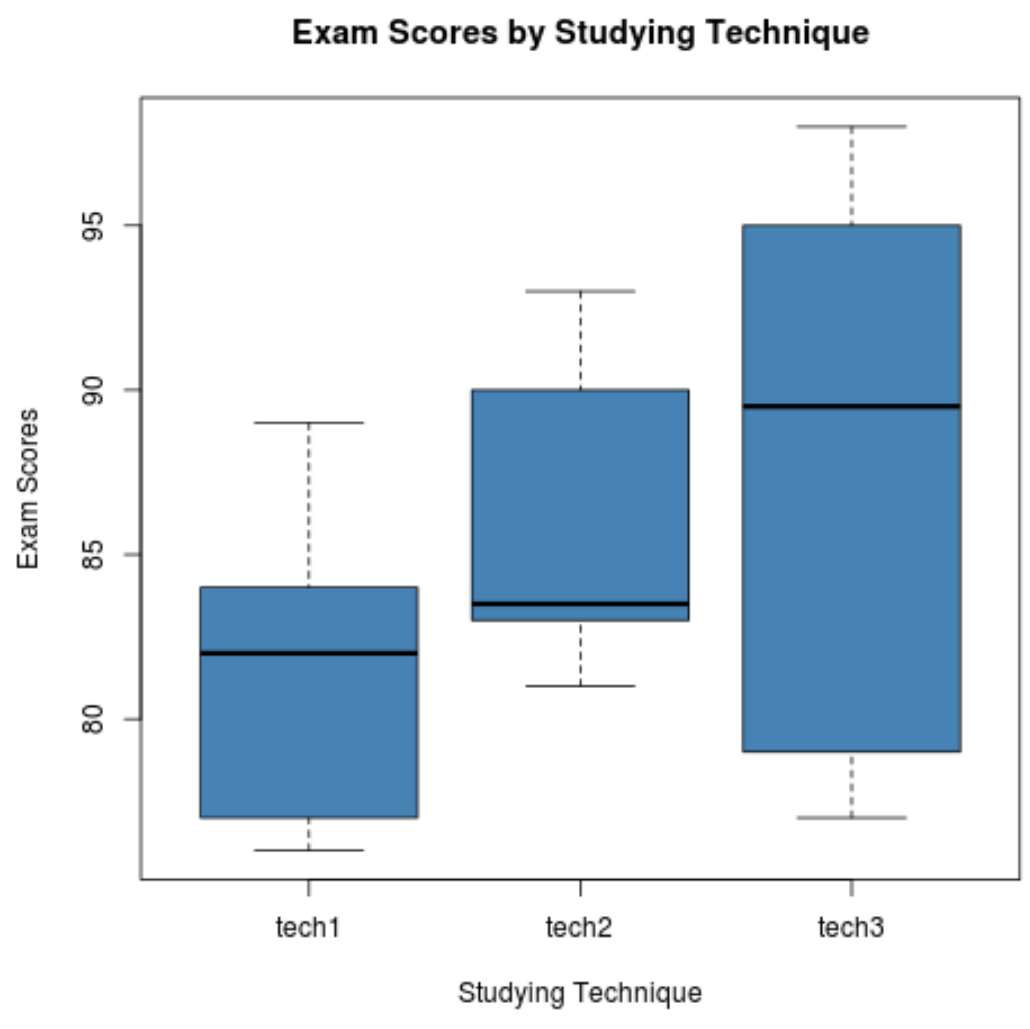
चरण 3: एक-तरफ़ा एनोवा निष्पादित करें।

निम्नलिखित कोड दिखाता है कि प्रत्येक समूह में औसत परीक्षा अंकों के बीच अंतर का परीक्षण करने के लिए एक-तरफ़ा एनोवा कैसे निष्पादित किया जाए:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

चूँकि समग्र पी-वैल्यू ( 0.0476 ) 0.05 से कम है, यह इंगित करता है कि प्रत्येक समूह का औसत परीक्षा स्कोर समान नहीं है।

इसके बाद, हम यह निर्धारित करने के लिए शेफ़े परीक्षण करेंगे कि कौन से समूह भिन्न हैं।

चरण 4: शेफ़ी परीक्षण करें।

शेफ़े परीक्षण करने के लिए, हम DescTools पैकेज से ScheffeTest() फ़ंक्शन का उपयोग करेंगे।

निम्नलिखित कोड दिखाता है कि हमारे उदाहरण के लिए इस फ़ंक्शन का उपयोग कैसे करें:

 #load DescTools package
library(DescTools)

#perform Scheffe's test
ScheffeTest(model)

  Posthoc multiple comparisons of means: Scheffe Test 
    95% family-wise confidence level

$technical
            diff lwr.ci upr.ci pval    
tech2-tech1 4.2 -2.24527202 10.645272 0.2582    
tech3-tech1 6.4 -0.04527202 12.845272 0.0519 .  
tech3-tech2 2.2 -4.24527202 8.645272 0.6803    

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

परिणाम की व्याख्या करने का तरीका इस प्रकार है:

• तकनीक 2 और तकनीक 1 के बीच परीक्षा परिणामों में औसत अंतर 4.2 है। माध्य अंतर के लिए संगत पी-मान 0.2582 है।
• तकनीक 3 और तकनीक 1 के बीच परीक्षा परिणामों में औसत अंतर 6.4 है। माध्य अंतर के लिए संगत पी-मान 0.0519 है।
• तकनीक 3 और तकनीक 2 के बीच परीक्षा परिणामों में औसत अंतर 2.2 है। माध्य अंतर के लिए संगत पी-मान 0.6803 है।

हम किस स्तर के महत्व का उपयोग करने का निर्णय लेते हैं, इसके आधार पर, केवल दो समूह जो सांख्यिकीय रूप से महत्वपूर्ण रूप से भिन्न दिखाई देते हैं, वे हैं तकनीक 3 और तकनीक 1।

अतिरिक्त संसाधन

आर में एकतरफ़ा एनोवा कैसे निष्पादित करें
आर में तुकी परीक्षण कैसे करें
आर में बोनफेरोनी सुधार कैसे करें