एकाधिक रैखिक प्रतिगमन की पाँच धारणाएँ

एकाधिक रेखीय प्रतिगमन एक सांख्यिकीय पद्धति है जिसका उपयोग हम एकाधिक भविष्यवक्ता चर और एक प्रतिक्रिया चर के बीच संबंध को समझने के लिए कर सकते हैं।

हालाँकि, एकाधिक रैखिक प्रतिगमन करने से पहले, हमें पहले यह सुनिश्चित करना होगा कि पाँच धारणाएँ पूरी हों:

1. रैखिक संबंध: प्रत्येक भविष्यवक्ता चर और प्रतिक्रिया चर के बीच एक रैखिक संबंध होता है।

2. कोई बहुसंरेखता नहीं: भविष्यवक्ता चर में से कोई भी एक दूसरे के साथ अत्यधिक सहसंबद्ध नहीं है।

3. स्वतंत्रता: अवलोकन स्वतंत्र हैं।

4. समरूपता: रैखिक मॉडल के प्रत्येक बिंदु पर अवशेषों में निरंतर भिन्नता होती है।

5. बहुभिन्नरूपी सामान्यता: मॉडल अवशेष सामान्य रूप से वितरित होते हैं।

यदि इनमें से एक या अधिक धारणाएं पूरी नहीं होती हैं, तो एकाधिक रैखिक प्रतिगमन के परिणाम विश्वसनीय नहीं हो सकते हैं।

इस लेख में, हम प्रत्येक धारणा के लिए एक स्पष्टीकरण प्रदान करते हैं, यह कैसे निर्धारित किया जाए कि धारणा पूरी हो गई है या नहीं, और यदि धारणा पूरी नहीं हुई है तो क्या करें।

परिकल्पना 1: रैखिक संबंध

एकाधिक रैखिक प्रतिगमन मानता है कि प्रत्येक भविष्यवक्ता चर और प्रतिक्रिया चर के बीच एक रैखिक संबंध है।

यह कैसे निर्धारित किया जाए कि यह धारणा पूरी हुई है या नहीं

यह निर्धारित करने का सबसे सरल तरीका है कि यह धारणा पूरी हुई है या नहीं, प्रत्येक भविष्यवक्ता चर और प्रतिक्रिया चर का एक स्कैटरप्लॉट बनाना है।

यह आपको स्पष्ट रूप से यह देखने की अनुमति देता है कि क्या दो चरों के बीच कोई रैखिक संबंध है।

यदि स्कैटरप्लॉट में बिंदु लगभग एक सीधी विकर्ण रेखा के साथ स्थित हैं, तो चर के बीच एक रैखिक संबंध होने की संभावना है।

उदाहरण के लिए, नीचे दिए गए ग्राफ़ में बिंदु एक सीधी रेखा पर आते प्रतीत होते हैं, जो दर्शाता है कि इस विशेष भविष्यवक्ता चर (x) और प्रतिक्रिया चर (y) के बीच एक रैखिक संबंध है:

यदि इस धारणा का सम्मान न किया जाए तो क्या करें?

यदि एक या अधिक भविष्यवक्ता चर और प्रतिक्रिया चर के बीच कोई रैखिक संबंध नहीं है, तो हमारे पास कई विकल्प हैं:

1. भविष्यवक्ता चर में एक गैर-रेखीय परिवर्तन लागू करें, उदाहरण के लिए लॉग या वर्गमूल लेना। यह अक्सर रिश्ते को अधिक रैखिक में बदल सकता है।

2. मॉडल में एक और भविष्यवक्ता चर जोड़ें। उदाहरण के लिए, यदि x बनाम y के प्लॉट में एक परवलयिक आकार है, तो मॉडल में एक अतिरिक्त भविष्यवक्ता चर के रूप में X ^{2 को} जोड़ने का अर्थ हो सकता है।

3. मॉडल से भविष्यवक्ता चर को हटा दें। सबसे चरम मामले में, यदि एक निश्चित भविष्यवक्ता चर और प्रतिक्रिया चर के बीच कोई रैखिक संबंध नहीं है, तो मॉडल में भविष्यवक्ता चर को शामिल करना उपयोगी नहीं हो सकता है।

परिकल्पना 2: कोई बहुसंरेखता नहीं

मल्टीपल लीनियर रिग्रेशन मानता है कि कोई भी भविष्यवक्ता चर एक-दूसरे के साथ अत्यधिक सहसंबद्ध नहीं है।

जब एक या अधिक भविष्यवक्ता चर अत्यधिक सहसंबद्ध होते हैं, तो प्रतिगमन मॉडल बहुसंरेखता से ग्रस्त हो जाता है, जिससे मॉडल का गुणांक अनुमान अविश्वसनीय हो जाता है।

यह कैसे निर्धारित किया जाए कि यह धारणा पूरी हुई है या नहीं

यह निर्धारित करने का सबसे सरल तरीका है कि यह धारणा पूरी हुई है या नहीं, प्रत्येक भविष्यवक्ता चर के लिए वीआईएफ मान की गणना करना है।

वीआईएफ मान 1 से शुरू होते हैं और इसकी कोई ऊपरी सीमा नहीं होती है। आम तौर पर, 5* से ऊपर वीआईएफ मान संभावित बहुसंरेखता का संकेत देते हैं।

निम्नलिखित ट्यूटोरियल दिखाते हैं कि विभिन्न सांख्यिकीय सॉफ़्टवेयर में वीआईएफ की गणना कैसे करें:

• आर में वीआईएफ की गणना कैसे करें
• पायथन में वीआईएफ की गणना कैसे करें
• एक्सेल में वीआईएफ की गणना कैसे करें

*कभी-कभी शोधकर्ता अध्ययन के क्षेत्र के आधार पर इसके बजाय 10 के वीआईएफ मान का उपयोग करते हैं।

यदि इस धारणा का सम्मान न किया जाए तो क्या करें?

यदि एक या अधिक भविष्यवक्ता चर का VIF मान 5 से अधिक है, तो इस समस्या को हल करने का सबसे आसान तरीका उच्च VIF मान वाले भविष्यवक्ता चर को हटाना है।

वैकल्पिक रूप से, यदि आप प्रत्येक भविष्यवक्ता चर को मॉडल में रखना चाहते हैं, तो आप एक अलग सांख्यिकीय पद्धति का उपयोग कर सकते हैं, जैसे कि रिज रिग्रेशन , लैस्सो रिग्रेशन , या आंशिक न्यूनतम वर्ग प्रतिगमन , जो अत्यधिक सहसंबद्ध भविष्यवक्ता चर को संभालने के लिए डिज़ाइन किया गया है।

परिकल्पना 3: स्वतंत्रता

एकाधिक रैखिक प्रतिगमन मानता है कि डेटा सेट में प्रत्येक अवलोकन स्वतंत्र है।

यह कैसे निर्धारित किया जाए कि यह धारणा पूरी हुई है या नहीं

यह निर्धारित करने का सबसे सरल तरीका है कि यह धारणा पूरी हुई है या नहीं, डर्बिन-वाटसन परीक्षण करना है, जो एक औपचारिक सांख्यिकीय परीक्षण है जो हमें बताता है कि अवशेष (और इसलिए अवलोकन) स्वत: सहसंबंध प्रदर्शित करते हैं या नहीं।

यदि इस धारणा का सम्मान न किया जाए तो क्या करें?

इस धारणा का उल्लंघन कैसे किया जाता है इसके आधार पर, आपके पास कई विकल्प हैं:

• सकारात्मक क्रमिक सहसंबंध के लिए, मॉडल में आश्रित और/या स्वतंत्र चर के अंतराल जोड़ने पर विचार करें।
• नकारात्मक क्रमिक सहसंबंध के लिए, सुनिश्चित करें कि आपका कोई भी चर अति-विलंबित नहीं है।
• मौसमी सहसंबंध के लिए, मॉडल में मौसमी डमी जोड़ने पर विचार करें।

परिकल्पना 4: समरूपता

एकाधिक रैखिक प्रतिगमन मानता है कि रैखिक मॉडल में प्रत्येक बिंदु पर अवशेषों में निरंतर भिन्नता होती है। जब ऐसा नहीं होता है, तो अवशेष विषमलैंगिकता से पीड़ित होते हैं।

जब प्रतिगमन विश्लेषण में विषमलैंगिकता मौजूद होती है, तो प्रतिगमन मॉडल के परिणाम अविश्वसनीय हो जाते हैं।

विशेष रूप से, विषमलैंगिकता प्रतिगमन गुणांक अनुमानों के विचरण को बढ़ाती है, लेकिन प्रतिगमन मॉडल इसका हिसाब नहीं देता है। इससे यह अधिक संभावना हो जाती है कि एक प्रतिगमन मॉडल यह दावा करेगा कि मॉडल में एक शब्द सांख्यिकीय रूप से महत्वपूर्ण है, जबकि वास्तव में ऐसा नहीं है।

यह कैसे निर्धारित किया जाए कि यह धारणा पूरी हुई है या नहीं

यह निर्धारित करने का सबसे आसान तरीका है कि यह धारणा पूरी हुई है या नहीं, पूर्वानुमानित मूल्यों के विरुद्ध मानकीकृत अवशेषों का एक प्लॉट बनाना है।

एक बार जब आप एक प्रतिगमन मॉडल को डेटा सेट में फिट कर लेते हैं, तो आप एक स्कैटरप्लॉट बना सकते हैं जो एक्स-अक्ष पर प्रतिक्रिया चर के अनुमानित मान और एक्स-अक्ष पर मॉडल के मानकीकृत अवशेषों को प्रदर्शित करता है। वाई

यदि स्कैटरप्लॉट में बिंदु एक प्रवृत्ति प्रदर्शित करते हैं, तो विषमलैंगिकता मौजूद है।

निम्नलिखित चार्ट एक प्रतिगमन मॉडल का एक उदाहरण दिखाता है जिसमें विषमलैंगिकता कोई समस्या नहीं है:

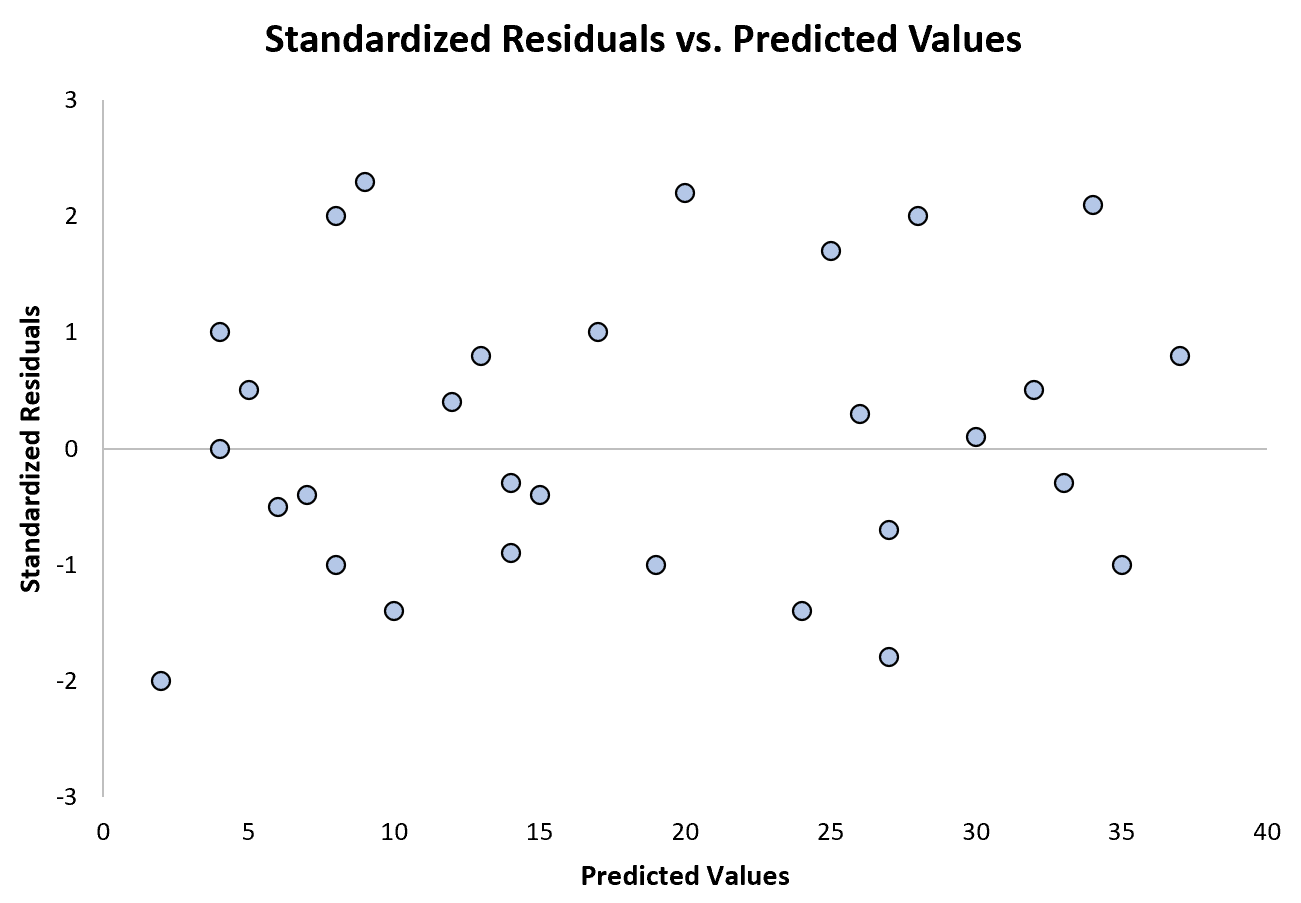
ध्यान दें कि मानकीकृत अवशेष बिना किसी स्पष्ट पैटर्न के शून्य के आसपास बिखरे हुए हैं।

निम्नलिखित चार्ट एक प्रतिगमन मॉडल का एक उदाहरण दिखाता है जहां विषमलैंगिकता एक समस्या है :

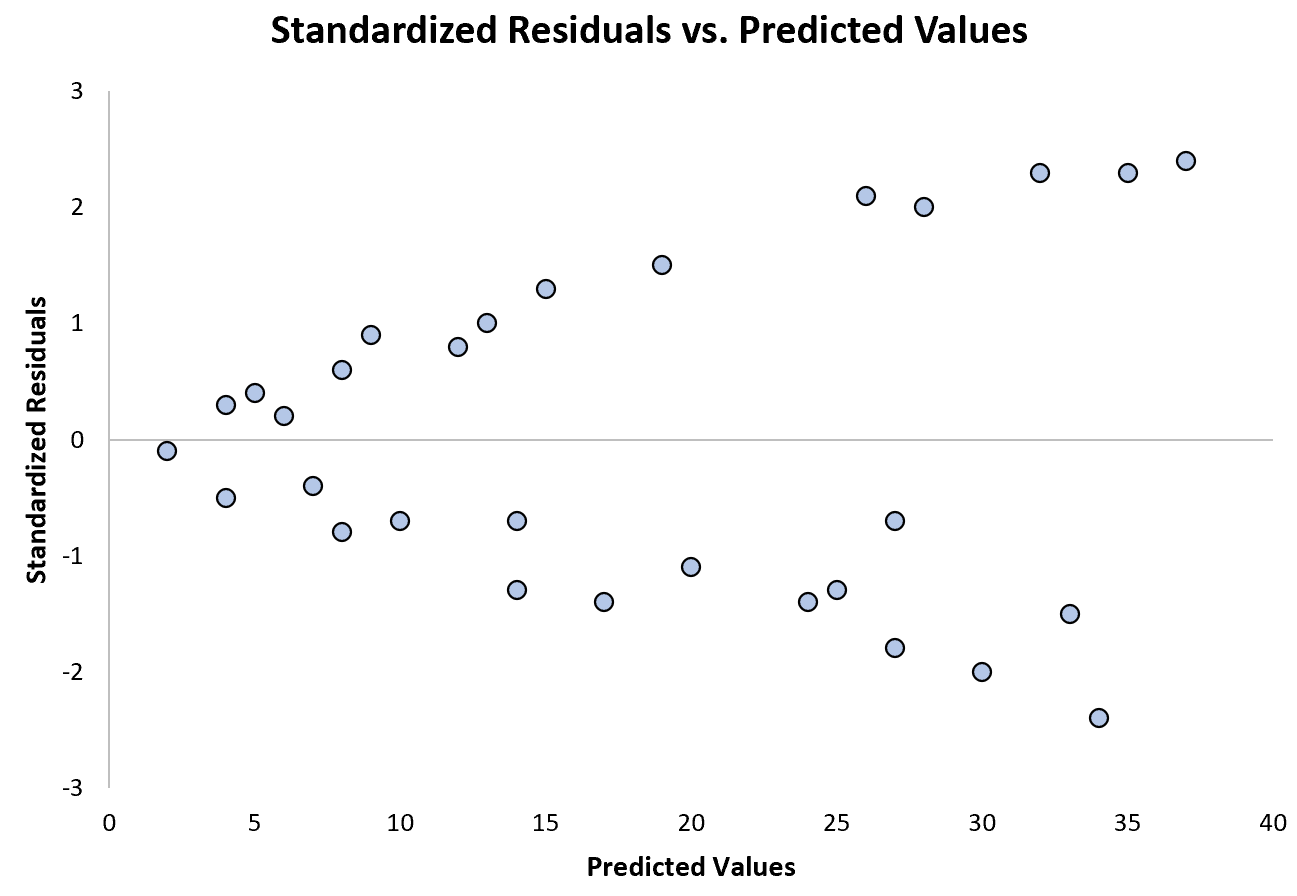
ध्यान दें कि पूर्वानुमानित मूल्यों में वृद्धि के साथ मानकीकृत अवशेष कैसे अधिक से अधिक फैलते हैं। यह “शंकु” आकार विषमलैंगिकता का एक उत्कृष्ट संकेत है:

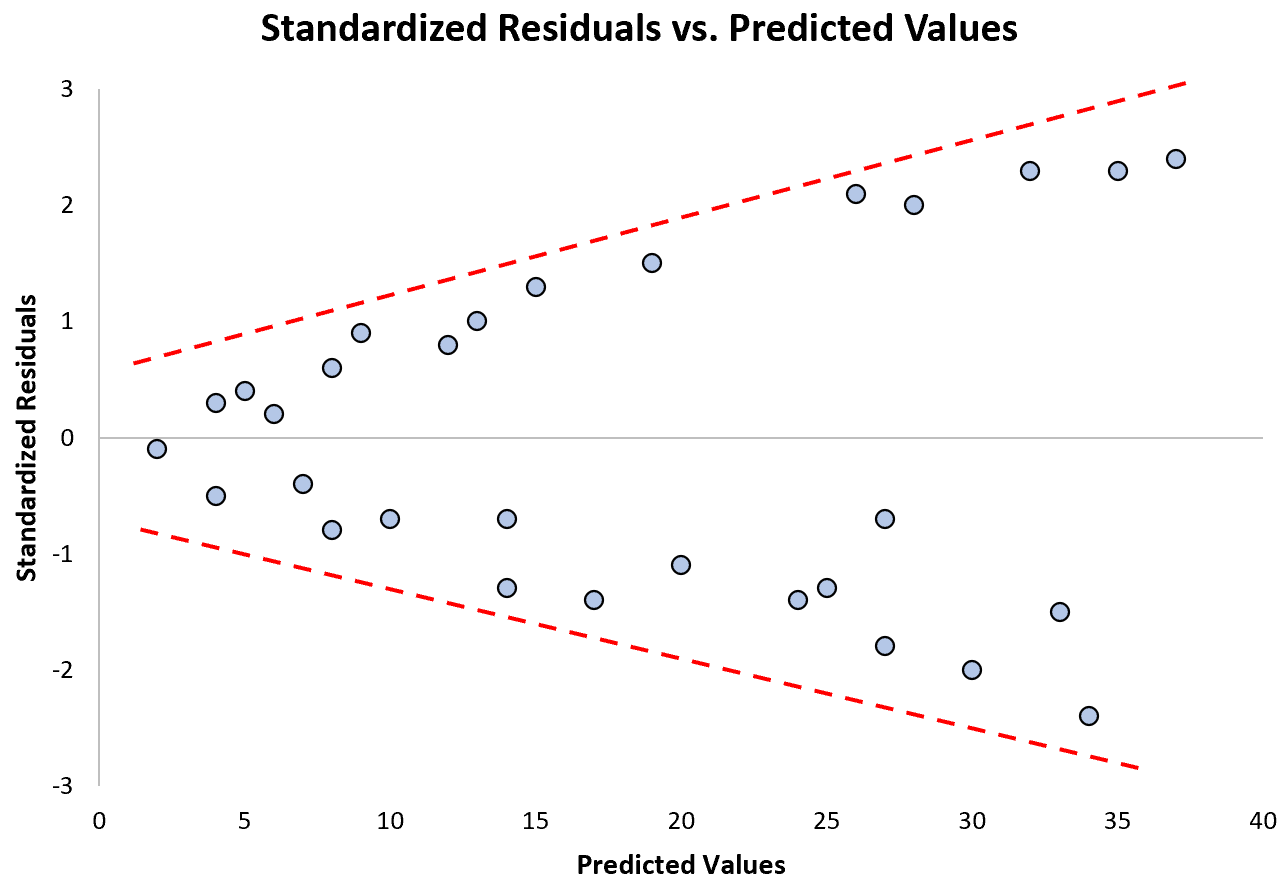
यदि इस धारणा का सम्मान न किया जाए तो क्या करें?

विषमलैंगिकता को ठीक करने के तीन सामान्य तरीके हैं:

1. प्रतिक्रिया चर को रूपांतरित करें। विषमलैंगिकता से निपटने का सबसे आम तरीका प्रतिक्रिया चर के सभी मानों का लॉग, वर्गमूल या घनमूल लेकर प्रतिक्रिया चर को बदलना है। इसके परिणामस्वरूप अक्सर विषमलैंगिकता का लोप हो जाता है।

2. प्रतिक्रिया चर को फिर से परिभाषित करें। प्रतिक्रिया चर को फिर से परिभाषित करने का एक तरीका कच्चे मूल्य के बजाय दर का उपयोग करना है। उदाहरण के लिए, किसी शहर में फूल विक्रेताओं की संख्या का अनुमान लगाने के लिए जनसंख्या आकार का उपयोग करने के बजाय, हम प्रति व्यक्ति फूल विक्रेताओं की संख्या का अनुमान लगाने के लिए जनसंख्या आकार का उपयोग कर सकते हैं।

ज्यादातर मामलों में, यह बड़ी आबादी के भीतर स्वाभाविक रूप से होने वाली परिवर्तनशीलता को कम कर देता है क्योंकि हम फूल विक्रेताओं की संख्या के बजाय प्रति व्यक्ति फूल विक्रेताओं की संख्या को माप रहे हैं।

3. भारित प्रतिगमन का प्रयोग करें. विषमलैंगिकता को ठीक करने का दूसरा तरीका भारित प्रतिगमन का उपयोग करना है, जो प्रत्येक डेटा बिंदु को उसके फिट मूल्य के भिन्नता के आधार पर एक भार प्रदान करता है।

अनिवार्य रूप से, यह उन डेटा बिंदुओं को कम महत्व देता है जिनमें अधिक भिन्नताएं होती हैं, जिससे उनके अवशिष्ट वर्ग कम हो जाते हैं। जब उचित वजन का उपयोग किया जाता है, तो यह विषमलैंगिकता की समस्या को समाप्त कर सकता है।

संबंधित : आर में भारित प्रतिगमन कैसे करें

धारणा 4: बहुभिन्नरूपी सामान्यता

एकाधिक रैखिक प्रतिगमन मानता है कि मॉडल अवशेष सामान्य रूप से वितरित किए जाते हैं।

यह कैसे निर्धारित किया जाए कि यह धारणा पूरी हुई है या नहीं

यह जांचने के दो सामान्य तरीके हैं कि यह धारणा संतुष्ट है या नहीं:

1. QQ प्लॉट का उपयोग करके परिकल्पना को दृश्य रूप से सत्यापित करें ।

QQ प्लॉट, क्वांटाइल-क्वांटाइल प्लॉट के लिए संक्षिप्त, एक प्रकार का प्लॉट है जिसका उपयोग हम यह निर्धारित करने के लिए कर सकते हैं कि किसी मॉडल के अवशेष सामान्य वितरण का पालन करते हैं या नहीं। यदि प्लॉट पर बिंदु मोटे तौर पर एक सीधी विकर्ण रेखा बनाते हैं, तो सामान्यता की धारणा पूरी होती है।

निम्नलिखित QQ प्लॉट अवशेषों का एक उदाहरण दिखाता है जो मोटे तौर पर सामान्य वितरण का अनुसरण करता है:

हालाँकि, नीचे दिया गया QQ प्लॉट एक ऐसे मामले का उदाहरण दिखाता है जहां अवशेष स्पष्ट रूप से एक सीधी विकर्ण रेखा से विचलित होते हैं, जो दर्शाता है कि वे सामान्य वितरण का पालन नहीं करते हैं:

2. शापिरो-विल्क, कोलमोगोरोव-स्मिरोनोव, जार्के-बैरे, या डी’ऑगोस्टिनो-पियर्सन जैसे औपचारिक सांख्यिकीय परीक्षण का उपयोग करके परिकल्पना को सत्यापित करें।

ध्यान रखें कि ये परीक्षण बड़े नमूना आकारों के प्रति संवेदनशील होते हैं – यानी, वे अक्सर यह निष्कर्ष निकालते हैं कि जब आपका नमूना आकार बहुत बड़ा होता है तो अवशेष सामान्य नहीं होते हैं। यही कारण है कि इस परिकल्पना को सत्यापित करने के लिए QQ प्लॉट जैसी ग्राफिकल विधियों का उपयोग करना अक्सर आसान होता है।

यदि इस धारणा का सम्मान न किया जाए तो क्या करें?

यदि सामान्यता की धारणा पूरी नहीं होती है, तो आपके पास कई विकल्प हैं:

1. सबसे पहले, जांचें कि डेटा में कोई चरम आउटलेर मौजूद नहीं है जिसके परिणामस्वरूप सामान्यता धारणा का उल्लंघन होता है।

2. फिर आप प्रतिक्रिया चर में एक अरेखीय परिवर्तन लागू कर सकते हैं, उदाहरण के लिए प्रतिक्रिया चर के सभी मानों का वर्गमूल, लॉग या घनमूल लेकर। इसके परिणामस्वरूप अक्सर मॉडल अवशेषों का अधिक सामान्य वितरण होता है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल एकाधिक रैखिक प्रतिगमन और इसकी मान्यताओं के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

एकाधिक रेखीय प्रतिगमन का परिचय
प्रतिगमन विश्लेषण में विषमलैंगिकता के लिए एक गाइड
प्रतिगमन में बहुसंरेखता और वीआईएफ के लिए एक गाइड

निम्नलिखित ट्यूटोरियल विभिन्न सांख्यिकीय सॉफ़्टवेयर का उपयोग करके एकाधिक रैखिक प्रतिगमन कैसे करें, इस पर चरण-दर-चरण उदाहरण प्रदान करते हैं:

एक्सेल में मल्टीपल लीनियर रिग्रेशन कैसे करें
आर में मल्टीपल लीनियर रिग्रेशन कैसे करें
एसपीएसएस में मल्टीपल लीनियर रिग्रेशन कैसे करें
स्टाटा में मल्टीपल लीनियर रिग्रेशन कैसे करें