एक्सेल में नमूना वितरण की गणना कैसे करें

एक नमूना वितरण एक एकल आबादी से कई यादृच्छिक नमूनों के आधार पर एक निश्चित आंकड़े का संभाव्यता वितरण है।

यह ट्यूटोरियल बताता है कि एक्सेल में नमूना वितरण के साथ निम्नलिखित कैसे करें:

• एक नमूना वितरण उत्पन्न करें.
• नमूना वितरण की कल्पना करें.
• नमूना वितरण के माध्य और मानक विचलन की गणना करें।
• नमूना वितरण के संबंध में संभावनाओं की गणना करें।

एक्सेल में एक नमूना वितरण उत्पन्न करें

मान लीजिए कि हम 1,000 नमूनों से युक्त एक नमूना वितरण उत्पन्न करना चाहते हैं जिसमें प्रत्येक नमूना आकार 20 है और 5.3 के माध्य और 9 के मानक विचलन के साथ सामान्य वितरण से आता है।

हम अपनी स्प्रैडशीट के सेल A2 में निम्नलिखित सूत्र टाइप करके आसानी से ऐसा कर सकते हैं:

 = NORM . INV ( RAND (), 5.3, 9)

हम तब तक सेल के निचले दाएं कोने पर होवर कर सकते हैं जब तक कि एक छोटा + दिखाई न दे और सूत्र को दाईं ओर 20 सेल और नीचे 1000 सेल तक खींचें:

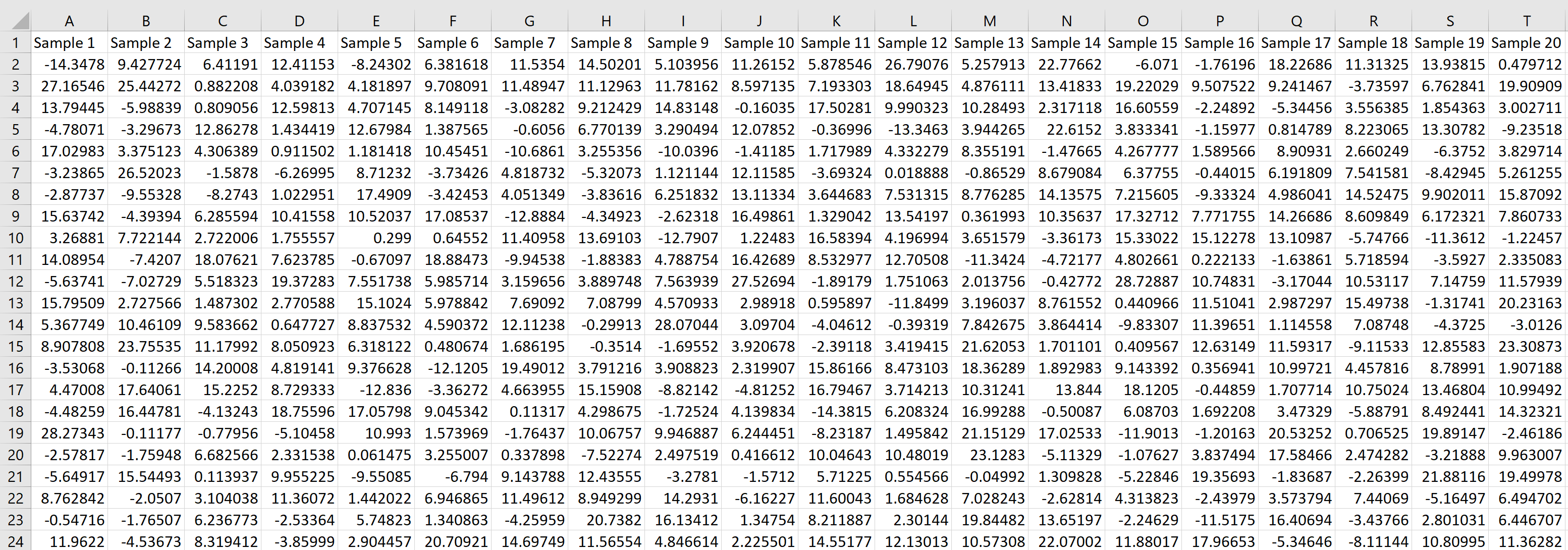
प्रत्येक पंक्ति आकार 20 के नमूने का प्रतिनिधित्व करती है जिसमें प्रत्येक मान 5.3 के माध्य और 9 के मानक विचलन के साथ सामान्य वितरण से आता है।

माध्य और मानक विचलन ज्ञात कीजिए

नमूना साधनों के इस नमूना वितरण का माध्य और मानक विचलन ज्ञात करने के लिए, हम पहले अपनी वर्कशीट के सेल U2 में निम्नलिखित सूत्र टाइप करके प्रत्येक नमूने का माध्य पा सकते हैं:

 = AVERAGE (A2:T2)

हम तब तक सेल के निचले दाएं कोने पर होवर कर सकते हैं जब तक कि एक छोटा + दिखाई न दे और इस फॉर्मूले को कॉलम U में अन्य सभी सेल में कॉपी करने के लिए डबल-क्लिक करें:

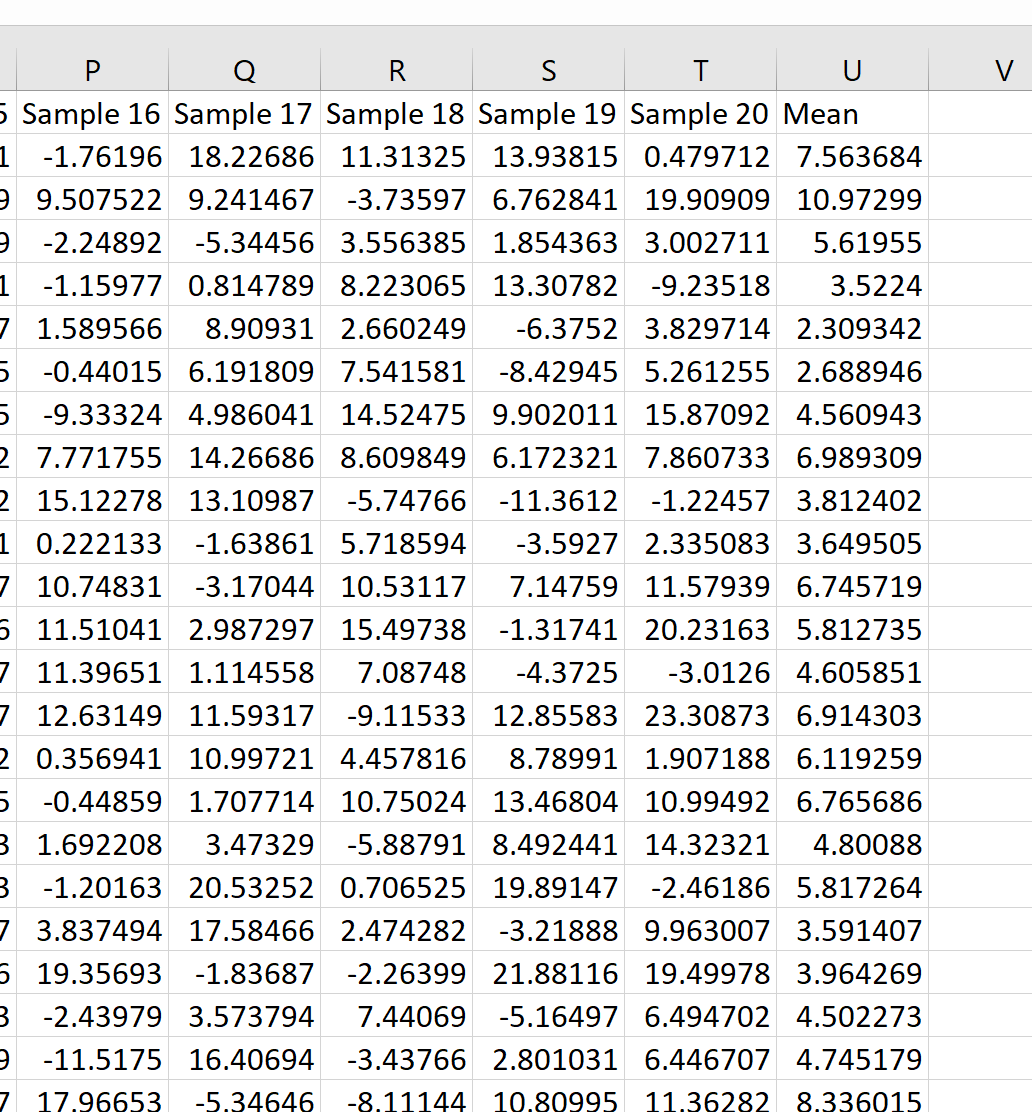
हम देख सकते हैं कि पहले नमूने का माध्य 7.563684 था, दूसरे नमूने का माध्य 10.97299 था, इत्यादि।

फिर हम नमूना माध्य के माध्य और मानक विचलन की गणना करने के लिए निम्नलिखित सूत्रों का उपयोग कर सकते हैं:

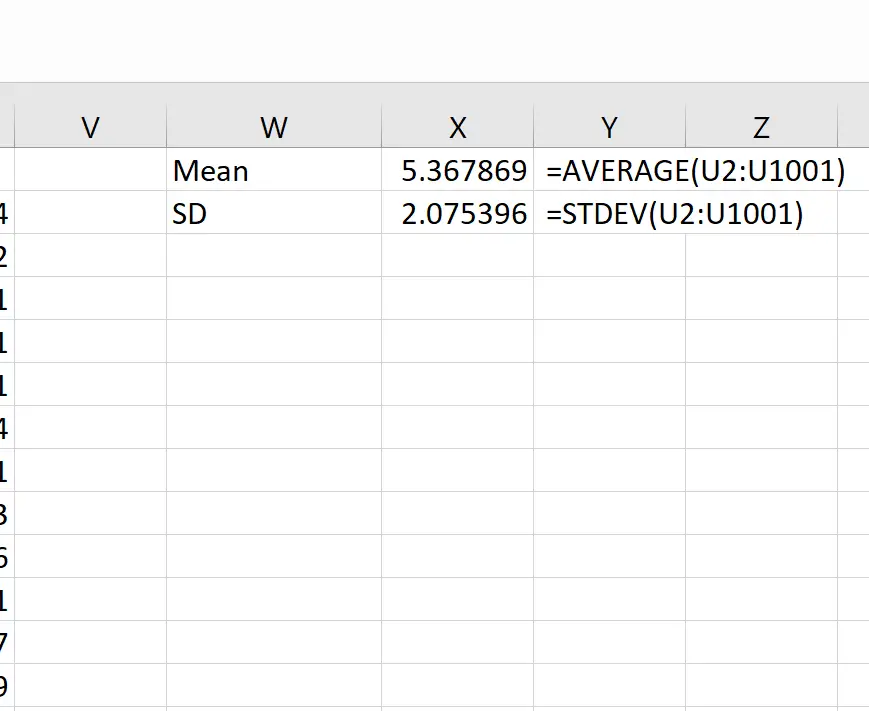
सैद्धांतिक रूप से, नमूना वितरण का माध्य 5.3 होना चाहिए। हम देख सकते हैं कि इस उदाहरण में वास्तविक नमूना माध्य 5.367869 है, जो 5.3 के करीब है।

और सैद्धांतिक रूप से, नमूना वितरण का मानक विचलन s/√n के बराबर होना चाहिए, जो 9 / √20 = 2.012 होगा। हम देख सकते हैं कि नमूना वितरण का वास्तविक मानक विचलन 2.075396 है, जो 2.012 के करीब है।

नमूना वितरण की कल्पना करें

हम नमूना साधनों के नमूना वितरण की कल्पना करने के लिए एक सरल हिस्टोग्राम भी बना सकते हैं।

ऐसा करने के लिए, बस कॉलम यू में सभी नमूना साधनों को हाइलाइट करें, सम्मिलित करें टैब पर क्लिक करें और फिर चार्ट अनुभाग के तहत हिस्टोग्राम विकल्प पर क्लिक करें।

यह निम्नलिखित हिस्टोग्राम देता है:

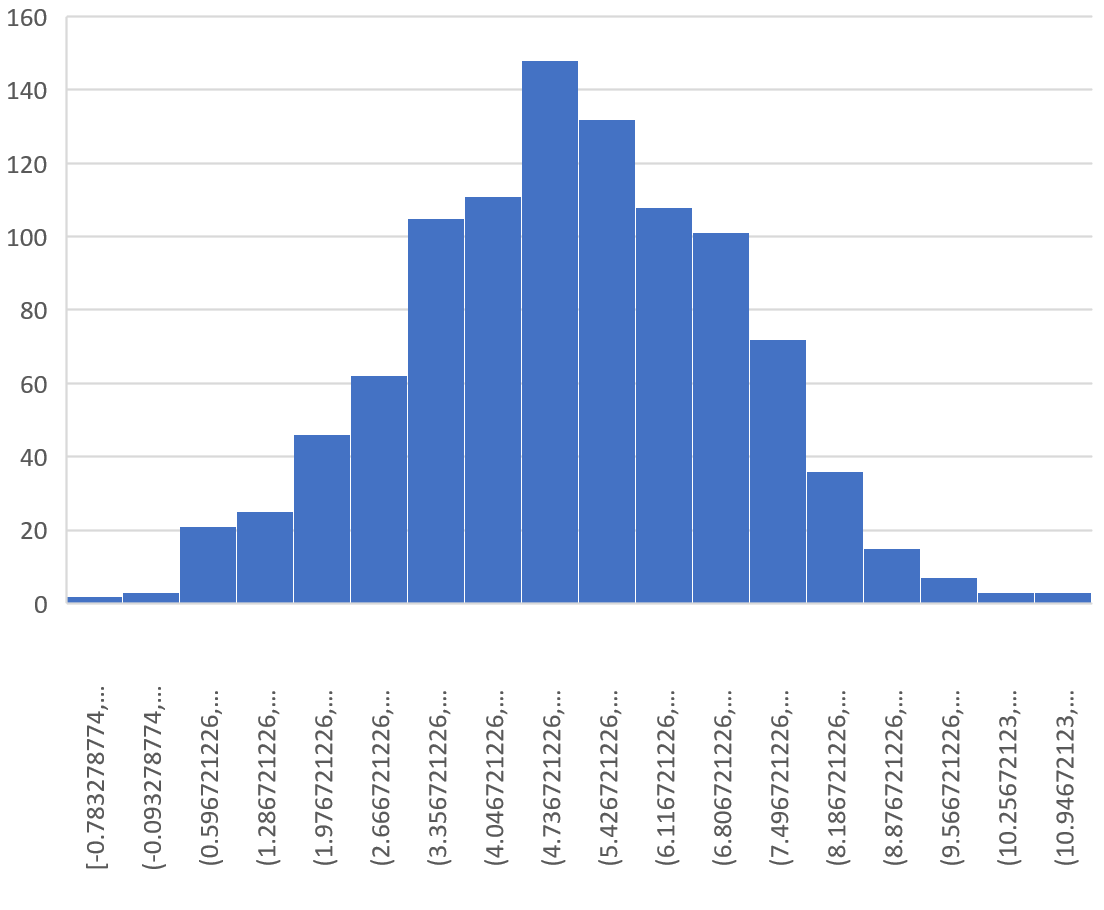
यह देखा जा सकता है कि नमूना वितरण घंटी के आकार का है जिसका शिखर मान 5 के करीब है।

हालाँकि, वितरण के विवरण से हम देख सकते हैं कि कुछ नमूनों का मतलब 10 से अधिक था और अन्य का मतलब 0 से कम था।

संभावनाओं की गणना करें

हम जनसंख्या माध्य, जनसंख्या मानक विचलन और नमूना आकार के आधार पर नमूना माध्य के लिए एक निश्चित मूल्य प्राप्त करने की संभावना की गणना भी कर सकते हैं।

उदाहरण के लिए, हम इस संभावना को खोजने के लिए निम्नलिखित सूत्र का उपयोग कर सकते हैं कि नमूना माध्य 6 से कम या उसके बराबर है, यह देखते हुए कि जनसंख्या माध्य 5.3 है, जनसंख्या मानक विचलन 9 है और नमूना आकार है:

 = COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)

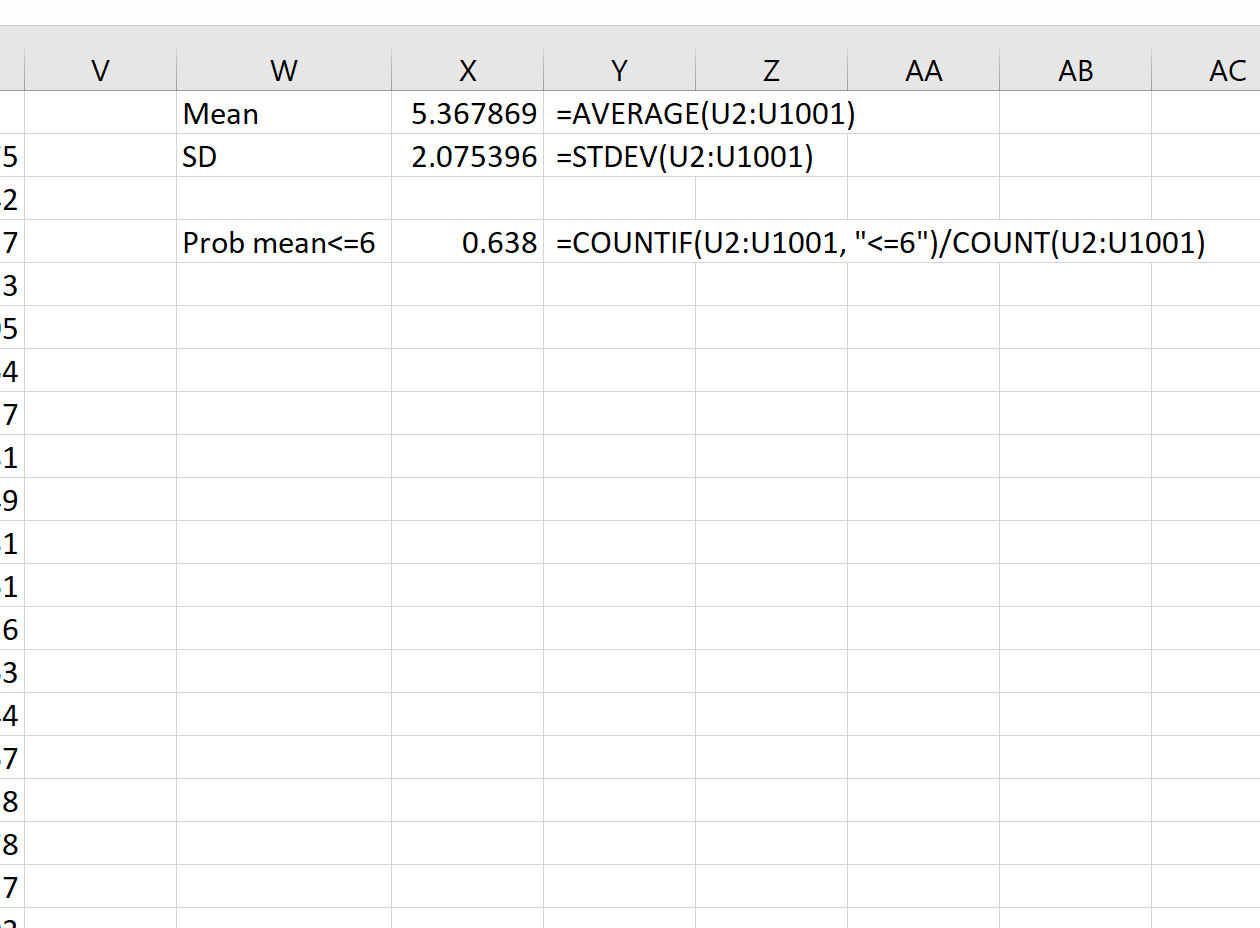
हम देखते हैं कि नमूना माध्य 6 से कम या उसके बराबर होने की प्रायिकता 0.638 है।

यह नमूनाकरण वितरण कैलकुलेटर द्वारा गणना की गई संभावना के बहुत करीब है:

अतिरिक्त संसाधन

नमूना वितरण का एक परिचय
नमूना वितरण कैलकुलेटर
केंद्रीय सीमा प्रमेय का एक परिचय