आर में क्रैमर-वॉन मिज़ टेस्ट कैसे करें (उदाहरण के साथ)

क्रैमर-वॉन मिज़ परीक्षण का उपयोग यह निर्धारित करने के लिए किया जाता है कि कोई नमूना सामान्य वितरण से आता है या नहीं।

इस प्रकार का परीक्षण यह निर्धारित करने के लिए उपयोगी है कि दिया गया डेटा सेट सामान्य वितरण से आता है या नहीं, जो कि प्रतिगमन , एनोवा , टी-परीक्षण और कई अन्य सहित कई सांख्यिकीय परीक्षणों में आमतौर पर इस्तेमाल की जाने वाली धारणा है। ‘अन्य।

हम R में goftest पैकेज से cvm.test() फ़ंक्शन का उपयोग करके आसानी से Cramer-Von Mises परीक्षण कर सकते हैं।

निम्नलिखित उदाहरण दिखाता है कि व्यवहार में इस फ़ंक्शन का उपयोग कैसे करें।

उदाहरण 1: सामान्य डेटा पर क्रैमर-वॉन मिज़ परीक्षण

निम्नलिखित कोड दिखाता है कि नमूना आकार n=100 वाले डेटासेट पर क्रैमर-वॉन मिज़ परीक्षण कैसे करें:

 library (goftest)

#make this example reproducible
set. seeds (0)

#create dataset of 100 random values generated from a normal distribution
data <- rnorm(100)

#perform Cramer-Von Mises test for normality
cvm. test (data, ' pnorm ')

	Cramer-von Mises test of goodness-of-fit
	Null hypothesis: Normal distribution
	Parameters assumed to be fixed

data:data
omega2 = 0.078666, p-value = 0.7007

परीक्षण का पी-मान 0.7007 निकला।

चूँकि यह मान 0.05 से कम नहीं है, हम मान सकते हैं कि नमूना डेटा सामान्य रूप से वितरित आबादी से आता है।

यह परिणाम आश्चर्यजनक नहीं होना चाहिए क्योंकि हमने rnorm() फ़ंक्शन का उपयोग करके नमूना डेटा तैयार किया है, जो मानक सामान्य वितरण से यादृच्छिक मान उत्पन्न करता है।

संबंधित: R में dnorm, pnorm, qnorm और rnorm के लिए एक गाइड

हम यह सत्यापित करने के लिए एक हिस्टोग्राम भी बना सकते हैं कि नमूना डेटा सामान्य रूप से वितरित किया गया है:

 hist(data, col=' steelblue ') 

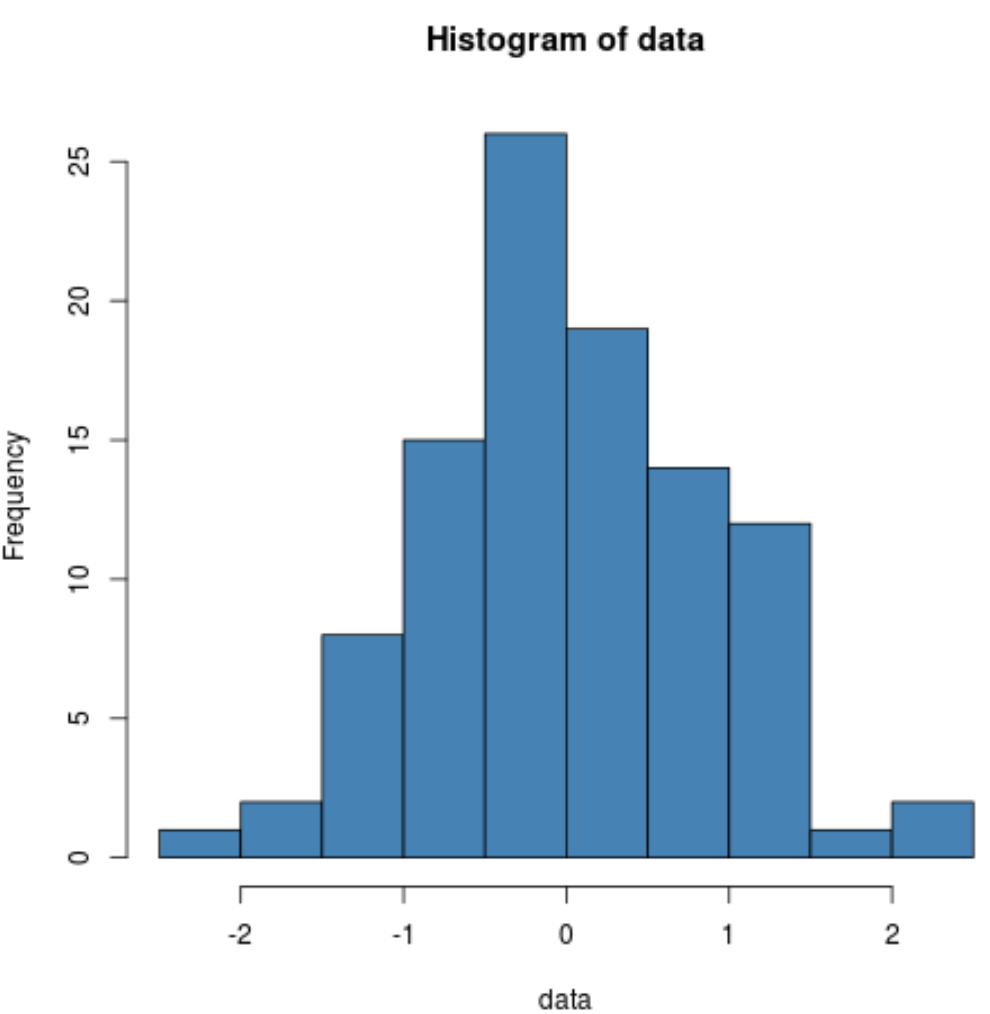
हम देख सकते हैं कि वितरण काफी घंटी के आकार का है और वितरण के केंद्र में एक शिखर है, जो सामान्य रूप से वितरित डेटा का विशिष्ट है।

उदाहरण 2: गैर-सामान्य डेटा पर क्रैमर-वॉन मिज़ परीक्षण

निम्नलिखित कोड दिखाता है कि 100 के नमूना आकार वाले डेटासेट पर क्रैमर-वॉन मिज़ परीक्षण कैसे करें जिसमें मान पॉइसन वितरण से यादृच्छिक रूप से उत्पन्न होते हैं:

 library (goftest)

#make this example reproducible
set. seeds (0)

#create dataset of 100 random values generated from a Poisson distribution
data <- rpois(n=100, lambda=3)

#perform Cramer-Von Mises test for normality
cvm. test (data, ' pnorm ')

	Cramer-von Mises test of goodness-of-fit
	Null hypothesis: Normal distribution
	Parameters assumed to be fixed

data:data
omega2 = 27.96, p-value < 2.2e-16

परीक्षण का पी-वैल्यू बेहद कम निकला।

चूँकि यह मान 0.05 से कम है, हमारे पास यह कहने के लिए पर्याप्त सबूत हैं कि नमूना डेटा सामान्य रूप से वितरित आबादी से नहीं आता है।

यह परिणाम आश्चर्यजनक नहीं होना चाहिए क्योंकि हमने rpois() फ़ंक्शन का उपयोग करके नमूना डेटा तैयार किया है, जो पॉइसन वितरण से यादृच्छिक मान उत्पन्न करता है।

संबंधित: R में dpois, ppois, qpois और rpois के लिए एक मार्गदर्शिका

हम यह देखने के लिए एक हिस्टोग्राम भी तैयार कर सकते हैं कि नमूना डेटा सामान्य रूप से वितरित नहीं है:

 hist(data, col=' coral2 ') 

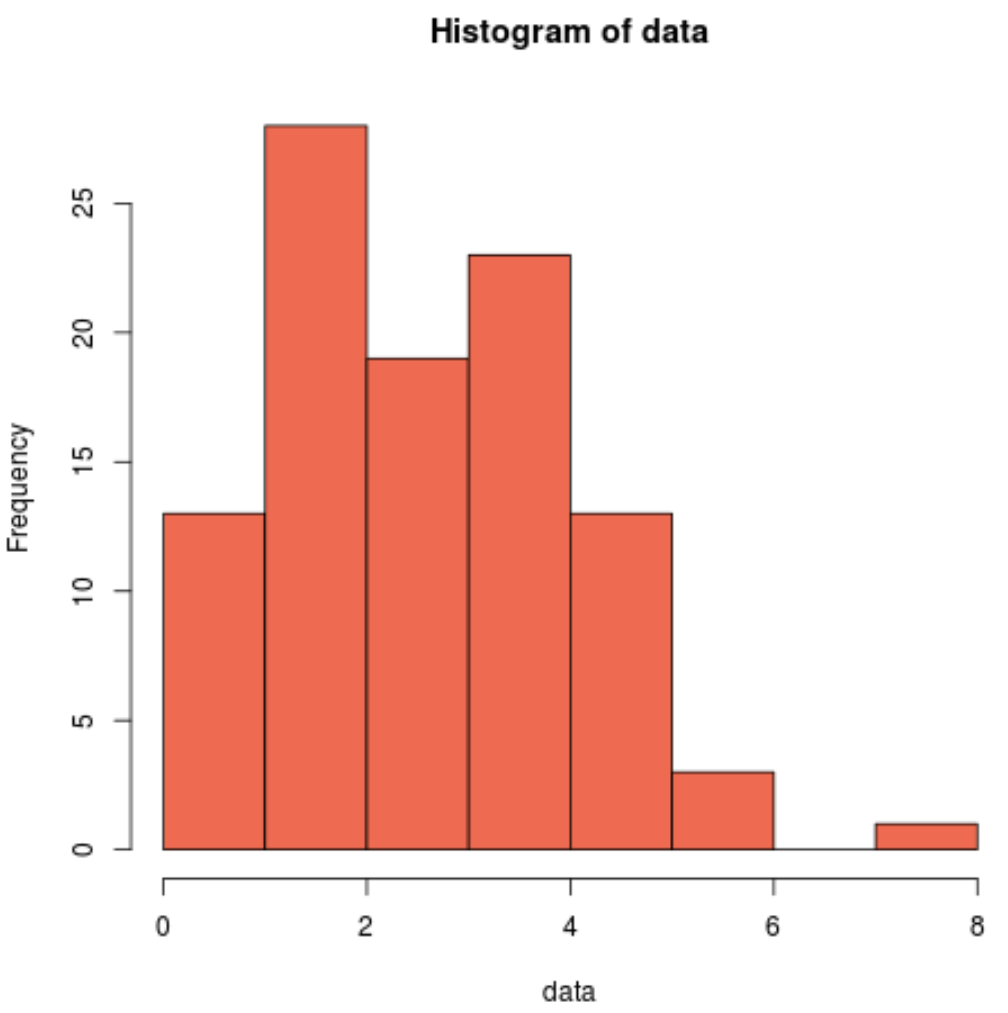
हम देख सकते हैं कि वितरण दाएं-तिरछा है और इसमें सामान्य वितरण से जुड़ा विशिष्ट “घंटी आकार” नहीं है।

इस प्रकार, हमारा हिस्टोग्राम क्रैमर-वॉन मिज़ परीक्षण के परिणामों से मेल खाता है और पुष्टि करता है कि हमारा नमूना डेटा सामान्य वितरण से नहीं आता है।

गैर-सामान्य डेटा का क्या करें

यदि कोई दिया गया डेटा सेट सामान्य रूप से वितरित नहीं है , तो हम इसे अधिक सामान्य बनाने के लिए अक्सर निम्नलिखित परिवर्तनों में से एक कर सकते हैं:

1. लॉग परिवर्तन: प्रतिक्रिया चर को y से log(y) में बदलें।

2. वर्गमूल परिवर्तन: प्रतिक्रिया चर को y से √y में बदलें।

3. घनमूल परिवर्तन: प्रतिक्रिया चर को y से y ^1/3 में बदलें।

इन परिवर्तनों को निष्पादित करके, प्रतिक्रिया चर आम तौर पर सामान्य वितरण का अनुमान लगाता है।

इन परिवर्तनों को व्यवहार में कैसे लाया जाए यह देखने के लिए इस ट्यूटोरियल का संदर्भ लें।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि आर में अन्य सामान्यता परीक्षण कैसे करें:

आर में शापिरो-विल्क परीक्षण कैसे करें
आर में एंडरसन-डार्लिंग परीक्षण कैसे करें
आर में कोलमोगोरोव-स्मिरनोव परीक्षण कैसे करें