घनत्व फंक्शन

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 5, 2023 संभावना शून्य टिप्पणियां

इस लेख में आप जानेंगे कि घनत्व फ़ंक्शन क्या है, घनत्व फ़ंक्शन से संभाव्यता की गणना कैसे की जाती है और इस संभाव्य फ़ंक्शन की विशेषताएं क्या हैं। इसके अतिरिक्त, आप यह देख पाएंगे कि घनत्व फ़ंक्शन और वितरण फ़ंक्शन के बीच क्या अंतर हैं।

घनत्व फलन क्या है?

घनत्व फ़ंक्शन , जिसे संभाव्यता घनत्व फ़ंक्शन भी कहा जाता है, एक गणितीय फ़ंक्शन है जो इस संभावना का वर्णन करता है कि एक निरंतर यादृच्छिक चर एक निश्चित मान लेता है।

दूसरे शब्दों में, एक चर से जुड़ा घनत्व फ़ंक्शन गणितीय रूप से उन संभावनाओं को परिभाषित करता है जो चर एक मान लेता है।

उदाहरण के लिए, मान लें कि आबादी में एक वयस्क व्यक्ति की लंबाई 1.80 मीटर से अधिक होने की संभावना 35% है, तो उक्त संभावना की गणना करते समय घनत्व फ़ंक्शन 35% की संभावना का संकेत देगा।

कभी-कभी संभाव्यता घनत्व फ़ंक्शन को पीडीएफ के रूप में संक्षिप्त किया जाता है।

घनत्व फ़ंक्शन के साथ संभाव्यता की गणना करें

इस संभावना को खोजने के लिए कि एक निरंतर चर एक अंतराल में एक मान लेता है, अंतराल की सीमाओं के बीच उक्त चर से जुड़े घनत्व फ़ंक्शन के अभिन्न अंग की गणना करना आवश्यक है।

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx$

सोना

$f(x)$

सतत यादृच्छिक चर का घनत्व फलन है।

या दूसरे शब्दों में, किसी अंतराल में चर के मान लेने की संभावना उस अंतराल में घनत्व फ़ंक्शन के अंतर्गत आने वाले क्षेत्र के बराबर होती है।

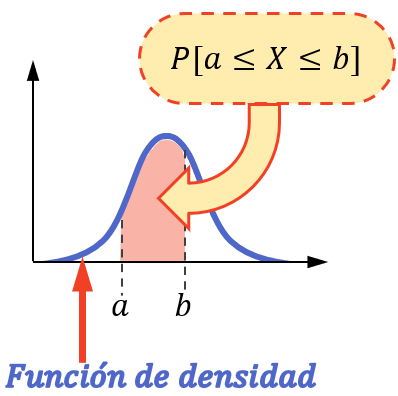
ध्यान दें कि संभाव्यता गणना केवल इस तरह से की जा सकती है यदि सांख्यिकीय चर एक सतत वितरण का अनुसरण करता है, जैसे सामान्य वितरण, घातीय वितरण, पॉइसन वितरण, आदि।

घनत्व फलन के गुण

घनत्व फ़ंक्शन में निम्नलिखित गुण हैं:

x के किसी भी मान के लिए घनत्व फ़ंक्शन का मान शून्य या सकारात्मक है।

$f(x)\geq 0$

इसके अतिरिक्त, घनत्व फ़ंक्शन का अधिकतम मान 1 के बराबर है।

$f(x)\leq 1$

वास्तव में, घनत्व फ़ंक्शन ग्राफ़ के अंतर्गत कुल क्षेत्रफल हमेशा चर की परवाह किए बिना 1 के बराबर होता है, क्योंकि यह सभी संभावनाओं के सेट से मेल खाता है।

$\displaystyle \int_{-\infty}^{+\infty} f(x)dx=1$

जैसा कि पिछले अनुभाग में बताया गया है, एक निरंतर चर के एक अंतराल में एक मान लेने की संभावना की गणना उस अंतराल में घनत्व फ़ंक्शन के अभिन्न अंग के साथ की जाती है।

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx=F(b)-F(a)$

घनत्व फलन और वितरण फलन

इस अंतिम भाग में, हम देखेंगे कि घनत्व फ़ंक्शन और वितरण फ़ंक्शन कैसे भिन्न होते हैं, क्योंकि वे दो प्रकार के संभाव्य फ़ंक्शन हैं जो आम तौर पर भ्रमित होते हैं।

गणितीय रूप से, वितरण फ़ंक्शन घनत्व फ़ंक्शन के अभिन्न अंग के बराबर है , इसलिए वितरण फ़ंक्शन एक सतत चर की संचयी संभावना का वर्णन करता है।

अर्थात्, किसी भी मान के लिए वितरण फ़ंक्शन की छवि इस संभावना के बराबर होती है कि चर उस मान या उससे कम मान लेता है।

इसलिए इन दो प्रकार के कार्यों के बीच गणितीय संबंध इस प्रकार है:

$\displaystyle P[X\leq a]=\int_{-\infty}^a f(x)dx=F(a)$

सोना

$f(x)$

घनत्व फलन है और

$F(x)$

वितरण कार्य है.

ध्यान दें कि घनत्व फ़ंक्शन का ग्राफ़िकल प्रतिनिधित्व एक चर के वितरण फ़ंक्शन के सापेक्ष कैसे बदलता है जो 1 के माध्य और 0.5 के मानक विचलन के साथ सामान्य वितरण का अनुसरण करता है:

वितरण सुविधा के बारे में अधिक जानने के लिए, नीचे दिए गए लिंक पर क्लिक करें:

➤ देखें: वितरण कार्य

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने