चतुर्थक
इस लेख में हम बताते हैं कि चतुर्थक क्या हैं। आपको प्रत्येक चतुर्थक की परिभाषा, उनकी गणना कैसे करें और कई ठोस उदाहरण मिलेंगे। हम आपको यह भी दिखाते हैं कि समूहीकृत डेटा के लिए चतुर्थक की गणना कैसे करें। इसके अतिरिक्त, आप ऑनलाइन कैलकुलेटर से किसी भी डेटा सेट के चतुर्थक की गणना करने में सक्षम होंगे।
चतुर्थक क्या हैं?
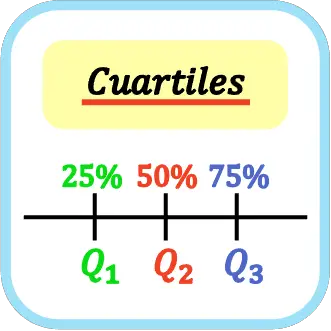
सांख्यिकी में, चतुर्थक वे तीन मान हैं जो क्रमित डेटा के एक सेट को चार बराबर भागों में विभाजित करते हैं। इस प्रकार, पहला, दूसरा और तीसरा चतुर्थक सभी सांख्यिकीय डेटा का क्रमशः 25%, 50% और 75% प्रतिनिधित्व करता है।
चतुर्थक को बड़े Q और चतुर्थक सूचकांक द्वारा दर्शाया जाता है, इसलिए पहला चतुर्थक Q 1 है, दूसरा चतुर्थक Q 2 है, और तीसरा चतुर्थक Q 3 है।
👉 आप किसी भी डेटा सेट के चतुर्थक की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।
यह ध्यान दिया जाना चाहिए कि चतुर्थक, क्विंटाइल, डेसील और प्रतिशतक की तरह ही गैर-केंद्रीय स्थिति का एक माप है। आप इस वेब पेज पर देख सकते हैं कि इनमें से प्रत्येक मात्रा प्रकार क्या है।
प्रथम चतुर्थक
प्रथम चतुर्थक , जिसे चतुर्थक 1 भी कहा जाता है, एक नमूने में सांख्यिकीय डेटा के 25% से अधिक का मान है। दूसरे शब्दों में, पहला चतुर्थक 25% से अधिक देखे गए डेटा का प्रतिनिधित्व करता है।
पहला चतुर्थक प्रतीक Q 1 द्वारा व्यक्त किया गया है और इसका उपयोग नमूने में सबसे छोटे डेटा मानों को दर्शाने के लिए किया जाता है।
दूसरा चतुर्थक
दूसरा चतुर्थक , जिसे चतुर्थक 2 भी कहा जाता है, एक नमूने में सांख्यिकीय डेटा के 50% से अधिक का मान है। इसलिए, दूसरा चतुर्थक डेटा सेट को दो हिस्सों में अलग करता है और माध्यिका और पांचवें दशमलव के साथ मेल खाता है।
दूसरे चतुर्थक का प्रतीक Q2 है।
तृतीय चतुर्थक
तीसरा चतुर्थक , जिसे तीसरा चतुर्थक भी कहा जाता है, वह मान है जो किसी नमूने में सांख्यिकीय डेटा के 75% से अधिक होता है। दूसरे शब्दों में, तीसरा चतुर्थक एकत्र किए गए डेटा का 75% से अधिक प्रतिनिधित्व करता है।
तीसरा चतुर्थक प्रतीक Q 3 द्वारा व्यक्त किया गया है और नमूने में सबसे बड़े मूल्यों का प्रतिनिधित्व करता है।
चतुर्थक की गणना कैसे करें
सांख्यिकीय डेटा सेट के चतुर्थक की स्थिति की गणना करने के लिए, आपको चतुर्थक की संख्या को डेटा की कुल संख्या के योग से एक और गुणा करना होगा और परिणाम को चार से विभाजित करना होगा।
इसलिए चतुर्थक का सूत्र इस प्रकार है:
![]()
कृपया ध्यान दें: यह सूत्र हमें चतुर्थक की स्थिति बताता है, न कि चतुर्थक का मान। चतुर्थक सूत्र द्वारा प्राप्त स्थिति पर स्थित डेटा होगा।
हालाँकि, कभी-कभी इस सूत्र का परिणाम हमें दशमलव संख्या देगा। इसलिए हमें दो मामलों में अंतर करना चाहिए जो इस बात पर निर्भर करता है कि परिणाम दशमलव संख्या है या नहीं:
- यदि सूत्र का परिणाम दशमलव भाग के बिना एक संख्या है, तो चतुर्थक वह डेटा है जो उपरोक्त सूत्र द्वारा प्रदान की गई स्थिति में है।
- यदि सूत्र परिणाम दशमलव भाग वाली एक संख्या है, तो चतुर्थक मान की गणना निम्न सूत्र का उपयोग करके की जाती है:
![]()
जहाँ x i और x i+1 उन स्थितियों की संख्याएँ हैं जिनके बीच पहले सूत्र द्वारा प्राप्त संख्या स्थित है, और d पहले सूत्र द्वारा प्राप्त संख्या का दशमलव भाग है।
अब, हो सकता है कि चतुर्थक की गणना करना आपके लिए बहुत जटिल हो, क्योंकि इसमें बहुत सी बातों को ध्यान में रखना होता है। लेकिन अगले भाग में दो उदाहरणों के साथ, आप देखेंगे कि यह वास्तव में कितना सरल है।
ध्यान दें : वैज्ञानिक समुदाय में, चतुर्थक की गणना कैसे करें, इस पर कोई सहमति नहीं है, इसलिए आप एक सांख्यिकी पुस्तक पा सकते हैं जो इसे थोड़ा अलग तरीके से समझाती है।
चतुर्थक की गणना के उदाहरण
चतुर्थक की गणना कैसे की जाती है, इसे पूरी तरह से समझने के लिए, आपको नीचे दो हल किए गए अभ्यास मिलेंगे। पहले में चतुर्थक पूर्णांक हैं और दूसरे में चतुर्थक दशमलव संख्याएँ हैं, इसलिए आप देख सकते हैं कि आप कौन से दो मामले पा सकते हैं।
उदाहरण 1
- निम्नलिखित डेटा सेट के तीन चतुर्थक की गणना करें:

जैसा कि हमने ऊपर देखा, चतुर्थक निर्धारित करने का सूत्र है:
![]()
इस मामले में n , प्रेक्षणों की कुल संख्या 15 है, इसलिए हमें पहला चतुर्थक ज्ञात करने के लिए n को 15 से और k को 1 से बदलना होगा:
![]()
इसलिए, पहला चतुर्थक मानों की क्रमबद्ध सूची के चौथे स्थान की संख्या है, जो इस मामले में 39 है।
उसी तरह, हम गुणांक k को 2 से प्रतिस्थापित करके दूसरे चतुर्थक की गणना करते हैं:
![]()
इसलिए चतुर्थक 2 क्रमबद्ध सूची में आठवां नंबर है, जो मान 48 से मेल खाता है।
अंत में, हम तीसरे चतुर्थक की गणना के लिए k =3 के साथ आखिरी बार सूत्र लागू करते हैं:
![]()
चतुर्थक 3 बारहवीं स्थिति में डेटा से मेल खाता है, अर्थात 60।
उदाहरण 2
- निम्नलिखित डेटा श्रृंखला के तीन चतुर्थक ज्ञात कीजिए:

इस दूसरे उदाहरण में, हमारे पास 24 अवलोकन हैं, इसलिए चतुर्थक सूत्र से प्राप्त संख्याएँ दशमलव होंगी।
हम पहले सामान्य सूत्र में 1 के स्थान पर k प्रतिस्थापित करके प्रथम चतुर्थक की स्थिति की गणना करते हैं:
![]()
![]()
लेकिन हमें दशमलव संख्या 6.25 मिली, इसलिए पहला चतुर्थक छठे और सातवें डेटा के बीच स्थित है, जो क्रमशः 22 और 25 हैं। इसलिए, सटीक चतुर्थक की गणना करने के लिए हमें निम्नलिखित सूत्र लागू करने की आवश्यकता है:
![]()
इस स्थिति में x i 22 है, x i+1 25 है और d प्राप्त संख्या का दशमलव भाग है, अर्थात 0.25। अभी तक:
![]()
अब हम दूसरा चतुर्थक ज्ञात करने के लिए वही प्रक्रिया अपनाते हैं:
![]()
फिर से हमें सूत्र से एक दशमलव संख्या मिलती है, इस मामले में यह 12.5 है। इसलिए हमें डेटा तालिका में बारहवीं और तेरहवीं संख्याओं के साथ उसी सूत्र का उपयोग करना चाहिए, जो 49 और 50 से मेल खाता है:
![]()
अंत में, हम तीसरा चतुर्थक प्राप्त करने के लिए उसी प्रक्रिया को दोहराते हैं:
![]()
लेकिन संख्या 18.75 संख्या 18 और 19 के बीच है, इसलिए तीसरा चतुर्थक इन पदों के मानों (71 और 73) के बीच होगा। अधिक सटीक रूप से, यह वह मान होगा जो हम निम्नलिखित अभिव्यक्ति से प्राप्त करते हैं:
![]()
चतुर्थक कैलकुलेटर
चतुर्थक की गणना करने के लिए नीचे दिए गए कैलकुलेटर में सांख्यिकीय डेटा सेट प्लग करें। डेटा को एक स्थान से अलग किया जाना चाहिए और दशमलव विभाजक के रूप में अवधि का उपयोग करके दर्ज किया जाना चाहिए।
समूहीकृत डेटा में चतुर्थक
जब डेटा को अंतरालों में समूहीकृत किया जाता है, तो चतुर्थक की गणना करने के लिए, हमें सबसे पहले निम्नलिखित सूत्र का उपयोग करके उस अंतराल या बिन को ढूंढना होगा जिसमें चतुर्थक आता है:
![]()
इसलिए चतुर्थक उस अंतराल में होगा जिसकी पूर्ण संचयी आवृत्ति पिछली अभिव्यक्ति से प्राप्त संख्या से तुरंत अधिक है।
और एक बार जब हम उस अंतराल को जान लेते हैं जिससे चतुर्थक संबंधित है, तो हमें चतुर्थक का सटीक मान ज्ञात करने के लिए निम्नलिखित सूत्र को लागू करना होगा:
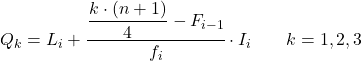
सोना:
- L i उस अंतराल की निचली सीमा है जिसमें चतुर्थक स्थित है।
- n प्रेक्षणों की कुल संख्या है।
- F i-1 पिछले अंतराल की संचयी निरपेक्ष आवृत्ति है।
- f i उस अंतराल की पूर्ण आवृत्ति है जिसमें चतुर्थक स्थित है।
- I i चतुर्थक अंतराल की चौड़ाई है।
उदाहरण के तौर पर, यहां समूहीकृत डेटा की श्रृंखला में चतुर्थक की गणना करने का एक अभ्यास दिया गया है:

प्रथम चतुर्थक की गणना करने के लिए, आपको पहले वह अंतराल निर्धारित करना होगा जिसमें यह आता है। ऐसा करने के लिए, हम निम्नलिखित सूत्र लागू करते हैं:
![]()
![]()
तो पहला चतुर्थक उस अंतराल में होगा जिसकी संचयी निरपेक्ष आवृत्ति तुरंत 7.75 से अधिक है, इस मामले में यह अंतराल [50.60) है जिसकी संचयी निरपेक्ष आवृत्ति 15 है। और एक बार जब हम चतुर्थक अंतराल को जान लेते हैं, तो हम दूसरी प्रक्रिया सूत्र का उपयोग करते हैं :
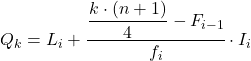
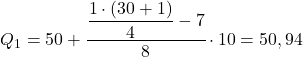
हम दूसरा चतुर्थक प्राप्त करने के लिए फिर से वही प्रक्रिया लागू करते हैं। हम पहले वह अंतराल निर्धारित करते हैं जहां चतुर्थक स्थित है:
![]()
वह अंतराल जिसकी संचयी निरपेक्ष आवृत्ति 15.5 से तुरंत अधिक है [60.70), जिसकी संचयी निरपेक्ष आवृत्ति 26 है। इसलिए दूसरा चतुर्थक है:
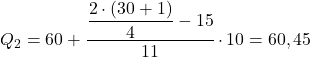
और अंत में, हम तीसरे चतुर्थक को खोजने के लिए प्रक्रिया को दोहराते हैं। हम पहले उस अंतराल की गणना करते हैं जिसमें चतुर्थक शामिल है:
![]()
23.25 के ठीक ऊपर संचयी निरपेक्ष आवृत्ति 26 है, इसलिए तीसरी चतुर्थक सीमा [60.70) है। इसलिए हम इस अंतराल के साथ चतुर्थक की गणना करने के लिए सूत्र लागू करते हैं:
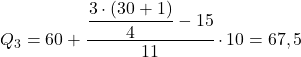
चतुर्थक का उपयोग किस लिए किया जाता है?
चतुर्थक स्थिति का एक माप है, इसलिए उनका उपयोग यह जानने के लिए किया जाता है कि डेटा की स्थिति कैसे है। दूसरे शब्दों में, तीन चतुर्थक के मान हमें यह जानने की अनुमति देते हैं कि नमूने में एक यादृच्छिक डेटा आइटम बहुत बड़ा है, बहुत छोटा है या यदि यह औसत मूल्य है।
यदि हम नमूने से बेतरतीब ढंग से डेटा का एक टुकड़ा लेते हैं, तो हम इसकी चतुर्थक से तुलना करके बता सकते हैं कि इसका मूल्य उच्च या निम्न है। यदि यादृच्छिक डेटा मान पहले चतुर्थक से कम है, तो यह एक छोटा मान होगा, लेकिन यदि इसका मान तीसरे चतुर्थक से अधिक है, तो यह एक बड़ा मान होगा। इसी तरह, यदि उक्त डेटा का मान पहले और तीसरे चतुर्थक के बीच है, तो यह एक मध्यवर्ती मान है।
दूसरी ओर, चतुर्थक का उपयोग अन्य सांख्यिकीय उपायों की गणना करने के लिए भी किया जाता है, जैसे कि इंटरक्वेर्टाइल रेंज (या इंटरक्वेर्टाइल रेंज), और आरेख बनाने के लिए, जैसे कि बॉक्स और व्हिस्कर प्लॉट (या बॉक्सप्लॉट)।