ची स्क्वायर डिस्ट्रीब्यूशन टेबल कैसे पढ़ें

यह ट्यूटोरियल बताता है कि ची-स्क्वायर वितरण चार्ट को कैसे पढ़ें और व्याख्या करें।

ची वर्ग वितरण तालिका क्या है?

ची-स्क्वायर वितरण तालिका एक तालिका है जो ची-स्क्वायर वितरण के महत्वपूर्ण मूल्यों को दर्शाती है। ची-स्क्वायर वितरण तालिका का उपयोग करने के लिए, आपको केवल दो मान जानने की आवश्यकता है:

• ची स्क्वायर परीक्षण के लिए स्वतंत्रता की डिग्री
• परीक्षण का अल्फा स्तर (सामान्य विकल्प 0.01, 0.05 और 0.10 हैं)

निम्नलिखित छवि ची-स्क्वायर वितरण तालिका की पहली 20 पंक्तियों को दिखाती है, जिसमें तालिका के बाईं ओर स्वतंत्रता की डिग्री और तालिका के शीर्ष पर अल्फा स्तर हैं:

नोट: आप यहां स्वतंत्रता की अधिक डिग्री के साथ पूर्ण ची-स्क्वायर वितरण तालिका पा सकते हैं।

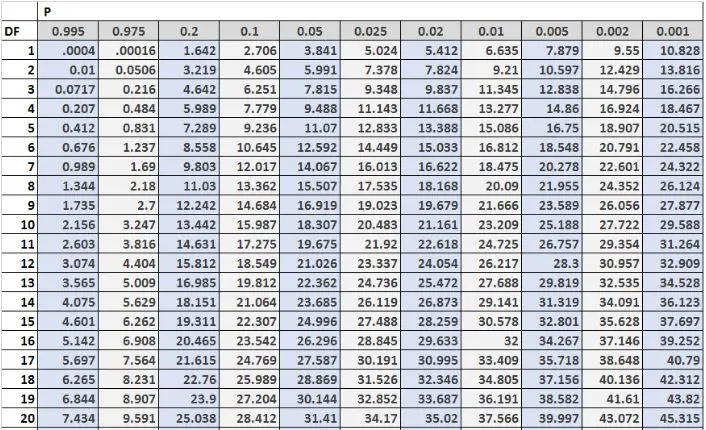
तालिका में महत्वपूर्ण मानों की तुलना अक्सर ची-स्क्वायर परीक्षण के परीक्षण आँकड़ों से की जाती है। यदि परीक्षण आँकड़ा तालिका में पाए गए महत्वपूर्ण मान से अधिक है, तो आप ची-स्क्वायर परीक्षण की शून्य परिकल्पना को अस्वीकार कर सकते हैं और निष्कर्ष निकाल सकते हैं कि परीक्षण के परिणाम सांख्यिकीय रूप से महत्वपूर्ण हैं।

ची-स्क्वायर वितरण तालिका का उपयोग करने के उदाहरण

हम दिखाएंगे कि निम्नलिखित तीन प्रकार के ची-स्क्वायर परीक्षणों के साथ ची-स्क्वायर वितरण तालिका का उपयोग कैसे करें:

• स्वतंत्रता के लिए काई-स्क्वायर परीक्षण
• फिट की अच्छाई के लिए ची-स्क्वायर परीक्षण
• समरूपता के लिए काई-स्क्वायर परीक्षण

स्वतंत्रता के लिए काई-स्क्वायर परीक्षण

हम स्वतंत्रता के लिए ची-स्क्वायर परीक्षण का उपयोग करते हैं जब हम यह परीक्षण करना चाहते हैं कि दो श्रेणीगत चरों के बीच कोई महत्वपूर्ण संबंध है या नहीं।

उदाहरण: मान लीजिए कि हम जानना चाहते हैं कि किसी राजनीतिक दल की प्राथमिकता के साथ लिंग का संबंध है या नहीं। हम 500 मतदाताओं का एक सरल यादृच्छिक नमूना लेते हैं और उनसे उनकी राजनीतिक पार्टी की पसंद के बारे में पूछते हैं। 0.05 के महत्व स्तर का उपयोग करते हुए, हम यह निर्धारित करने के लिए एक ची-स्क्वायर परीक्षण करते हैं कि लिंग राजनीतिक दल की प्राथमिकता से जुड़ा है या नहीं। निम्नलिखित तालिका सर्वेक्षण के परिणाम प्रस्तुत करती है:

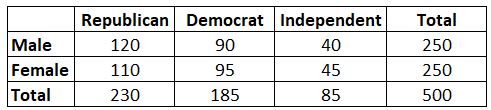
यह पता चला है कि इस ची-स्क्वायर परीक्षण के लिए परीक्षण आँकड़ा 0.864 है।

फिर हम ची वर्ग वितरण तालिका में महत्वपूर्ण परीक्षण मान पा सकते हैं। स्वतंत्रता की डिग्री (#पंक्तियाँ-1) * (#कॉलम-1) = (2-1) * (3-1) = 2 के बराबर हैं और समस्या ने हमें बताया कि हमें 0.05 के अल्फा स्तर का उपयोग करना चाहिए, ची-स्क्वायर वितरण तालिका के अनुसार, परीक्षण का महत्वपूर्ण मूल्य 5.991 है।

चूँकि हमारा परीक्षण आँकड़ा हमारे महत्वपूर्ण मान से कम है, हम शून्य परिकल्पना को अस्वीकार करने में विफल रहते हैं। इसका मतलब यह है कि हमारे पास यह कहने के लिए पर्याप्त सबूत नहीं हैं कि लिंग और राजनीतिक दल की प्राथमिकताओं के बीच कोई संबंध है।

फिट की अच्छाई के लिए ची-स्क्वायर परीक्षण

जब हम यह परीक्षण करना चाहते हैं कि कोई श्रेणीबद्ध चर एक काल्पनिक वितरण का पालन करता है या नहीं, तो हम ची-स्क्वायर गुडनेस-ऑफ-फिट परीक्षण का उपयोग करते हैं।

उदाहरण: एक स्टोर मालिक का कहना है कि उसके सभी सप्ताहांत ग्राहकों में से 30% शुक्रवार को, 50% शनिवार को और 20% रविवार को आते हैं। एक स्वतंत्र शोधकर्ता यादृच्छिक सप्ताहांत पर स्टोर पर जाता है और शुक्रवार को 91, शनिवार को 104 और रविवार को 65 ग्राहक पाता है। 0.10 के महत्व स्तर का उपयोग करते हुए, हम यह निर्धारित करने के लिए फिट की अच्छाई की जांच करने के लिए एक ची-स्क्वायर परीक्षण करते हैं कि डेटा स्टोर मालिक के दावे के अनुरूप है या नहीं।

इस मामले में, परीक्षण आँकड़ा 10,616 निकला।

फिर हम ची वर्ग वितरण तालिका में महत्वपूर्ण परीक्षण मान पा सकते हैं। स्वतंत्रता की डिग्री (#परिणाम-1) = 3-1 = 2 के बराबर है और समस्या हमें बताती है कि हमें 0.10 के अल्फा स्तर का उपयोग करना चाहिए। तो, ची-स्क्वायर वितरण तालिका के अनुसार, परीक्षण का महत्वपूर्ण मूल्य 4.605 है।

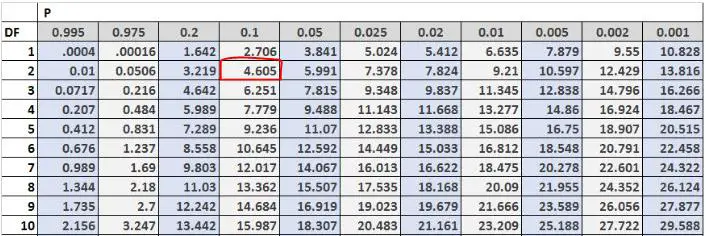
चूँकि हमारा परीक्षण आँकड़ा हमारे महत्वपूर्ण मान से अधिक है, हम शून्य परिकल्पना को अस्वीकार करते हैं। इसका मतलब यह है कि हमारे पास यह कहने के लिए पर्याप्त सबूत हैं कि सप्ताहांत में इस स्टोर पर आने वाले ग्राहकों का वास्तविक वितरण शुक्रवार को 30%, शनिवार को 50% और रविवार को 20% के बराबर नहीं है।

समरूपता के लिए काई-स्क्वायर परीक्षण

हम समरूपता के लिए ची-स्क्वायर परीक्षण का उपयोग करते हैं जब हम औपचारिक रूप से परीक्षण करना चाहते हैं कि कई समूहों के बीच अनुपात में अंतर है या नहीं।

उदाहरण: एक बास्केटबॉल प्रशिक्षण केंद्र यह देखना चाहता है कि क्या दो नए प्रशिक्षण कार्यक्रमों से कठिन शूटिंग टेस्ट पास करने वाले उसके खिलाड़ियों के अनुपात में सुधार होता है। 172 खिलाड़ियों को प्रोग्राम 1, 173 को प्रोग्राम 2, और 215 को वर्तमान प्रोग्राम के लिए यादृच्छिक रूप से सौंपा गया है। एक महीने तक प्रशिक्षण कार्यक्रमों का उपयोग करने के बाद, खिलाड़ी शूटिंग परीक्षण लेते हैं। नीचे दी गई तालिका उन खिलाड़ियों की संख्या दर्शाती है जो उनके द्वारा उपयोग किए गए प्रोग्राम के आधार पर शूटिंग टेस्ट पास करते हैं।

0.05 के महत्व स्तर का उपयोग करते हुए, हम यह निर्धारित करने के लिए एक ची-स्क्वायर परीक्षण करते हैं कि प्रत्येक प्रशिक्षण कार्यक्रम के लिए सफलता दर समान है या नहीं।

यह पता चला है कि इस ची-स्क्वायर परीक्षण का परीक्षण आँकड़ा 4.208 है।

फिर हम ची वर्ग वितरण तालिका में महत्वपूर्ण परीक्षण मान पा सकते हैं। स्वतंत्रता की डिग्री (#पंक्तियाँ-1) * (#कॉलम-1) = (2-1) * (3-1) = 2 के बराबर हैं और समस्या ने हमें बताया कि हमें 0.05 के अल्फा स्तर का उपयोग करना चाहिए, ची-स्क्वायर वितरण तालिका के अनुसार, परीक्षण का महत्वपूर्ण मूल्य 5.991 है।

चूँकि हमारा परीक्षण आँकड़ा हमारे महत्वपूर्ण मान से कम है, हम शून्य परिकल्पना को अस्वीकार करने में विफल रहते हैं। इसका मतलब यह है कि हमारे पास यह कहने के लिए पर्याप्त सबूत नहीं हैं कि तीन प्रशिक्षण कार्यक्रम अलग-अलग परिणाम देते हैं।