ज्यामितीय साधन

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 6, 2023 आंकड़े शून्य टिप्पणियां

इस लेख में हम बताते हैं कि ज्यामितीय माध्य क्या है, इसकी गणना कैसे की जाती है और ज्यामितीय माध्य और अंकगणितीय माध्य के बीच क्या अंतर है। आप ज्यामितीय माध्य के चरण-दर-चरण हल किए गए अभ्यास को भी देख पाएंगे और इस प्रकार के माध्य के गुण क्या हैं। अंत में, आपको किसी भी डेटा सेट के ज्यामितीय माध्य की गणना करने के लिए एक कैलकुलेटर मिलेगा।

ज्यामितीय माध्य क्या है?

ज्यामितीय माध्य वर्णनात्मक आँकड़ों की केंद्रीयता का एक माप है। सांख्यिकीय डेटा के एक सेट का ज्यामितीय माध्य सभी मूल्यों के उत्पाद के nवें मूल के बराबर है।

ज्यामितीय माध्य का उपयोग व्यवसाय वित्त में रिटर्न की दरों, प्रतिशत औसत और चक्रवृद्धि ब्याज की गणना के लिए किया जाता है।

इसलिए ज्यामितीय माध्य का सूत्र इस प्रकार है:

ज्यामितीय माध्य की गणना केवल तभी की जा सकती है जब नमूने में सभी डेटा सकारात्मक हो। क्योंकि यदि कोई मान ऋणात्मक है, तो मूल का ऋणात्मक समाधान होगा या कोई समाधान नहीं होगा, दूसरी ओर, यदि कोई डेटा शून्य है तो डेटा का गुणन शून्य देगा और इसलिए, ज्यामितीय माध्य 0 के बराबर होगा।

ज्यामितीय माध्य एकमात्र प्रकार का माध्य नहीं है जो मौजूद है, अंकगणितीय माध्य, भारित माध्य, वर्ग माध्य और हार्मोनिक माध्य भी है।

ज्यामितीय माध्य और अंकगणितीय माध्य के बीच अंतर

ज्यामितीय माध्य और अंकगणितीय माध्य के बीच मुख्य अंतर यह है कि ज्यामितीय माध्य अंकगणितीय माध्य की तुलना में चरम मूल्यों के प्रति कम संवेदनशील होता है। इसके अतिरिक्त, अंकगणितीय माध्य की गणना नकारात्मक और शून्य मानों के साथ की जा सकती है, जबकि ज्यामितीय माध्य की गणना केवल सकारात्मक मानों के साथ की जा सकती है।

इसी तरह, समान डेटा सेट के लिए ज्यामितीय माध्य आम तौर पर अंकगणितीय माध्य से कम होगा।

यह भी ध्यान दिया जाना चाहिए कि ज्यामितीय माध्य की गणना अधिक जटिल है और इसलिए इसके सांख्यिकीय महत्व की व्याख्या करना अधिक कठिन है।

संक्षेप में, अंकगणितीय औसत की तुलना में ज्यामितीय औसत के फायदे और नुकसान हैं और, डेटा की प्रकृति के आधार पर, इस या उस औसत की गणना करना उचित होगा।

ज्यामितीय माध्य की गणना कैसे करें

ज्यामितीय माध्य की गणना करने के लिए, निम्नलिखित चरणों का पालन किया जाना चाहिए:

नमूने में सभी सांख्यिकीय डेटा के उत्पाद की गणना करें।
परिकलित उत्पाद का nवाँ मूल ज्ञात कीजिए।
प्राप्त परिणाम सांख्यिकीय नमूने का ज्यामितीय माध्य है।

जैसा कि आप देख सकते हैं, कैलकुलेटर या कंप्यूटर प्रोग्राम के साथ डेटा के एक सेट का ज्यामितीय माध्य ढूंढना अपेक्षाकृत सरल है, क्योंकि आपको केवल एक उत्पाद और एक रूट की गणना करने की आवश्यकता है। इसके विपरीत, हाथ से गणना करना काफी श्रमसाध्य है।

👉 यही कारण है कि हम डेटा सेट के ज्यामितीय माध्य की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग करने की सलाह देते हैं।

ज्यामितीय माध्य उदाहरण

एक बार जब हम ज्यामितीय माध्य के बारे में सिद्धांत देख लेंगे, तो हम एक उदाहरण देंगे ताकि आप देख सकें कि ज्यामितीय माध्य कैसे प्राप्त किया जाए।

किसी कंपनी के पिछले पांच वर्षों के आर्थिक नतीजे ज्ञात होते हैं। पहले वर्ष में कंपनी ने 10% की आर्थिक लाभप्रदता अर्जित की, दूसरे वर्ष में लाभ 23% तक पहुंच गया, तीसरे वर्ष में अर्जित धन 16% था, चौथे वर्ष में इसने 7% की आर्थिक लाभप्रदता और निवेश हासिल किया पांचवें वर्ष में 20% का रिटर्न दर्शाया गया। आपसे सभी प्रतिशतों का औसत निकालने के लिए कहा जाता है।

जैसा कि हमने देखा, प्रतिशत के औसत की गणना करने के लिए, आपको अंकगणितीय औसत का उपयोग नहीं करना चाहिए, बल्कि ज्यामितीय औसत के साथ गणना करनी चाहिए।

इसलिए, हम ज्यामितीय माध्य सूत्र लागू करते हैं:

$MG=\sqrt[n]{\prod_{i=1}^Nx_i}=\sqrt[n]{x_1\cdot x_2\cdot \ldots x_n}$

और हम उदाहरण मानों को सूत्र में प्रतिस्थापित करते हैं और गणना करते हैं:

$MG=\sqrt[5]{1,10\cdot 1,23\cdot 1,16\cdot 1,07\cdot 1,20}=1,15 \ \longrightarrow \ 15 \%$

ध्यान दें कि हमारे पास पाँच डेटा बिंदु हैं, इसलिए हम पाँचवें मूल की गणना कर रहे हैं।

ज्यामितीय माध्य का संख्यात्मक परिणाम 1.15 है, जिसका अर्थ है कि कंपनी ने हर साल औसतन 15% की आर्थिक वृद्धि का अनुभव किया।

ध्यान रखें कि हम ज्यामितीय माध्य प्राप्त करने में सक्षम थे क्योंकि सभी मान सकारात्मक थे, लेकिन यदि कोई प्रतिशत नकारात्मक होता तो हमें डेटा को पूर्णांक भाग के साथ सकारात्मक दशमलव के रूप में सूत्र में रखना होता। शून्य के बराबर. उदाहरण के लिए, -30% की वृद्धि को सूत्र में 0.70 (1-0.3=0.7) के रूप में व्यक्त किया जाना चाहिए।

ज्यामितीय माध्य कैलकुलेटर

किसी भी नमूना आँकड़े का ज्यामितीय माध्य ज्ञात करने के लिए उसे नीचे दिए गए कैलकुलेटर में प्लग करें। डेटा को एक स्थान से अलग किया जाना चाहिए और दशमलव विभाजक के रूप में अवधि का उपयोग करके दर्ज किया जाना चाहिए। याद रखें कि यदि कोई मान ऋणात्मक या शून्य है तो आप ज्यामितीय माध्य निर्धारित नहीं कर सकते।

ज्यामितीय माध्य के गुण

ज्यामितीय माध्य में निम्नलिखित विशेषताएं हैं:

यह एक प्रकार का औसत है जो प्रतिशत या सूचकांकों का औसत निकालने के लिए बहुत उपयोगी है।

इसकी गणना केवल तभी की जा सकती है जब सभी डेटा सकारात्मक हों।

दो संख्याओं a और b के ज्यामितीय माध्य का ज्यामितीय अर्थ एक वर्ग की भुजा है जिसका क्षेत्रफल उस आयत के समान है जिसकी भुजाएँ a और b मापती हैं।

$MG(a,b)=\sqrt{a\cdot b}$

तीन संख्याओं a , b और c के ज्यामितीय माध्य का ज्यामितीय अर्थ एक घन की भुजा है जिसका आयतन भुजाओं a , b और c के समांतर चतुर्भुज के बराबर है।

$MG(a,b,c)=\sqrt[3]{a\cdot b \cdot c}$

डेटा के एक सेट के ज्यामितीय माध्य का लघुगणक उसी सेट के लघुगणक का अंकगणितीय माध्य देता है।

मानों के समूह का ज्यामितीय माध्य हमेशा अंकगणितीय माध्य से कम या उसके बराबर होगा।

$\sqrt[N]{x_1\cdot x_2\ldots x_N}\leq \cfrac{x_1+x_2+\ldots+x_N}{N}$

भारित ज्यामितीय माध्य की गणना ज्यामितीय माध्य की तरह ही की जाती है, लेकिन सांख्यिकीय मूल्यों को भारित करने के लिए प्रत्येक डेटा आइटम के घातांक में भार जोड़कर।

$\displaystyle \left(\prod_{i=1}^n{x_i}^{\alpha_i}\right)^{\frac{1}{\sum_i{\alpha_i}}}= \left({x_1}^{\alpha_1}{x_2}^{\alpha_2}\dots{x_n}^{\alpha_n}\right)^{ \frac{1}{\alpha_1+ \dots+ \alpha_n}} \left}}$

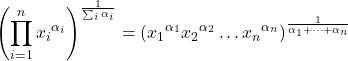
एक्सेल में ज्यामितीय माध्य की गणना करें

अंत में, आइए देखें कि एक्सेल प्रोग्राम का उपयोग करके डेटा सेट का ज्यामितीय माध्य कैसे खोजा जाए।

एक्सेल में ज्यामितीय माध्य की गणना करने के लिए, आपको MEANS.GEOM फ़ंक्शन का उपयोग करना होगा। बस वे सभी मान दर्ज करें जिनका आप ज्यामितीय माध्य लेना चाहते हैं और फ़ंक्शन ज्यामितीय माध्य परिणाम लौटा देगा।

उदाहरण के लिए, ऊपर दिए गए उदाहरण का ज्यामितीय माध्य निर्धारित करने के लिए, आपको एक्सेल बॉक्स में लिखना होगा =MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20) ।

आपको यह ध्यान रखना चाहिए कि यदि कोई भी मान शून्य या नकारात्मक है, तो फ़ंक्शन एक त्रुटि लौटाएगा।

जैसा कि आप देख सकते हैं, एक्सेल के साथ ज्यामितीय माध्य की गणना करना बहुत आसान और तेज़ है, क्योंकि आपको बस डेटा को एक शीट पर कॉपी करना होगा और एक सूत्र का उपयोग करना होगा।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने