सहप्रसरण आव्यूह

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 5, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि सहप्रसरण मैट्रिक्स क्या है और इसका सूत्र क्या है। आप एक ठोस उदाहरण और सहप्रसरण मैट्रिक्स के गुणों के साथ सहप्रसरण मैट्रिक्स बनाने का तरीका जानेंगे।

सहप्रसरण मैट्रिक्स क्या है?

सहप्रसरण मैट्रिक्स एक वर्ग मैट्रिक्स है जिसके तत्व अध्ययन किए गए चर के प्रसरण और सहप्रसरण हैं। इस प्रकार, सहप्रसरण मैट्रिक्स के मुख्य विकर्ण के तत्व प्रत्येक चर के प्रसरण हैं, और शेष तत्व चर के बीच सहप्रसरण हैं।

आंकड़ों में, सहप्रसरण मैट्रिक्स का उपयोग दो या दो से अधिक यादृच्छिक चर के बीच संबंध का विश्लेषण करने के लिए किया जाता है। सहप्रसरण मैट्रिक्स बहुत उपयोगी है क्योंकि यह आपको कई चरों के बीच सहसंबंध की त्वरित व्याख्या करने की अनुमति देता है, क्योंकि आप एक ही समय में चर के सभी सहप्रसरणों के मान देख सकते हैं।

सहप्रसरण मैट्रिक्स का प्रतीक बड़ा ग्रीक अक्षर सिग्मा (Σ) है।

सहप्रसरण मैट्रिक्स की गणना कैसे करें

कई सांख्यिकीय चरों के सहप्रसरण मैट्रिक्स की गणना करने के लिए, निम्नलिखित चरणों का पालन किया जाना चाहिए:

सभी चरों के प्रसरणों की गणना करें।
चरों के प्रत्येक जोड़े के सहप्रसरण की गणना करें।
सहप्रसरण मैट्रिक्स बनाएं:

वेरिएबल i का विचरण मैट्रिक्स के मुख्य विकर्ण पर रखा जाना चाहिए, अधिक सटीक रूप से स्थिति i,i में।
चर i और j के बीच सहप्रसरण को मैट्रिक्स की स्थिति i,j में रखा जाना चाहिए।

इसलिए सहप्रसरण मैट्रिक्स का सूत्र इस प्रकार है:

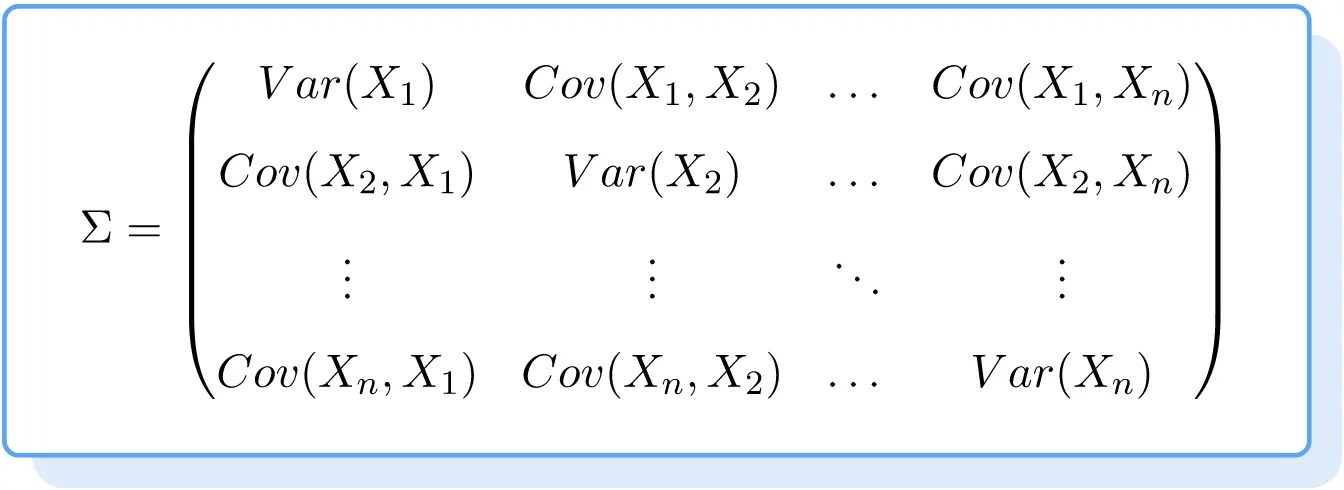
सहप्रसरण मैट्रिक्स उदाहरण

सहप्रसरण मैट्रिक्स की परिभाषा देखने के बाद, नीचे चरण-दर-चरण अभ्यास दिया गया है ताकि आप देख सकें कि इस प्रकार का मैट्रिक्स कैसे बनाया जाता है।

चर X, Y और Z के सहप्रसरण मैट्रिक्स की गणना करता है, जिनके मान हैं:

एक्स: 4, 7, 12, 5, 7
और: 9, 15, 19, 6, 8
जेड: 7, 2, 4, 6, 3

पहली चीज़ जो हमें करने की ज़रूरत है वह सभी चरों के प्रसरणों को निर्धारित करना है:

$Var(X)=7,6$

$Var(Y)=23,44$

$Var(Z)=3,44$

➤ देखें: गैप कैलकुलेटर

दूसरा, हम चरों के प्रत्येक जोड़े के बीच सहप्रसरण पाते हैं:

$Cov(X,Y)=11,2$

$Cov(X,Z)=-2,6$

$Cov(Y,Z)=-4,36$

➤ देखें: सहप्रसरण कैलकुलेटर

और एक बार जब हम सभी प्रसरणों और सहप्रसरणों की गणना कर लेते हैं, तो केवल सहप्रसरण मैट्रिक्स बनाना ही शेष रह जाता है। ऐसा करने के लिए, हम विचरण मानों को मैट्रिक्स के मुख्य विकर्ण पर और सहप्रसरण मानों को उनकी संगत स्थिति में रखते हैं:

$\Sigma=\begin{pmatrix}Var(X)&Cov(X,Y)&Cov(X,Z)\\[1.5ex]Cov(Y,X)&Var(Y)&Cov(Y,Z)\\[1.5ex]Cov(Z,X)&Cov(Z,Y)&Var(Z)\end{pmatrix}$

$\Sigma=\begin{pmatrix}7,6&11,2&-2,6\\[1.5ex]11,2&23,44&-4,36\\[1.5ex]-2,6&-4,36&3,44\end{pmatrix}$

जैसा कि आप देख सकते हैं, एक मैट्रिक्स में भिन्नताओं और सहप्रसरणों का प्रतिनिधित्व करके, चरों की व्याख्या करना बहुत आसान है। सबसे बड़े फैलाव वाला चर Y (23.44) है, दूसरी ओर चर X और Y का सीधा संबंध है, जबकि चर X और Z (और इसलिए Y और Z) का विपरीत संबंध है।

ध्यान दें कि सहप्रसरण मैट्रिक्स हमेशा सममित होता है, क्योंकि दो चर के बीच का सहप्रसरण चर के क्रम पर निर्भर नहीं करता है। उदाहरण के लिए,

$Cov(X,Y)$

के बराबर है

$Cov(Y,X).$

इसके अतिरिक्त, सहप्रसरण मैट्रिक्स हमेशा एक वर्ग मैट्रिक्स होगा और इसका आयाम चर की संख्या के बराबर होगा। इस मामले में हमारे पास तीन चर थे और इसीलिए यह एक 3×3 मैट्रिक्स है, लेकिन यदि हमारे पास केवल दो चर होते तो सहप्रसरण मैट्रिक्स 2×2 होता।

सहप्रसरण मैट्रिक्स के गुण

सहप्रसरण मैट्रिक्स में निम्नलिखित विशेषताएं हैं:

सहप्रसरण मैट्रिक्स चरों की संख्या के क्रम का एक वर्ग मैट्रिक्स है।
सहप्रसरण मैट्रिक्स सममित है, जिसका अर्थ है कि मैट्रिक्स का मुख्य विकर्ण समरूपता का अक्ष है।
सहप्रसरण मैट्रिक्स हमेशा सकारात्मक अर्ध-निश्चित होता है।
सहप्रसरण मैट्रिक्स का निर्धारक शून्य के बराबर या उससे अधिक है।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने