एक्सेल: दो डेटा सेट की एक सांख्यिकीय तुलना बनाएं

अक्सर, आप यह समझने के लिए एक्सेल में दो डेटा सेटों की सांख्यिकीय तुलना करना चाह सकते हैं कि प्रत्येक डेटा सेट में मूल्यों का वितरण कैसे भिन्न होता है।

सांख्यिकीय तुलना करने के दो सामान्य तरीके हैं:

विधि 1: प्रत्येक डेटा सेट के पांच अंकों के सारांश की गणना करें

हम प्रत्येक डेटा सेट के पांच-संख्या सारांश की गणना कर सकते हैं, जिसमें निम्नलिखित मान शामिल हैं:

• न्यूनतम मूल्य
• प्रथम चतुर्थक (25वाँ प्रतिशतक)
• माध्यिका (50वाँ प्रतिशतक)
• तीसरा चतुर्थक (75वाँ प्रतिशतक)
• अधिकतम

इन पांच मूल्यों की गणना करके, हम प्रत्येक डेटा सेट में मूल्यों के वितरण की अच्छी समझ प्राप्त कर सकते हैं।

विधि 2: माध्य और मानक विचलन की गणना करें

दो डेटा सेटों की सांख्यिकीय तुलना करने का एक आसान तरीका प्रत्येक डेटा सेट के माध्य और मानक विचलन की गणना करना है।

इससे हमें यह समझने में मदद मिलती है कि “केंद्रीय” मान कहां है और प्रत्येक डेटा सेट में मूल्यों का वितरण क्या है।

निम्नलिखित उदाहरण दिखाता है कि व्यवहार में इनमें से प्रत्येक विधि का उपयोग कैसे करें।

उदाहरण: एक्सेल में डेटा के दो सेटों की सांख्यिकीय तुलना करें

मान लीजिए कि हमारे पास एक्सेल में डेटा के दो सेट हैं जो एक विशेष परीक्षा में प्राप्त दो अलग-अलग कक्षाओं के छात्रों के परिणाम दिखाते हैं:

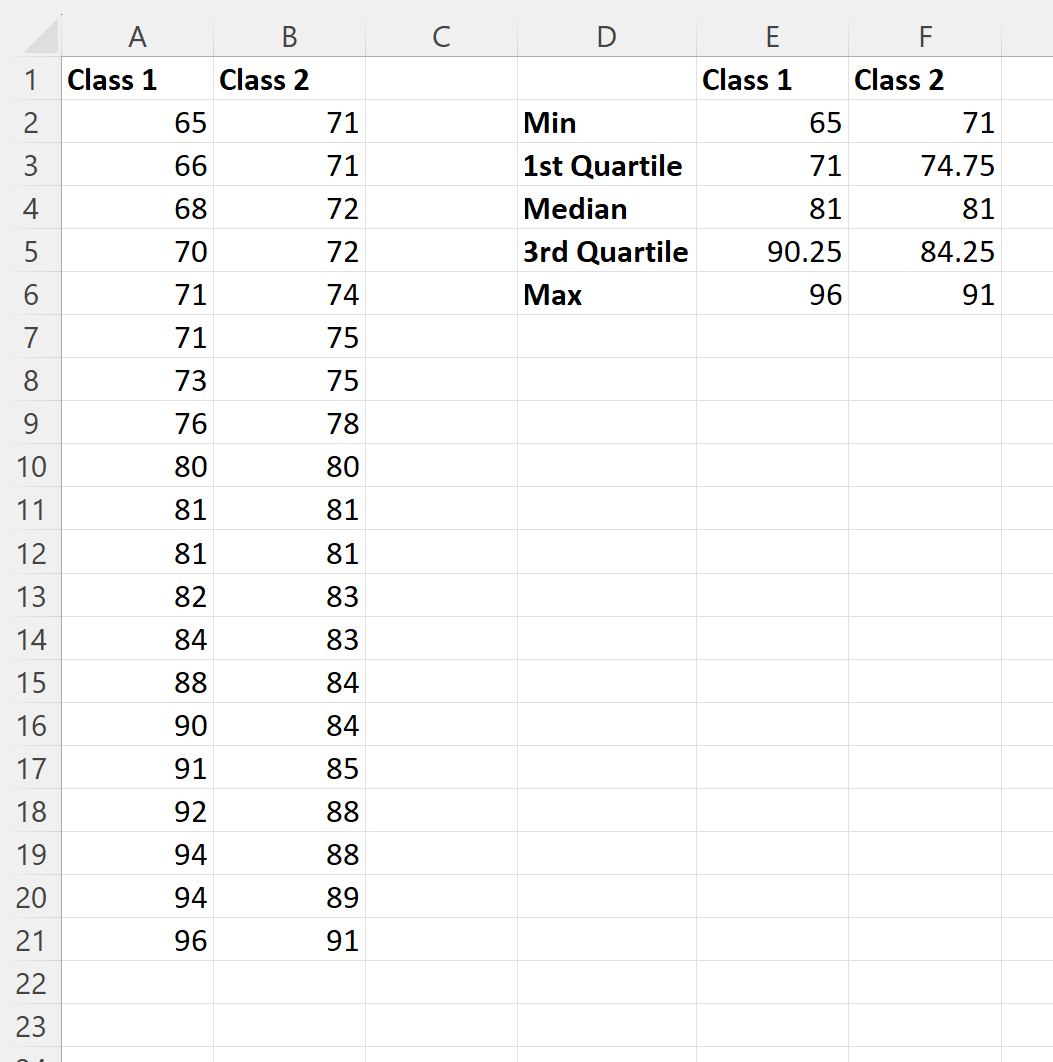
हम कक्षा 1 के परीक्षा परिणामों के पांच अंकों के सारांश की गणना करने के लिए कॉलम ई की कोशिकाओं में निम्नलिखित सूत्र टाइप कर सकते हैं:

• E2 : =MIN(A2:A21)
• E3 : =चतुर्थक(A2:A21, 1)
• E4 : =माध्यिका(A2:A21)
• E5 : =चतुर्थक(A2:A21, 3)
• E6 : =MAX(A2:A21

फिर हम कक्षा 2 के लिए समान मानों की गणना करने के लिए इन सूत्रों को क्लिक करके दाईं ओर खींच सकते हैं:

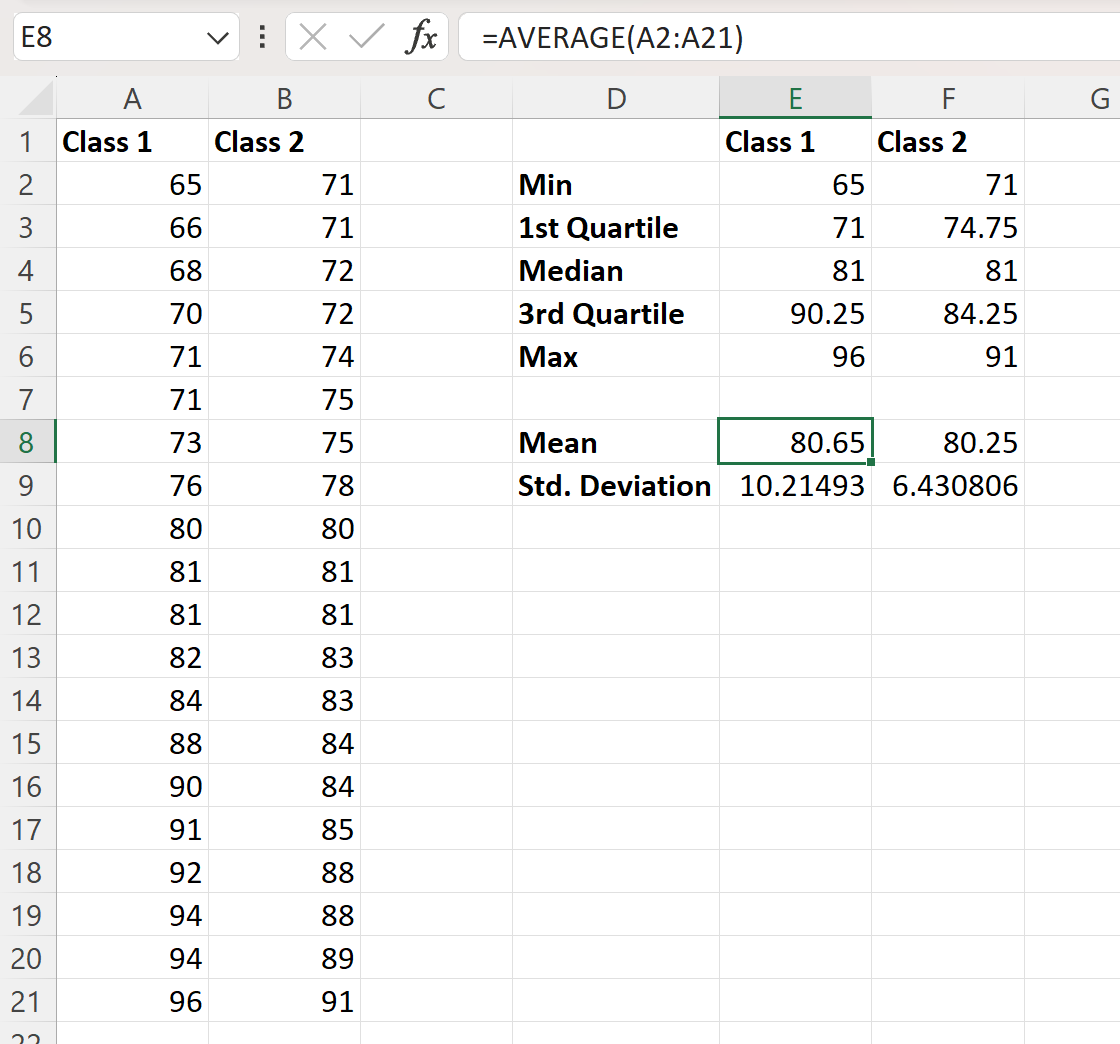
फिर हम कक्षा 1 के परीक्षा परिणामों के माध्य और मानक विचलन की गणना करने के लिए कॉलम ई की कोशिकाओं में निम्नलिखित सूत्र दर्ज कर सकते हैं:

• E8 : =औसत(A2:A21)
• E9 : =ETDEV(A2:A21, 1)

फिर हम कक्षा 2 के लिए समान मानों की गणना करने के लिए इन सूत्रों को क्लिक करके दाईं ओर खींच सकते हैं:

हम दो डेटा सेटों की इस सांख्यिकीय तुलना से निम्नलिखित निष्कर्ष निकाल सकते हैं:

निष्कर्ष 1: दोनों डेटासेट का “मुख्य” मान समान है।

दोनों डेटासेट का औसत परीक्षा स्कोर 81 है। औसत मान केवल थोड़ा भिन्न हैं: प्रथम श्रेणी का औसत परीक्षा स्कोर 80.65 है जबकि दूसरी कक्षा का औसत परीक्षा स्कोर 80.65 है जबकि दूसरी कक्षा का औसत परीक्षा स्कोर है। 80.65′ 80.25 की समीक्षा।

यह हमें बताता है कि दोनों वर्गों के बीच “मुख्य” या “विशिष्ट” परीक्षा स्कोर समान है।

निष्कर्ष 2: पहले डेटा सेट में मूल्यों का बहुत बड़ा “फैलाव” है।

कई संकेतक हमें बताते हैं कि पहली कक्षा के परीक्षा परिणाम दूसरी कक्षा की तुलना में कहीं अधिक बिखरे हुए होते हैं।

उदाहरण के लिए, कक्षा 1 का दायरा बहुत अधिक है:

• कक्षा 1 रेंज: 96 – 65 = 31
• कक्षा 2 की सीमा: 91 – 71 = 20

कक्षा 1 की अंतरचतुर्थक सीमा भी बहुत अधिक है:

• कक्षा 1 अंतरचतुर्थक सीमा: 90.25 – 71 = 19.25
• कक्षा 2 अंतरचतुर्थक सीमा: 84.25 – 74.75 = 9.5

कक्षा 1 का मानक विचलन भी बहुत अधिक है:

• कक्षा 1 मानक विचलन: 10.21
• कक्षा 2 का मानक विचलन: 6.43

इनमें से प्रत्येक उपाय हमें बताता है कि कक्षा 1 के छात्रों के लिए परीक्षा अंकों में अंतर कक्षा 2 के छात्रों की तुलना में बहुत अधिक है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि एक्सेल में अन्य सामान्य ऑपरेशन कैसे करें:

एक्सेल में सारांश तालिका कैसे बनाएं
एक्सेल में समूह द्वारा माध्यिका की गणना कैसे करें
एक्सेल में मानक विचलन की गणना कैसे करें और शून्य को कैसे अनदेखा करें