सतत और श्रेणीबद्ध चर के बीच सहसंबंध की गणना कैसे करें
जब हम दो सतत चरों के बीच सहसंबंध की गणना करना चाहते हैं, तो हम आम तौर पर पियर्सन सहसंबंध गुणांक का उपयोग करते हैं।
हालाँकि, जब हम एक सतत चर और एक श्रेणीगत चर के बीच सहसंबंध की गणना करना चाहते हैं, तो हम बिंदु द्विक्रमिक सहसंबंध का उपयोग कर सकते हैं।
बिंदु द्विक्रमिक सहसंबंध का उपयोग एक द्विआधारी श्रेणीबद्ध चर (एक चर जो केवल दो मान ले सकता है) और एक सतत चर के बीच सहसंबंध की गणना करने के लिए किया जाता है और इसमें निम्नलिखित गुण होते हैं:
- बिंदु-द्विक्रमिक सहसंबंध -1 और 1 के बीच भिन्न हो सकता है।
- बाइनरी वैरिएबल द्वारा बनाए गए प्रत्येक समूह के लिए, यह माना जाता है कि निरंतर वैरिएबल सामान्य रूप से समान भिन्नताओं के साथ वितरित किया जाता है।
- बाइनरी वैरिएबल द्वारा बनाए गए प्रत्येक समूह के लिए, यह माना जाता है कि कोई चरम आउटलेर नहीं हैं।
निम्नलिखित उदाहरण दिखाता है कि व्यवहार में बिंदु-द्विक्रमिक सहसंबंध की गणना कैसे करें।
उदाहरण: बिंदु-द्विक्रमिक सहसंबंध की गणना
मान लीजिए कि एक विश्वविद्यालय प्रोफेसर यह निर्धारित करना चाहता है कि किसी विशेष योग्यता परीक्षा में लिंग और स्कोर के बीच कोई संबंध है या नहीं।
वह अपनी कक्षा में 12 लड़कों और 12 लड़कियों पर निम्नलिखित डेटा एकत्र करता है:
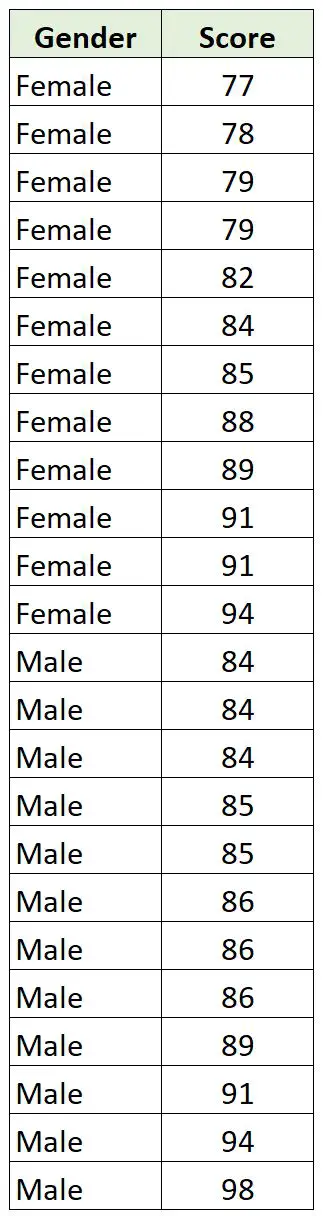
चूँकि लिंग एक श्रेणीबद्ध चर है और स्कोर एक सतत चर है, इसलिए दो चर के बीच एक बिंदु-द्विक्रमिक सहसंबंध की गणना करना समझ में आता है।
प्रोफेसर दो चर के बीच बिंदु-द्विक्रमिक सहसंबंध की गणना करने के लिए किसी भी सांख्यिकीय सॉफ्टवेयर (एक्सेल, आर, पायथन, एसपीएसएस, स्टाटा सहित) का उपयोग कर सकते हैं।
निम्नलिखित कोड दिखाता है कि लिंग चर के लिए महिलाओं का प्रतिनिधित्व करने के लिए मान 0 और पुरुषों का प्रतिनिधित्व करने के लिए 1 का उपयोग करके आर में बिंदु-द्विक्रमिक सहसंबंध की गणना कैसे करें:
#define values for gender gender <- c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1) #define values for score score <- c(77, 78, 79, 79, 82, 84, 85, 88, 89, 91, 91, 94, 84, 84, 84, 85, 85, 86, 86, 86, 89, 91, 94, 98) #calculate point-biserial correlation horn. test (gender, score) Pearson's product-moment correlation data: gender and score t = 1.3739, df = 22, p-value = 0.1833 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: -0.1379386 0.6147832 sample estimates: horn 0.2810996
परिणाम से, हम देख सकते हैं कि बिंदु-द्विक्रमिक सहसंबंध गुणांक 0.281 है और संबंधित पी-मान 0.1833 है।
चूँकि सहसंबंध गुणांक सकारात्मक है, यह हमें बताता है कि लिंग और स्कोर के बीच सकारात्मक सहसंबंध है।
चूँकि हमने पुरुषों को 1 और महिलाओं को 0 के रूप में कोडित किया है, यह इंगित करता है कि पुरुषों के लिए स्कोर अधिक होते हैं (यानी, लिंग “बढ़ने” के साथ स्कोर बढ़ने लगते हैं)। » 0 से 1 तक).
हालाँकि, चूंकि पी-वैल्यू 0.05 से कम नहीं है, इसलिए यह सहसंबंध गुणांक सांख्यिकीय रूप से महत्वपूर्ण नहीं है।
अतिरिक्त संसाधन
निम्नलिखित ट्यूटोरियल बताते हैं कि विभिन्न सांख्यिकीय सॉफ़्टवेयर का उपयोग करके बिंदु द्विक्रमिक सहसंबंध की गणना कैसे करें:
एक्सेल में बिंदु-द्विक्रमिक सहसंबंध की गणना कैसे करें
आर में बिंदु-द्विक्रमिक सहसंबंध की गणना कैसे करें
पायथन में बिंदु-द्विक्रमिक सहसंबंध की गणना कैसे करें