निरपेक्ष आवृत्ति हिस्टोग्राम

यह आलेख बताता है कि निरपेक्ष आवृत्ति हिस्टोग्राम क्या हैं। इसलिए आप जानेंगे कि पूर्ण आवृत्ति हिस्टोग्राम कैसे बनाया जाता है और साथ ही इस प्रकार के सांख्यिकीय आरेख के उदाहरण भी।

निरपेक्ष आवृत्ति हिस्टोग्राम क्या है?

निरपेक्ष आवृत्ति हिस्टोग्राम एक प्रकार का हिस्टोग्राम है जिसमें डेटा सेट की निरपेक्ष आवृत्तियों का प्रतिनिधित्व किया जाता है।

निरपेक्ष आवृत्ति हिस्टोग्राम निश्चित रूप से आंकड़ों में हिस्टोग्राम का सबसे अधिक उपयोग किया जाने वाला प्रकार है।

पूर्ण आवृत्ति हिस्टोग्राम में प्रत्येक बार की चौड़ाई अंतराल की चौड़ाई के समानुपाती होती है और ऊँचाई अंतराल की पूर्ण आवृत्ति के समानुपाती होती है।

निरपेक्ष आवृत्ति हिस्टोग्राम कैसे बनाएं

पूर्ण आवृत्ति हिस्टोग्राम बनाने के लिए, आपको इन चरणों का पालन करना होगा:

1. डेटा श्रृंखला के आधार पर हिस्टोग्राम के क्षैतिज अक्ष को अंतरालों में विभाजित करें।
2. हिस्टोग्राम के ऊर्ध्वाधर अक्ष पर अंतरालों की पूर्ण आवृत्ति मानों का प्रतिनिधित्व करें।
3. प्रत्येक अंतराल के लिए, अंतराल की पूर्ण आवृत्ति के बराबर ऊंचाई वाली एक आयताकार पट्टी बनाएं। ध्यान दें कि लगातार दो अंतरालों की छड़ें स्पर्श करनी चाहिए।

निरपेक्ष आवृत्ति हिस्टोग्राम उदाहरण

एक बार जब हमने पूर्ण आवृत्ति हिस्टोग्राम की परिभाषा देख ली है और यह कैसे किया जाता है, तो आप अवधारणा को बेहतर ढंग से समझने के लिए नीचे इस प्रकार का हिस्टोग्राम देख सकते हैं।

• सांख्यिकीय डेटा के निम्नलिखित सेट को पूर्ण आवृत्ति हिस्टोग्राम में प्लॉट करें:

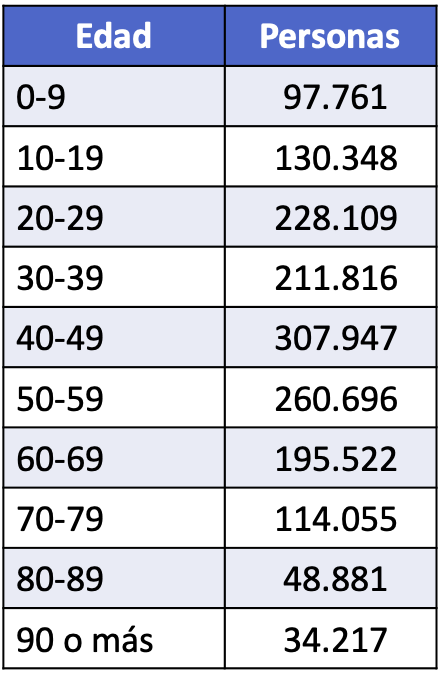
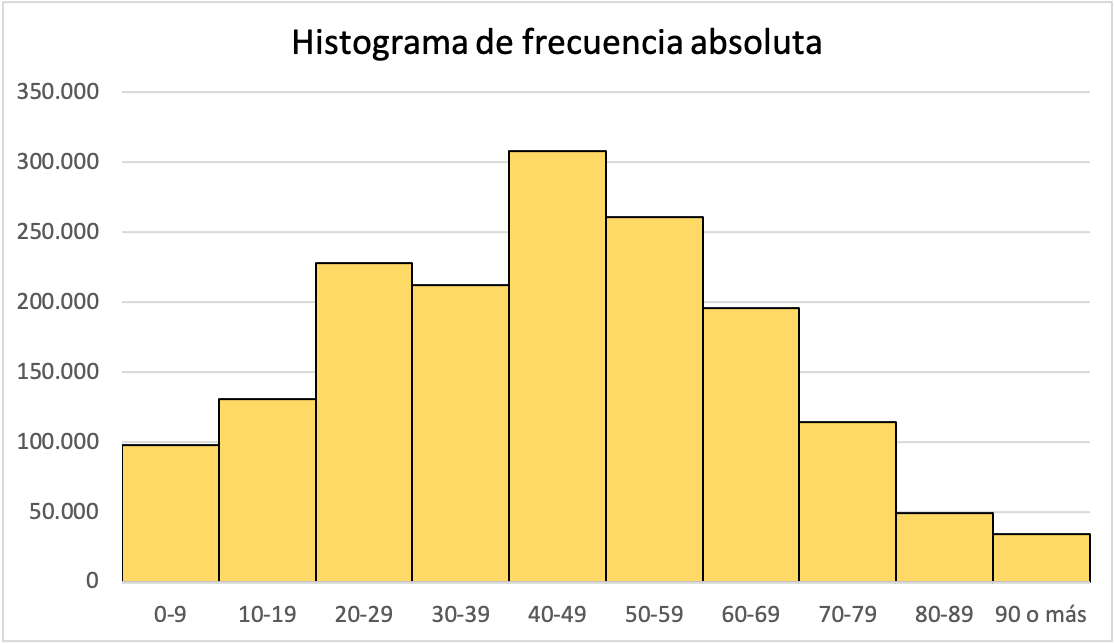
हिस्टोग्राम बनाने के लिए हमें ऊपर बताए गए चरणों का पालन करना होगा। अर्थात्, हम पहले क्षैतिज अक्ष पर आयु अंतराल का प्रतिनिधित्व करते हैं, फिर हम ऊर्ध्वाधर अक्ष को मापते हैं और अंत में, हम प्रत्येक अंतराल को उसकी पूर्ण आवृत्ति के बराबर ऊंचाई स्तंभ के माध्यम से दर्शाते हैं।

संचयी निरपेक्ष आवृत्ति हिस्टोग्राम

संचयी निरपेक्ष आवृत्ति हिस्टोग्राम में हिस्टोग्राम में प्रत्येक अंतराल की संचयी निरपेक्ष आवृत्तियों का प्रतिनिधित्व होता है।

याद रखें कि किसी अंतराल की संचयी निरपेक्ष आवृत्ति पिछले सभी अंतरालों की सभी निरपेक्ष आवृत्तियों और अंतराल की पूर्ण आवृत्ति का योग है।

उदाहरण के तौर पर, हम निम्नलिखित आवृत्ति तालिका के साथ इस प्रकार के हिस्टोग्राम का प्रतिनिधित्व करेंगे:

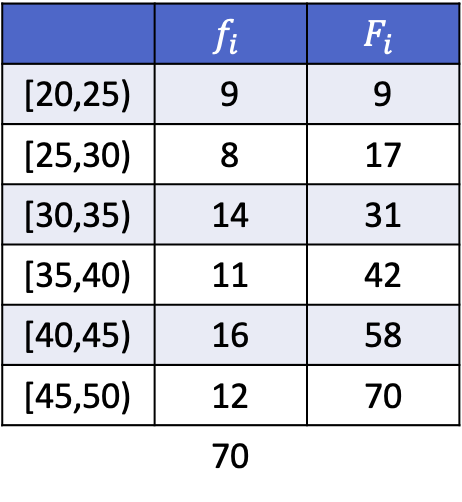
कॉलम _फाई अंतराल की पूर्ण आवृत्ति से मेल खाता है और कॉलम एफ _आई प्रत्येक अंतराल की संचयी निरपेक्ष आवृत्ति है, क्योंकि यह उक्त अंतराल तक सभी पूर्ण आवृत्तियों का योग है। इसलिए, हमें कॉलम F _i में डेटा के साथ एक हिस्टोग्राम बनाने की आवश्यकता है।

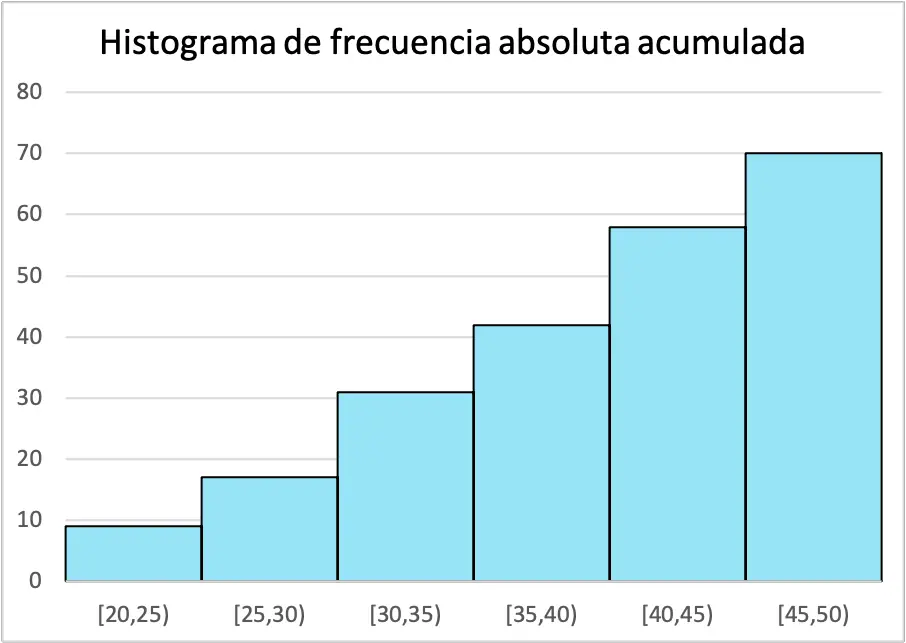
ध्यान दें कि स्तंभों की ऊंचाई जमा हो जाती है, क्योंकि हिस्टोग्राम संचित निरपेक्ष आवृत्तियों का प्रतिनिधित्व करता है।

निरपेक्ष आवृत्ति हिस्टोग्राम और सापेक्ष आवृत्ति हिस्टोग्राम

सांख्यिकी में व्यापक रूप से उपयोग किया जाने वाला एक अन्य प्रकार का हिस्टोग्राम सापेक्ष आवृत्ति हिस्टोग्राम है। तो इस अनुभाग में हम देखेंगे कि इस प्रकार के सांख्यिकीय ग्राफ़ कैसे भिन्न होते हैं।

निरपेक्ष आवृत्ति हिस्टोग्राम और सापेक्ष आवृत्ति हिस्टोग्राम के बीच का अंतर उनके द्वारा दर्शाए जाने वाले डेटा के प्रकार का है। एक पूर्ण आवृत्ति हिस्टोग्राम डेटा सेट की पूर्ण आवृत्तियों से बनाया जाता है, जबकि एक सापेक्ष आवृत्ति हिस्टोग्राम डेटा सेट की सापेक्ष आवृत्तियों का प्रतिनिधित्व करता है।

यह ध्यान दिया जाना चाहिए कि निरपेक्ष आवृत्ति और सापेक्ष आवृत्ति हिस्टोग्राम के स्तंभों का आकार बिल्कुल समान होता है, निरपेक्ष मानों को केवल सापेक्ष मानों द्वारा प्रतिस्थापित किया जाता है।