पायथन में कर्व फिटिंग (उदाहरण के साथ)

अक्सर आप पायथन में डेटासेट में एक कर्व फिट करना चाह सकते हैं।

निम्नलिखित चरण-दर-चरण उदाहरण बताता है कि numpy.polyfit() फ़ंक्शन का उपयोग करके पायथन में डेटा में कर्व्स को कैसे फिट किया जाए और यह कैसे निर्धारित किया जाए कि कौन सा कर्व डेटा के लिए सबसे उपयुक्त है।

चरण 1: डेटा बनाएं और विज़ुअलाइज़ करें

आइए एक नकली डेटासेट बनाकर शुरुआत करें, फिर डेटा की कल्पना करने के लिए एक स्कैटरप्लॉट बनाएं:

 import pandas as pd
import matplotlib. pyplot as plt

#createDataFrame
df = pd. DataFrame ({' x ': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15],
                   ' y ': [3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46]})

#create scatterplot of x vs. y
plt. scatter (df. x , df. y ) 

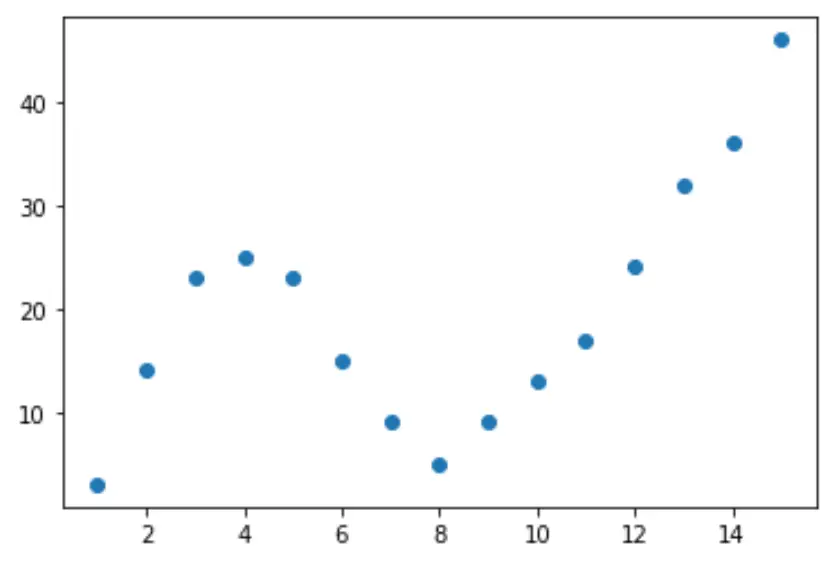
चरण 2: एकाधिक वक्र समायोजित करें

आइए फिर डेटा में कई बहुपद प्रतिगमन मॉडल फिट करें और एक ही प्लॉट में प्रत्येक मॉडल के वक्र की कल्पना करें:

 import numpy as np

#fit polynomial models up to degree 5
model1 = np. poly1d (np. polyfit (df. x , df. y , 1))
model2 = np. poly1d (np. polyfit (df. x , df. y , 2))
model3 = np. poly1d (np. polyfit (df. x , df. y , 3))
model4 = np. poly1d (np. polyfit (df. x , df. y , 4))
model5 = np. poly1d (np. polyfit (df. x , df. y , 5))

#create scatterplot
polyline = np. linspace (1, 15, 50)
plt. scatter (df. x , df. y )

#add fitted polynomial lines to scatterplot 
plt. plot (polyline, model1(polyline), color=' green ')
plt. plot (polyline, model2(polyline), color=' red ')
plt. plot (polyline, model3(polyline), color=' purple ')
plt. plot (polyline, model4(polyline), color=' blue ')
plt. plot (polyline, model5(polyline), color=' orange ')
plt. show ()

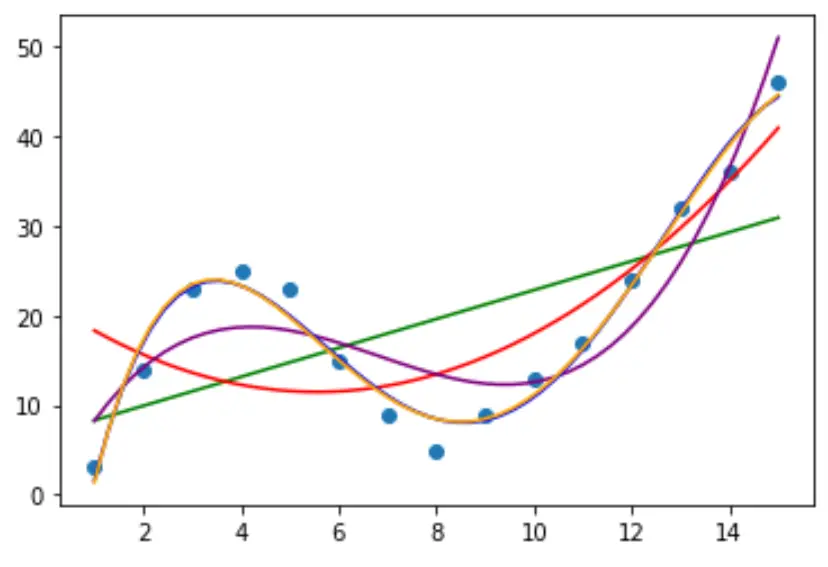
यह निर्धारित करने के लिए कि कौन सा वक्र डेटा के लिए सबसे उपयुक्त है, हम प्रत्येक मॉडल के समायोजित आर वर्ग को देख सकते हैं।

यह मान हमें प्रतिक्रिया चर में भिन्नता का प्रतिशत बताता है जिसे मॉडल में भविष्यवक्ता चर द्वारा समझाया जा सकता है, जिसे भविष्यवक्ता चर की संख्या के लिए समायोजित किया जाता है।

 #define function to calculate adjusted r-squared
def adjR(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar)**2)
    sstot = np. sum ((y - ybar)**2)
    results[' r_squared '] = 1- (((1-(ssreg/sstot))*(len(y)-1))/(len(y)-degree-1))

    return results

#calculated adjusted R-squared of each model
adjR(df. x , df. y , 1)
adjR(df. x , df. y , 2)
adjR(df. x , df. y , 3)
adjR(df. x , df. y , 4)
adjR(df. x , df. y , 5)

{'r_squared': 0.3144819}
{'r_squared': 0.5186706}
{'r_squared': 0.7842864}
{'r_squared': 0.9590276}
{'r_squared': 0.9549709}

परिणाम से, हम देख सकते हैं कि उच्चतम समायोजित आर-वर्ग वाला मॉडल चौथी डिग्री बहुपद है, जिसका समायोजित आर-वर्ग 0.959 है।

चरण 3: अंतिम वक्र की कल्पना करें

अंत में, हम चौथी डिग्री बहुपद मॉडल के वक्र के साथ एक स्कैटर प्लॉट बना सकते हैं:

 #fit fourth-degree polynomial
model4 = np. poly1d (np. polyfit (df. x , df. y , 4))

#define scatterplot
polyline = np. linspace (1, 15, 50)
plt. scatter (df. x , df. y )

#add fitted polynomial curve to scatterplot
plt. plot (polyline, model4(polyline), ' -- ', color=' red ')
plt. show ()

हम print() फ़ंक्शन का उपयोग करके इस पंक्ति के लिए समीकरण भी प्राप्त कर सकते हैं:

 print (model4)

          4 3 2
-0.01924x + 0.7081x - 8.365x + 35.82x - 26.52

वक्र का समीकरण इस प्रकार है:

y = -0.01924x ⁴ + 0.7081x ³ – 8.365x ² + 35.82x – 26.52

हम मॉडल में भविष्यवक्ता चर के आधार पर प्रतिक्रिया चर के मूल्य की भविष्यवाणी करने के लिए इस समीकरण का उपयोग कर सकते हैं। उदाहरण के लिए यदि x = 4 है तो हम अनुमान लगाएंगे कि y = 23.32 :

y = -0.0192(4) ⁴ + 0.7081(4) ³ – 8.365(4) ² + 35.82(4) – 26.52 = 23.32

अतिरिक्त संसाधन

बहुपद प्रतिगमन का एक परिचय
पायथन में बहुपद प्रतिगमन कैसे करें