पायथन में सामान्यता का परीक्षण कैसे करें (4 तरीके)

कई सांख्यिकीय परीक्षण मानते हैं कि डेटा सेट सामान्य रूप से वितरित होते हैं।

पायथन में इस परिकल्पना की जाँच करने के चार सामान्य तरीके हैं:

1. (दृश्य विधि) एक हिस्टोग्राम बनाएं।

• यदि हिस्टोग्राम लगभग “घंटी” के आकार का है, तो डेटा को सामान्य रूप से वितरित माना जाता है।

2. (दृश्य विधि) एक QQ प्लॉट बनाएं।

• यदि प्लॉट पर बिंदु मोटे तौर पर एक सीधी विकर्ण रेखा के साथ स्थित हैं, तो डेटा को सामान्य रूप से वितरित माना जाता है।

3. (औपचारिक सांख्यिकीय परीक्षण) शापिरो-विल्क परीक्षण करें।

• यदि परीक्षण का पी-मान α = 0.05 से अधिक है, तो डेटा को सामान्य रूप से वितरित माना जाता है।

4. (औपचारिक सांख्यिकीय परीक्षण) कोलमोगोरोव-स्मिरनोव परीक्षण करें।

• यदि परीक्षण का पी-मान α = 0.05 से अधिक है, तो डेटा को सामान्य रूप से वितरित माना जाता है।

निम्नलिखित उदाहरण दिखाते हैं कि व्यवहार में इनमें से प्रत्येक विधि का उपयोग कैसे करें।

विधि 1: एक हिस्टोग्राम बनाएँ

निम्नलिखित कोड दिखाता है कि लॉग-सामान्य वितरण का अनुसरण करने वाले डेटा सेट के लिए हिस्टोग्राम कैसे बनाया जाए:

 import math
import numpy as np
from scipy. stats import lognorm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create histogram to visualize values in dataset
plt. hist (lognorm_dataset, edgecolor=' black ', bins=20) 

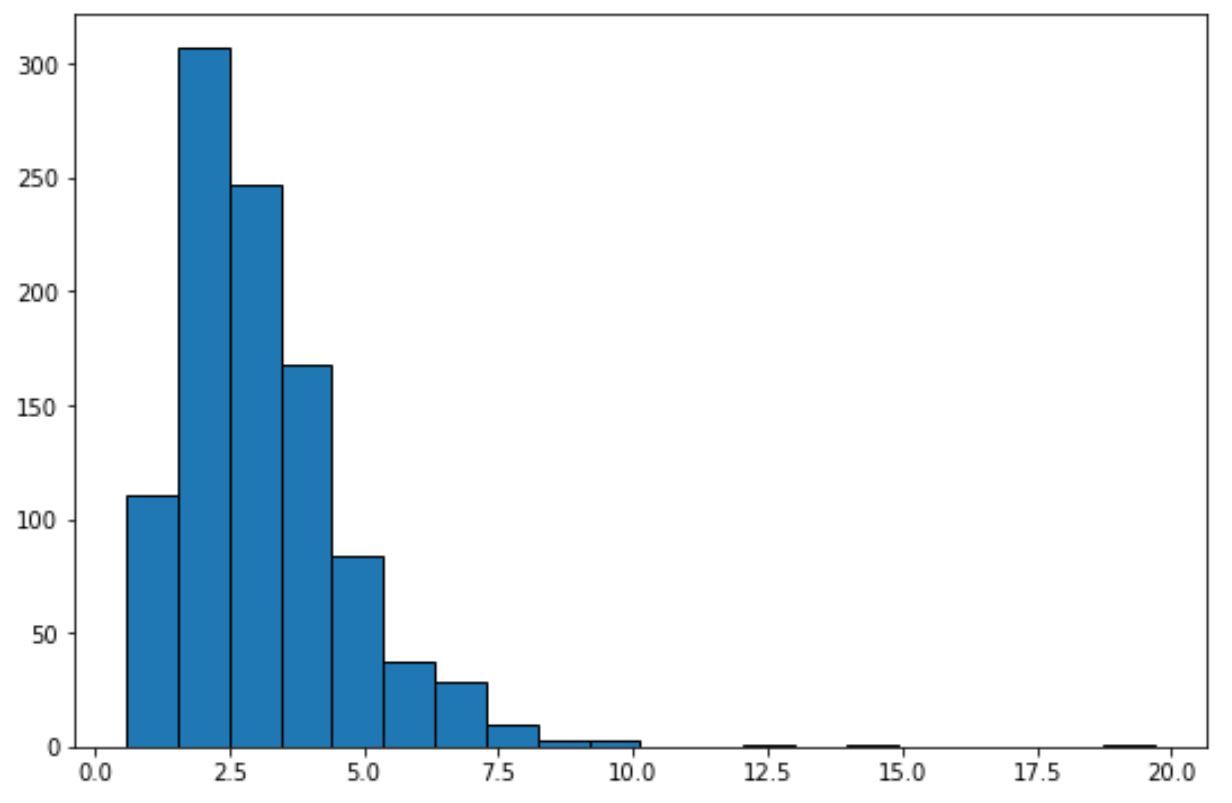
केवल इस हिस्टोग्राम को देखकर, हम बता सकते हैं कि डेटासेट “घंटी के आकार” को प्रदर्शित नहीं करता है और सामान्य रूप से वितरित नहीं किया जाता है।

विधि 2: एक QQ प्लॉट बनाएं

निम्नलिखित कोड दिखाता है कि लॉग-सामान्य वितरण का पालन करने वाले डेटा सेट के लिए QQ प्लॉट कैसे बनाया जाए:

 import math
import numpy as np
from scipy. stats import lognorm
import statsmodels. api as sm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create QQ plot with 45-degree line added to plot
fig = sm. qqplot (lognorm_dataset, line=' 45 ')

plt. show ()

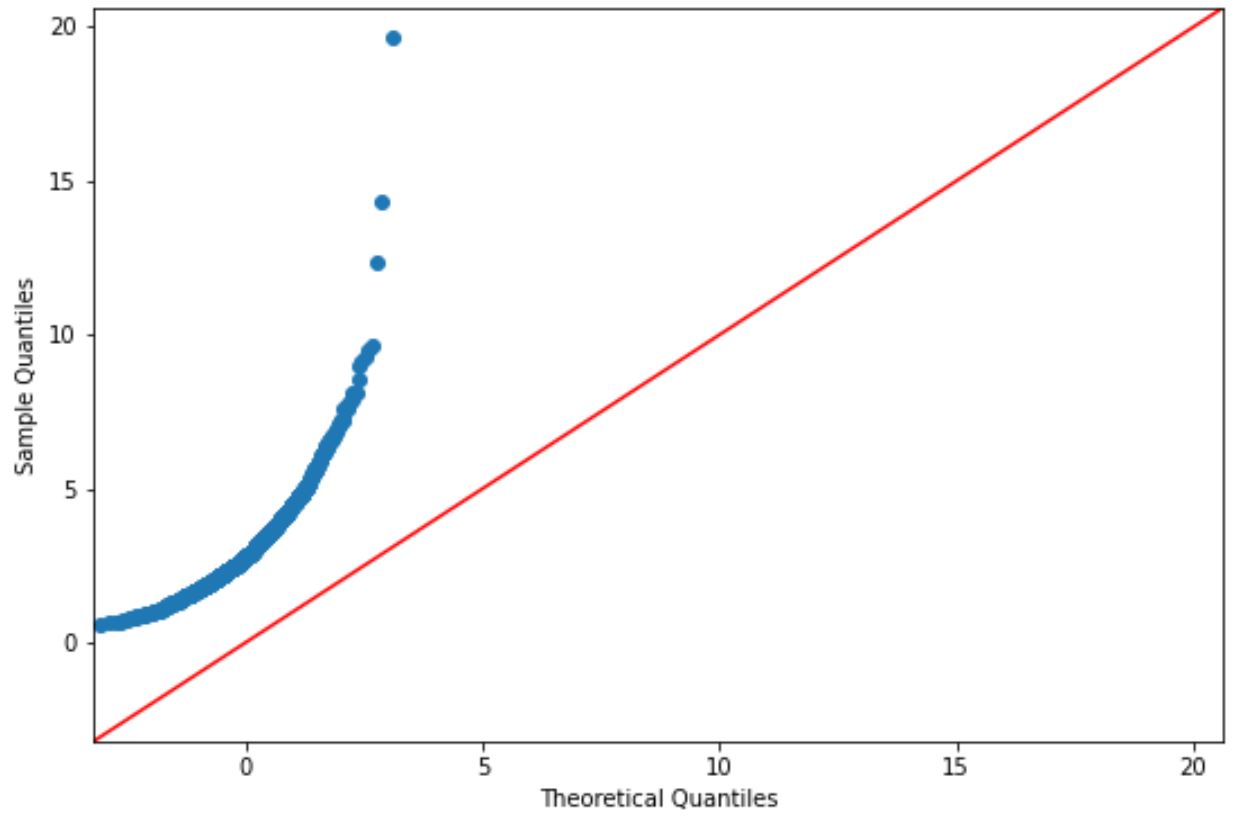
यदि प्लॉट बिंदु लगभग एक सीधी विकर्ण रेखा के साथ स्थित हैं, तो हम आम तौर पर मानते हैं कि डेटा सेट सामान्य रूप से वितरित किया जाता है।

हालाँकि, इस ग्राफ़ के बिंदु स्पष्ट रूप से लाल रेखा के अनुरूप नहीं हैं, इसलिए हम यह नहीं मान सकते कि यह डेटा सेट सामान्य रूप से वितरित है।

यह समझ में आना चाहिए कि हमने लॉग-सामान्य वितरण फ़ंक्शन का उपयोग करके डेटा तैयार किया है।

विधि 3: शापिरो-विल्क परीक्षण करें

निम्नलिखित कोड दिखाता है कि लॉग-सामान्य वितरण का पालन करने वाले डेटा सेट के लिए शापिरो-विल्क कैसे निष्पादित करें:

 import math
import numpy as np
from scipy.stats import shapiro 
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Shapiro-Wilk test for normality
shapiro(lognorm_dataset)

ShapiroResult(statistic=0.8573324680328369, pvalue=3.880663073872444e-29)

परिणाम से, हम देख सकते हैं कि परीक्षण आँकड़ा 0.857 है और संबंधित पी-मान 3.88e-29 (शून्य के बेहद करीब) है।

चूँकि पी-मान 0.05 से कम है, हम शापिरो-विल्क परीक्षण की शून्य परिकल्पना को अस्वीकार करते हैं।

इसका मतलब यह है कि हमारे पास यह कहने के लिए पर्याप्त सबूत हैं कि नमूना डेटा सामान्य वितरण से नहीं आता है।

विधि 4: कोलमोगोरोव-स्मिरनोव परीक्षण करें

निम्नलिखित कोड दिखाता है कि लॉग-सामान्य वितरण का पालन करने वाले डेटा सेट के लिए कोलमोगोरोव-स्मिरनोव परीक्षण कैसे करें:

 import math
import numpy as np
from scipy.stats import kstest
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Kolmogorov-Smirnov test for normality
kstest(lognorm_dataset, ' norm ')

KstestResult(statistic=0.84125708308077, pvalue=0.0)

परिणाम से, हम देख सकते हैं कि परीक्षण आँकड़ा 0.841 है और संबंधित पी-मान 0.0 है।

चूँकि पी-मान 0.05 से कम है, हम कोलमोगोरोव-स्मिरनोव परीक्षण की शून्य परिकल्पना को अस्वीकार करते हैं।

इसका मतलब यह है कि हमारे पास यह कहने के लिए पर्याप्त सबूत हैं कि नमूना डेटा सामान्य वितरण से नहीं आता है।

गैर-सामान्य डेटा को कैसे प्रबंधित करें

यदि किसी दिए गए डेटा सेट को सामान्य रूप से वितरित नहीं किया जाता है , तो हम इसे अधिक सामान्य रूप से वितरित करने के लिए अक्सर निम्नलिखित परिवर्तनों में से एक कर सकते हैं:

1. लॉग परिवर्तन: x मानों को log(x) में बदलें।

2. वर्गमूल परिवर्तन: x के मानों को √x में बदलें।

3. घनमूल परिवर्तन: x के मानों को x ^1/3 में परिवर्तित करें।

इन परिवर्तनों को निष्पादित करने से, डेटासेट आम तौर पर अधिक सामान्य रूप से वितरित हो जाता है।

पायथन में इन परिवर्तनों को कैसे करें यह देखने के लिए इस ट्यूटोरियल को पढ़ें।