पियर्सन सहसंबंध गुणांक

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 5, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि पियर्सन सहसंबंध गुणांक (या रैखिक सहसंबंध गुणांक) क्या है और इसका उपयोग किस लिए किया जाता है। आप चरण-दर-चरण अभ्यास के साथ सीखेंगे कि पियर्सन सहसंबंध गुणांक की गणना कैसे करें। इसके अतिरिक्त, आप अंत में ऑनलाइन कैलकुलेटर के साथ किसी भी डेटासेट का पियर्सन सहसंबंध गुणांक मान पा सकते हैं।

पियर्सन का सहसंबंध गुणांक क्या है?

पियर्सन सहसंबंध गुणांक , जिसे रैखिक सहसंबंध गुणांक या केवल सहसंबंध गुणांक भी कहा जाता है, एक सांख्यिकीय माप है जो दो चर के बीच संबंध को इंगित करता है।

दो चरों के बीच पियर्सन सहसंबंध गुणांक की गणना करने के लिए, आपको उक्त चरों के सहप्रसरण को उनके प्रसरणों के उत्पाद के वर्गमूल से विभाजित करना होगा।

इस प्रकार, पियर्सन सहसंबंध गुणांक दो मात्रात्मक यादृच्छिक चर के बीच रैखिक निर्भरता को मापने का प्रयास करता है। एक प्राथमिकता, संख्यात्मक रूप से चर के बीच सहसंबंध का मूल्यांकन करना जटिल है क्योंकि यह निर्धारित करना मुश्किल है कि चर की जोड़ी के बीच अधिक सहसंबद्ध है, जैसे कि प्यूस में, पियर्सन के सहसंबंध गुणांक का उद्देश्य चर के बीच के संबंध को महत्व देना है ताकि सक्षम किया जा सके। उनके बीच तुलना करें.

पियर्सन सहसंबंध सूचकांक का मान -1 और +1 के बीच है। हम नीचे देखेंगे कि पियर्सन सहसंबंध गुणांक के मूल्य की व्याख्या कैसे की जाती है।

पियर्सन सहसंबंध गुणांक सूत्र

दो सांख्यिकीय चरों का पियर्सन सहसंबंध गुणांक चरों के सहप्रसरण और प्रत्येक चर के प्रसरण के उत्पाद के वर्गमूल के बीच के भागफल के बराबर है।

इसलिए, पियर्सन सहसंबंध गुणांक की गणना का सूत्र इस प्रकार है:

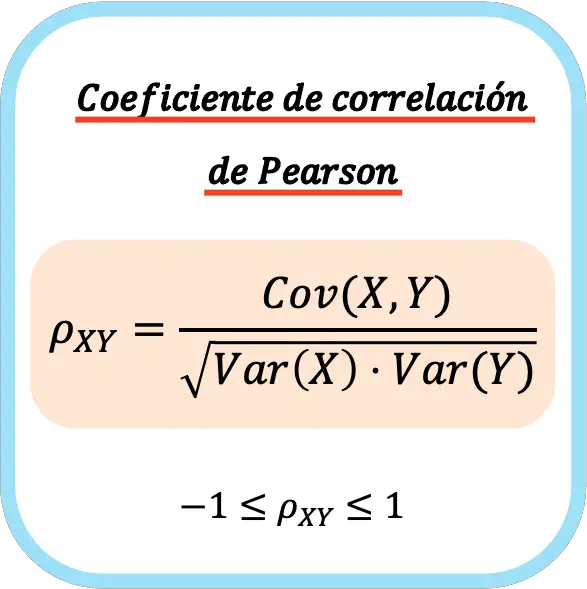
पियर्सन सहसंबंध गुणांक, रैखिक सहसंबंध गुणांक

👉 आप किसी भी डेटा सेट के लिए पियर्सन सहसंबंध गुणांक की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।

जब किसी जनसंख्या पर पियर्सन सहसंबंध गुणांक की गणना की जाती है, तो इसे आम तौर पर ग्रीक अक्षर ρ द्वारा व्यक्त किया जाता है। लेकिन जब किसी नमूने के सापेक्ष गुणांक की गणना की जाती है, तो अक्षर r आमतौर पर एक प्रतीक के रूप में उपयोग किया जाता है।

ध्यान रखें कि पियर्सन सहसंबंध गुणांक निर्धारित करने के लिए, यह आवश्यक है कि आप दो चरों के बीच सहप्रसरण और एक चर के प्रसरण की गणना करना जानते हों। इसके अतिरिक्त, आपको यह समझने की आवश्यकता है कि इन सांख्यिकीय उपायों का क्या मतलब है। इसलिए, स्पष्टीकरण जारी रखने से पहले, निम्नलिखित दो लेख पढ़ने की अनुशंसा की जाती है:

➤ देखें: सहप्रसरण की गणना कैसे करें
➤ देखें: गैप की गणना कैसे करें

पियर्सन सहसंबंध गुणांक की गणना का उदाहरण

पियर्सन के सहसंबंध गुणांक की परिभाषा और उसके सूत्र को ध्यान में रखते हुए, नीचे एक चरण-दर-चरण उदाहरण दिया गया है ताकि आप देख सकें कि इसकी गणना कैसे की जाती है।

निम्नलिखित दो सतत चरों के बीच पियर्सन सहसंबंध गुणांक की गणना करें:

पियर्सन सहसंबंध गुणांक की गणना करने से पहले, हम दो चर के बीच संबंध का विश्लेषण करने के लिए एक स्कैटरप्लॉट में डेटासेट का प्रतिनिधित्व करेंगे:

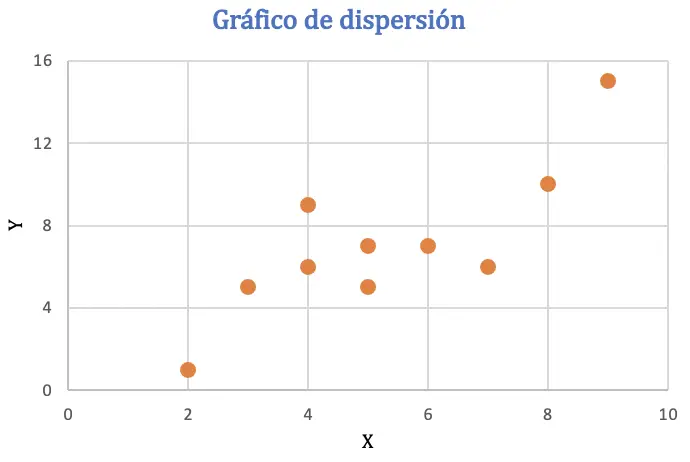
स्कैटर प्लॉट से, यह अनुमान लगाया जा सकता है कि डेटा में सकारात्मक प्रवृत्ति हो सकती है, या दूसरे शब्दों में, जब एक चर का मूल्य बढ़ता है, तो दूसरा चर भी बढ़ता है। सहसंबंध की जांच करने के लिए, हम पियर्सन गुणांक पाएंगे।

करने वाली पहली चीज़ प्रत्येक चर का अलग-अलग अंकगणितीय माध्य ज्ञात करना है, जो अवलोकनों की संख्या से विभाजित डेटा के कुल योग के बराबर है।

$\overline{x}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}=\cfrac{53}{10}=5,3$

$\overline{y}=\cfrac{\displaystyle \sum_{i=1}^n y_i}{n}=\cfrac{71}{10}=7,1$

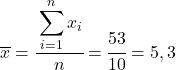
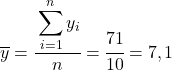
अब जब हम प्रत्येक चर का माध्य जानते हैं, तो हमें डेटा तालिका में निम्नलिखित कॉलम जोड़ने होंगे:

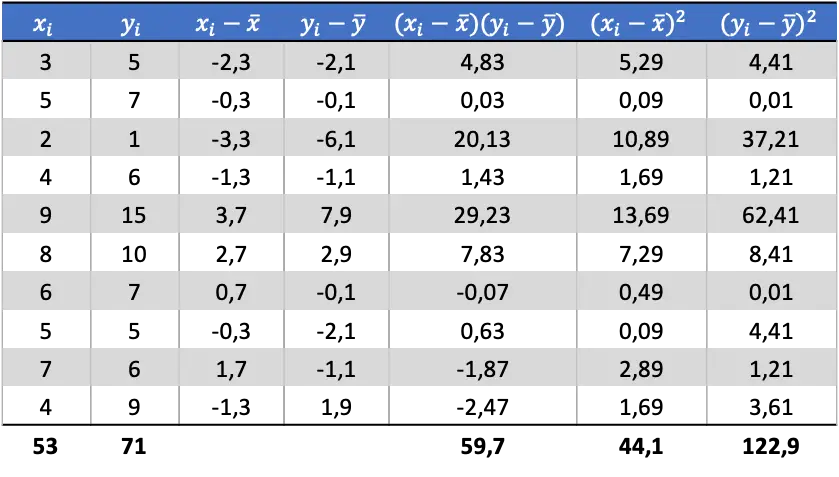
तालिका में गणना किए गए डेटा से, हम सहप्रसरण और प्रसरण के मान निर्धारित करते हैं (यदि आपको याद नहीं है कि यह कैसे किया गया था, तो ऊपर दो लिंक हैं जहां इसे विस्तार से समझाया गया है):

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}=\cfrac{59,7}{10}=5,97$

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}=\cfrac{44,1}{10}=4,41$

$Var(Y)=\cfrac{\displaystyle\sum_{i=1}^n\left(y_i-\overline{y}\right)^2}{n}=\cfrac{122,9}{10}=12,29$

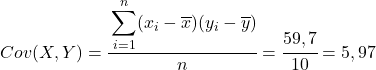
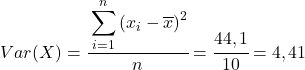
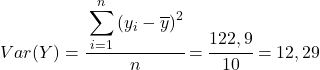
अंत में, इसका मान प्राप्त करने के लिए बस पियर्सन सहसंबंध गुणांक सूत्र लागू करें:

$\rho_{XY}=\cfrac{Cov(X,Y)}{\sqrt{Var(X)\cdot Var(Y)}}=\cfrac{5,97}{\sqrt{4,41\cdot 12,29}}=0,81$

पियर्सन सहसंबंध गुणांक का मान 1 के बहुत करीब है, जिसका अर्थ है कि इन दो चरों में काफी मजबूत सकारात्मक सहसंबंध है।

जैसा कि आपने देखा है, पियर्सन सहसंबंध गुणांक निर्धारित करने के लिए कॉलम गणनाओं को अधिक तेज़ी से करने के लिए एक्सेल जैसे प्रोग्राम का उपयोग करना बहुत उपयोगी है।

पियर्सन सहसंबंध गुणांक कैलकुलेटर

दो चरों के बीच पियर्सन सहसंबंध गुणांक की गणना करने के लिए निम्नलिखित कैलकुलेटर में सांख्यिकीय डेटा का एक सेट दर्ज करें। आपको डेटा जोड़े को अलग करने की आवश्यकता है, ताकि पहले बॉक्स में केवल एक वेरिएबल के मान हों और दूसरे बॉक्स में केवल दूसरे वेरिएबल के मान हों।

डेटा को एक स्थान से अलग किया जाना चाहिए और दशमलव विभाजक के रूप में अवधि का उपयोग करके दर्ज किया जाना चाहिए।

पियर्सन सहसंबंध गुणांक की व्याख्या करना

इस अनुभाग में हम देखेंगे कि पियर्सन सहसंबंध गुणांक की व्याख्या कैसे करें, क्योंकि इसका मूल्य जानना पर्याप्त नहीं है, लेकिन आपको यह जानना होगा कि इसके अर्थ का विश्लेषण कैसे किया जाए।

इस प्रकार पियर्सन सहसंबंध गुणांक की व्याख्या इसके मूल्य पर निर्भर करती है:

r=-1 : दो चरों का पूर्ण नकारात्मक सहसंबंध है, इसलिए हम एक नकारात्मक ढलान वाली एक रेखा खींच सकते हैं जिसमें सभी बिंदु जुड़ते हैं।
-1<r<0 : दो चरों के बीच सहसंबंध नकारात्मक है, इसलिए जब एक चर बढ़ता है तो दूसरा घटता है। मान -1 के जितना करीब होगा, चर उतने ही अधिक नकारात्मक रूप से संबंधित होंगे।
r=0 : दो चरों के बीच सहसंबंध बहुत कमजोर है, वास्तव में, उनके बीच रैखिक संबंध शून्य है। इसका मतलब यह नहीं है कि चर स्वतंत्र हैं, क्योंकि उनका गैर-रैखिक संबंध हो सकता है।
0<r<1 : दो चरों के बीच सहसंबंध सकारात्मक है, मान +1 के जितना करीब होगा, चरों के बीच संबंध उतना ही मजबूत होगा। इस मामले में, जब एक चर का मूल्य बढ़ता है तो दूसरे का भी मूल्य बढ़ता है।
r=1 : दो चरों का पूर्ण सकारात्मक सहसंबंध है, अर्थात उनका सकारात्मक रैखिक संबंध है।

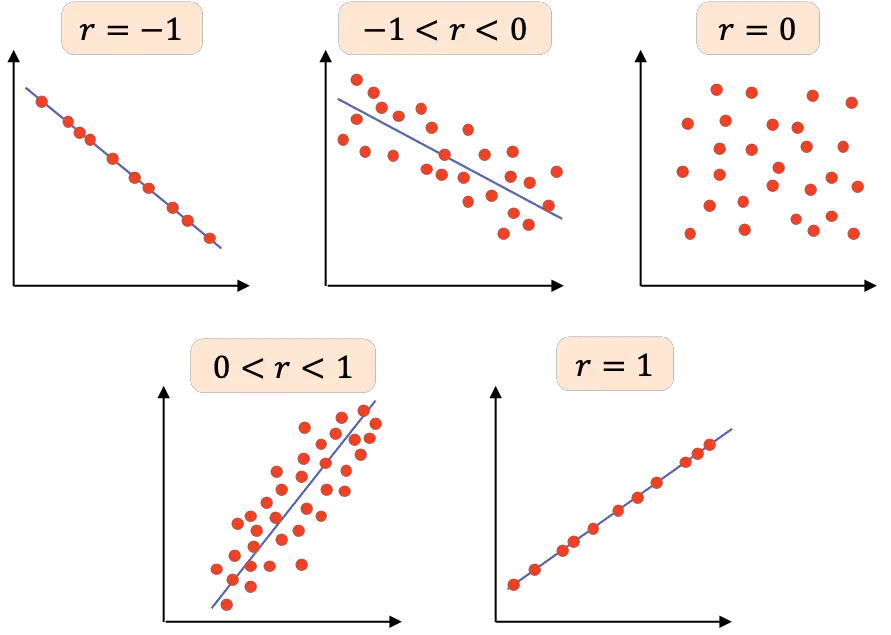
संक्षेप में, निम्नलिखित तालिका पियर्सन सहसंबंध गुणांक की विभिन्न व्याख्याओं के साथ प्रस्तुत की गई है:

कीमत	व्याख्या
आर=-1	पूर्ण नकारात्मक सहसंबंध.
-1<r<0	नकारात्मक सहसंबंध: सहसंबंध -1 के जितना करीब होगा, उतना ही मजबूत होगा।
आर=0	शून्य रैखिक सहसंबंध.
0<आर<1	सकारात्मक सहसंबंध: सहसंबंध +1 के जितना करीब होगा, उतना ही मजबूत होगा।
आर=1	पूर्ण सकारात्मक सहसंबंध.

ध्यान रखें कि यदि दो चरों के बीच कोई संबंध है, तो भी इसका मतलब यह नहीं है कि उनके बीच कार्य-कारण है, अर्थात दो चरों के बीच संबंध का मतलब यह नहीं है कि किसी चर में परिवर्तन ही चर के परिवर्तन का कारण है। अन्य चर.

उदाहरण के लिए, यदि हम पाते हैं कि शरीर में दो अलग-अलग हार्मोनों के उत्पादन के बीच सकारात्मक संबंध है, तो यह आवश्यक नहीं है कि एक हार्मोन में वृद्धि से दूसरे हार्मोन में वृद्धि हो। ऐसा हो सकता है कि शरीर दोनों हार्मोन का उत्पादन करता है क्योंकि उसे किसी बीमारी से लड़ने के लिए दोनों की आवश्यकता होती है और इसलिए दोनों का स्तर एक साथ बढ़ जाता है, ऐसी स्थिति में इसका कारण बीमारी होगी। यह निर्धारित करने के लिए कि क्या दोनों हार्मोनों के बीच कोई कारणात्मक संबंध है, आगे का अध्ययन किया जाना चाहिए।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने