प्रतिगमन ढलान के महत्व का परीक्षण कैसे करें

मान लीजिए कि हमारे पास निम्नलिखित डेटा सेट है जो 12 अलग-अलग घरों का वर्ग फुटेज और कीमत दिखाता है:

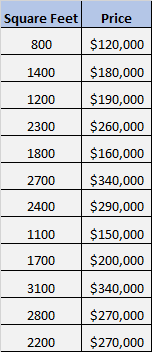
हम जानना चाहते हैं कि क्या वर्गफुटेज और कीमत के बीच कोई महत्वपूर्ण संबंध है।

डेटा कैसा दिखता है इसका अंदाजा लगाने के लिए, हम पहले x-अक्ष पर वर्ग फुट और y-अक्ष पर कीमत के साथ एक स्कैटरप्लॉट बनाते हैं:

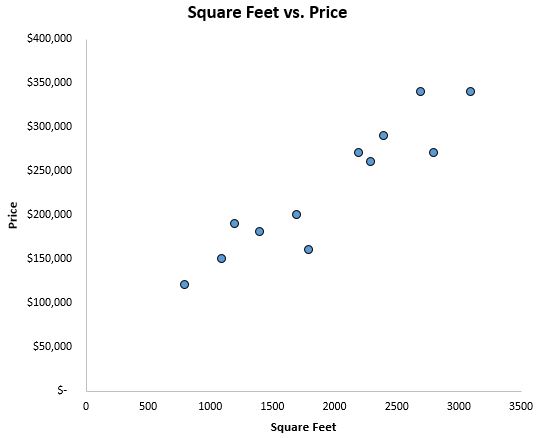
हम स्पष्ट रूप से देख सकते हैं कि वर्गफुटेज और कीमत के बीच एक सकारात्मक संबंध है। जैसे-जैसे वर्ग फ़ुटेज बढ़ता है, घर की कीमत भी बढ़ने लगती है।

हालाँकि, यह पता लगाने के लिए कि क्या वर्ग फुटेज और कीमत के बीच कोई सांख्यिकीय रूप से महत्वपूर्ण संबंध है, हमें एक सरल रैखिक प्रतिगमन चलाने की आवश्यकता है।

इसलिए हम भविष्यवक्ता के रूप में वर्ग फुट और प्रतिक्रिया के रूप में कीमत का उपयोग करके एक सरल रैखिक प्रतिगमन चलाते हैं और निम्नलिखित परिणाम प्राप्त करते हैं:

चाहे आप एक्सेल, एसपीएसएस, आर, या किसी अन्य सॉफ़्टवेयर में एक सरल रैखिक प्रतिगमन चलाएं, आपको ऊपर दिखाए गए परिणाम के समान परिणाम मिलेगा।

याद रखें कि एक साधारण रेखीय प्रतिगमन सर्वोत्तम फिट की रेखा का उत्पादन करेगा, जो उस रेखा का समीकरण है जो हमारे स्कैटरप्लॉट में डेटा को सबसे अच्छी तरह से “फिट” करता है। सर्वोत्तम फ़िट की इस पंक्ति को इस प्रकार परिभाषित किया गया है:

ŷ = बी ₀ + बी ₁ एक्स

जहां ŷ प्रतिक्रिया चर का अनुमानित मूल्य है, बी ₀ अवरोधन है, बी ₁ प्रतिगमन गुणांक है, और एक्स भविष्यवक्ता चर का मूल्य है।

b ₀ का मान मूल के गुणांक द्वारा दिया जाता है, जो 47588.70 है।

बी ₁ का मान भविष्यवक्ता चर स्क्वायर फीट के गुणांक द्वारा दिया गया है, जो 93.57 है।

तो इस उदाहरण में सबसे उपयुक्त लाइन ŷ = 47588.70+ 93.57x है

सर्वोत्तम फिट की इस पंक्ति की व्याख्या इस प्रकार करें:

• बी ₀ : जब वर्ग फुट का मूल्य शून्य है, तो अपेक्षित औसत मूल्य मूल्य $47,588.70 है। (इस मामले में वास्तव में अवरोधन की व्याख्या करने का कोई मतलब नहीं है, क्योंकि एक घर में कभी भी शून्य वर्ग फुट नहीं हो सकता)
• बी ₁ : प्रत्येक अतिरिक्त वर्ग फुट के लिए, कीमत में औसत अपेक्षित वृद्धि $93.57 है।

तो, अब हम जानते हैं कि प्रत्येक अतिरिक्त वर्ग फुट के लिए, कीमत में औसत अपेक्षित वृद्धि $93.57 है।

यह जानने के लिए कि क्या यह वृद्धि सांख्यिकीय रूप से महत्वपूर्ण है, हमें बी ₁ के लिए एक परिकल्पना परीक्षण करने या बी ₁ के लिए एक विश्वास अंतराल बनाने की आवश्यकता है।

नोट : एक परिकल्पना परीक्षण और आत्मविश्वास अंतराल हमेशा समान परिणाम देंगे।

प्रतिगमन ढलान के लिए विश्वास अंतराल का निर्माण

प्रतिगमन ढलान के लिए विश्वास अंतराल बनाने के लिए, हम निम्नलिखित सूत्र का उपयोग करते हैं:

कॉन्फिडेंस इंटरवल = b ₁ +/- (t _{1-∝/2, n-2} ) * (b ₁ की मानक त्रुटि)

सोना:

• बी ₁ प्रतिगमन परिणाम में दिया गया ढलान गुणांक है
• (t _{1-∝/2, n-2} ) स्वतंत्रता की n-2 डिग्री के साथ 1-∝ आत्मविश्वास स्तर के लिए महत्वपूर्ण t मान है जहां n हमारे डेटासेट में अवलोकनों की कुल संख्या है
• (बी ₁ की मानक त्रुटि) प्रतिगमन परिणाम में दी गई बी ₁ की मानक त्रुटि है

हमारे उदाहरण के लिए, यहां बताया गया है कि बी ₁ के लिए 95% विश्वास अंतराल कैसे बनाया जाए:

• प्रतिगमन आउटपुट से बी ₁ 93.57 है।
• चूँकि हम 95% विश्वास अंतराल का उपयोग कर रहे हैं, ∝ = 0.05 और n-2 = 12-2 = 10, इसलिए t _{0.975, 10} t वितरण तालिका के अनुसार 2.228 है
• ( _बी1 की मानक त्रुटि) प्रतिगमन आउटपुट से 11.45 है

इस प्रकार, बी ₁ के लिए हमारा 95% विश्वास अंतराल है:

93.57 +/- (2.228) * (11.45) = (68.06, 119.08)

इसका मतलब है कि हम 95% आश्वस्त हैं कि प्रत्येक अतिरिक्त वर्ग फुट के लिए वास्तविक औसत मूल्य वृद्धि $68.06 और $119.08 के बीच है।

ध्यान दें कि $0 इस अंतराल में नहीं है, इसलिए वर्ग फ़ुटेज और कीमत के बीच का संबंध 95% विश्वास स्तर पर सांख्यिकीय रूप से महत्वपूर्ण है।

प्रतिगमन ढलान के लिए एक परिकल्पना परीक्षण करना

प्रतिगमन ढलान के लिए एक परिकल्पना परीक्षण करने के लिए, हम किसी भी परिकल्पना परीक्षण के लिए पांच मानक चरणों का पालन करते हैं:

चरण 1. परिकल्पनाएँ बताएं।

शून्य परिकल्पना (H0): B ₁ = 0

वैकल्पिक परिकल्पना: (हा): बी ₁ ≠ 0

चरण 2. उपयोग करने के लिए एक महत्व स्तर निर्धारित करें।

चूँकि हमने पिछले उदाहरण में 95% विश्वास अंतराल का निर्माण किया था, हम यहाँ समतुल्य दृष्टिकोण का उपयोग करेंगे और 0.05 के महत्व स्तर का उपयोग करना चुनेंगे।

चरण 3. परीक्षण आँकड़ा और संगत पी-मान ज्ञात करें।

इस मामले में, परीक्षण आँकड़ा t = b ₁ का गुणांक / स्वतंत्रता की n-2 डिग्री के साथ b ₁ की मानक त्रुटि है। हम इन मानों को प्रतिगमन परिणाम से पा सकते हैं:

इस प्रकार, परीक्षण आँकड़ा t = 92.89 / 13.88 = 6.69।

10 डिग्री स्वतंत्रता और दो-पूंछ वाले परीक्षण के साथ 6.69 के स्कोर के साथ टी स्कोर से पी मान कैलकुलेटर का उपयोग करते हुए , पी मान = 0.000।

चरण 4. शून्य परिकल्पना को अस्वीकार करें या अस्वीकार न करें।

चूँकि पी-वैल्यू हमारे महत्व स्तर 0.05 से नीचे है, हम शून्य परिकल्पना को अस्वीकार करते हैं।

चरण 5. परिणामों की व्याख्या करें।

चूंकि हमने शून्य परिकल्पना को खारिज कर दिया है, इसलिए हमारे पास यह कहने के लिए पर्याप्त सबूत हैं कि प्रत्येक अतिरिक्त वर्ग फुट के लिए कीमत में वास्तविक औसत वृद्धि शून्य नहीं है।