बॉक्स और व्हिस्कर प्लॉट

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 5, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि बॉक्सप्लॉट, जिसे बॉक्स प्लॉट (या बॉक्सप्लॉट) के रूप में भी जाना जाता है, क्या है। आप जानेंगे कि इस प्रकार के सांख्यिकीय आरेख कैसे बनाए जाते हैं और एक बॉक्स और व्हिस्कर आरेख और इसकी व्याख्या का हल किया गया अभ्यास।

बॉक्स एंड व्हिस्कर प्लॉट क्या है?

बॉक्सप्लॉट , जिसे बॉक्सप्लॉट या बॉक्सप्लॉट भी कहा जाता है, एक ग्राफ़ है जो चतुर्थक का उपयोग करके सांख्यिकीय डेटा के एक सेट का प्रतिनिधित्व करता है।

बॉक्स और व्हिस्कर प्लॉट की मुख्य विशेषता यह है कि यह आपको डेटा की एक श्रृंखला के फैलाव की त्वरित कल्पना करने की अनुमति देता है, क्योंकि यह चतुर्थक, माध्यिका, चरम मूल्यों और डेटा के आउटलेर्स को इंगित करता है।

इस प्रकार, इस प्रकार का आरेख एक आयताकार बॉक्स और कुछ रेखाओं (या मूंछों) से बना होता है, जिसमें से निम्नलिखित मान निकलते हैं:

बॉक्स की सीमाएँ पहले और तीसरे चतुर्थक (क्यू ₁ और क्यू ₃ ) को दर्शाती हैं। और बॉक्स के अंदर की ऊर्ध्वाधर रेखा माध्यिका है (दूसरे चतुर्थक _Q2 के बराबर)।
मूंछों (या भुजाओं) की सीमाएं चरम मान हैं, यानी डेटा श्रृंखला का न्यूनतम मान और अधिकतम मान।
मूंछों के बाहर के बिंदु बाहरी हैं, या दूसरे शब्दों में, डेटा जो संभवतः गलत तरीके से मापा गया है और इसलिए सांख्यिकीय अध्ययन में इसे ध्यान में नहीं रखा जाना चाहिए।

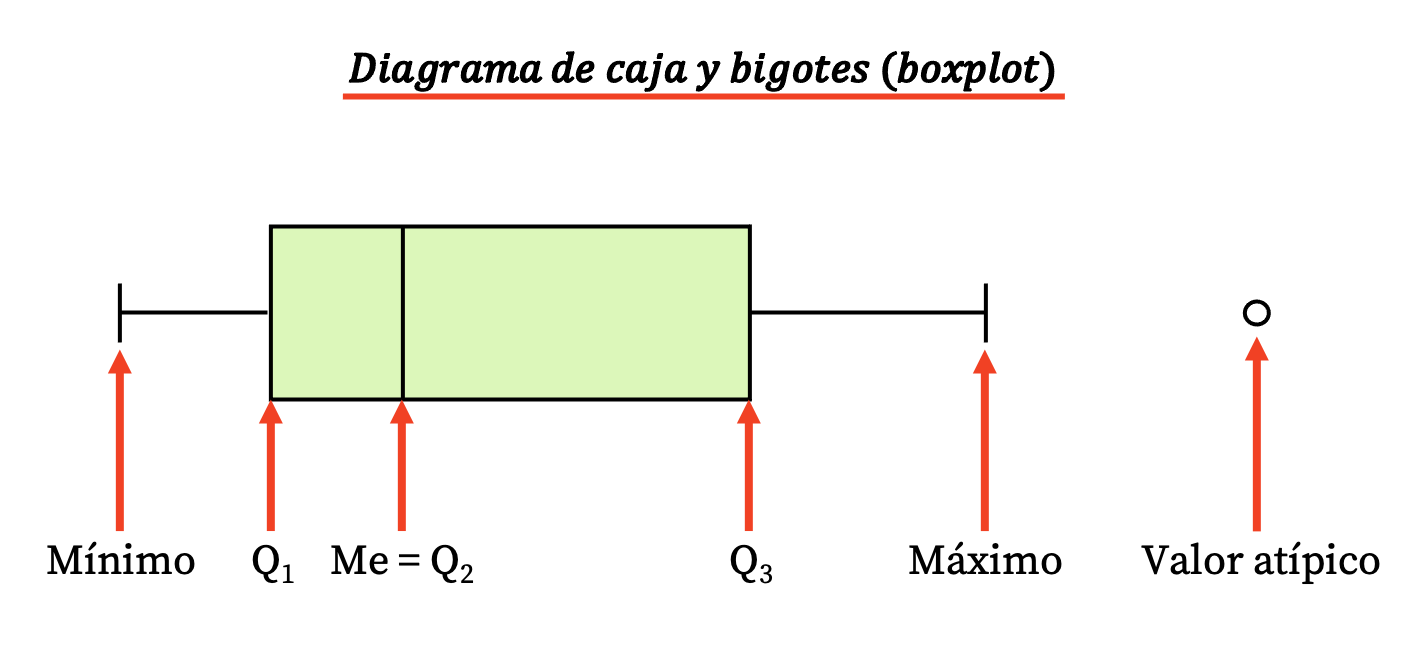
ध्यान दें कि तीसरे और पहले चतुर्थक के बीच का अंतर अंतरचतुर्थक सीमा (या इंटरचतुर्थक सीमा) है, जो सांख्यिकीय फैलाव का एक और माप है।

संख्यात्मक चरों की तुलना करने के लिए बॉक्स और व्हिस्कर प्लॉट बहुत उपयोगी होते हैं। हालाँकि, यह श्रेणीबद्ध चर का प्रतिनिधित्व करने के लिए उपयुक्त नहीं है।

बॉक्स और व्हिस्कर प्लॉट कैसे बनाएं

डेटा श्रृंखला से एक बॉक्स और व्हिस्कर प्लॉट (या बॉक्सप्लॉट) बनाने के लिए, निम्नलिखित चरणों का पालन किया जाना चाहिए:

सांख्यिकीय डेटा उदाहरणों को क्रमबद्ध करें।
चतुर्थक (क्यू ₁ , क्यू ₂ और क्यू ₃ ) की गणना करें और उन्हें आरेख में बॉक्स के रूप में दर्शाएं। पहला और तीसरा चतुर्थक बॉक्स की सीमाओं के अनुरूप है, और माध्यिका (दूसरा चतुर्थक) का प्रतिनिधित्व करने के लिए आपको बॉक्स के अंदर एक रेखा खींचनी होगी जहां इसका मान स्थित है।
अंतरचतुर्थक सीमा की गणना करें, जो प्रथम चतुर्थक को घटाकर तीसरे चतुर्थक के बराबर है।

$IQR=Q_3-Q_1$

स्वीकार्य मान LI और LS की गणना करें, जिनके सूत्र हैं:

$LI=Q_1-1,5\cdot IQR$

$LS=Q_3+1,5\cdot IQR$

नमूना आउटलेर्स की पहचान करें, जो LI से कम या LS से अधिक मान हैं। इन मानों को व्हिस्कर रेंज के बाहर बिंदुओं के साथ दर्शाएं।
चरम मूल्यों को पहचानें और उनका प्रतिनिधित्व करें, जो कि LI और LS द्वारा गठित अंतराल में सबसे छोटा मूल्य और सबसे बड़ा मूल्य है। ये मान आरेख में दो मूंछों के अंत का प्रतिनिधित्व करते हैं।

बॉक्स और व्हिस्कर प्लॉट उदाहरण

बॉक्स और व्हिस्कर प्लॉट (या बॉक्सप्लॉट) की परिभाषा और सिद्धांत पर विचार करते हुए, आपको अवधारणा को बेहतर ढंग से समझने और यह देखने के लिए एक ठोस उदाहरण नीचे मिलेगा कि इस प्रकार का सांख्यिकीय प्लॉट कैसे किया जाता है।

निम्नलिखित सांख्यिकीय डेटा सेट का एक बॉक्सप्लॉट बनाएं।

इस मामले में, डेटा पहले से ही सबसे छोटे से सबसे बड़े तक ऑर्डर किया गया है, इसलिए कोई बदलाव आवश्यक नहीं है। अन्यथा, हमें पहले नमूना डेटा को क्रमबद्ध करना चाहिए।

दूसरे, हम नमूने का चतुर्थक निकालते हैं:

$Q_1=4,06$

$Q_2=4,38$

$Q_3=4,66$

➤ देखें: चतुर्थक कैलकुलेटर

एक बार जब हम तीन चतुर्थकों की गणना कर लेते हैं, तो हम चतुर्थक 3 घटाकर चतुर्थक 1 घटाकर अंतरचतुर्थक सीमा ज्ञात करते हैं:

$IQR=Q_3-Q_1=4,66-4,06=0,6$

अब हम एलआई और एलएस सीमाओं की गणना करते हैं, जो वे मान हैं जिनसे डेटा को असामान्य माना जाता है। ऐसा करने के लिए, आपको निम्नलिखित सूत्रों का उपयोग करना होगा:

$LI=Q_1-1,5\cdot IQR=4,06-1,5\cdot 0,6=3,16$

$LS=Q_3+1,5\cdot IQR=4,66+1,5\cdot 0,6=5,56$

तो इस मामले में हमारे पास दो आउटलेयर हैं, क्योंकि 3.02, 3.16 से कम है और 5.71, 5.56 से अधिक है।

$\text{Valores at\'ipicos} =\Bigl\{3,02 \ ; \ 5,71\Bigr\}$

अंत में, यह चरम मूल्यों की पहचान करने के लिए रहता है, जो अंतराल [एलआई, एलएस] में मौजूद सभी डेटा का न्यूनतम और अधिकतम है। इसलिए, हमारे उदाहरण में, न्यूनतम मान 3.70 है और अधिकतम मान 4.81 है।

$\text{M\'inimo}=3,70$

$\text{M\'aximo}=4,81$

इसलिए, एक बार जब हमने बॉक्स और व्हिस्कर प्लॉट के सभी मूल्यों की पहचान कर ली है, तो जो कुछ बचा है वह ग्राफिकल प्रतिनिधित्व करना है:

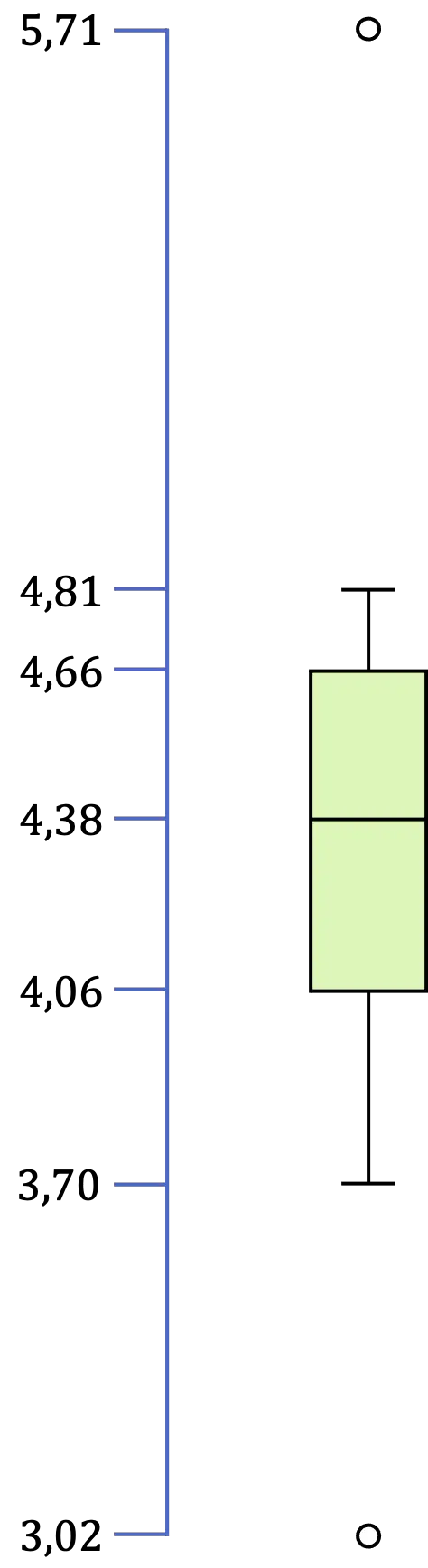
बॉक्स और व्हिस्कर प्लॉट का उपयोग किसके लिए किया जाता है?

अंत में, आइए देखें कि यह किस लिए है और बॉक्स और व्हिस्कर प्लॉट (या बॉक्सप्लॉट) की व्याख्या कैसे करें।

जाहिर है, किसी डेटा श्रृंखला के चतुर्थक, अंतरचतुर्थक श्रेणी, माध्यिका, चरम मान और आउटलेर्स को शीघ्रता से जानने के लिए बॉक्स और व्हिस्कर प्लॉट बहुत उपयोगी है, क्योंकि इन सभी सांख्यिकीय उपायों को एक साधारण दृश्य से पहचाना जा सकता है।

इसके अतिरिक्त, बॉक्स और व्हिस्कर प्लॉट का उपयोग सांख्यिकीय नमूने की समरूपता का विश्लेषण करने के लिए किया जाता है, क्योंकि यह संपूर्ण डेटा सेट का दृश्य रूप से प्रतिनिधित्व करता है। यदि माध्यिका बॉक्स के केंद्र में नहीं है, तो इसका मतलब है कि नमूना सममित नहीं है।

इसी तरह, स्टॉक मार्केट में समय की अवधि में स्टॉक की कीमत में भिन्नता का प्रतिनिधित्व करने के लिए बॉक्सप्लॉट का व्यापक रूप से उपयोग किया जाता है, क्योंकि वे किसी को कम समय में अधिकतम मूल्य, न्यूनतम मूल्य और मध्यवर्ती मूल्यों को देखने की अनुमति देते हैं। समय और इस प्रकार तेजी से निर्णय लें।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने