सांख्यिकी में पूर्वानुमान त्रुटि क्या है? (परिभाषा एवं उदाहरण)
आँकड़ों में, पूर्वानुमान त्रुटि का तात्पर्य कुछ मॉडलों द्वारा अनुमानित मूल्यों और वास्तविक मूल्यों के बीच अंतर से है।
पूर्वानुमान त्रुटि का प्रयोग अक्सर दो संदर्भों में किया जाता है:
1. रैखिक प्रतिगमन: निरंतर प्रतिक्रिया चर के मूल्य की भविष्यवाणी करने के लिए उपयोग किया जाता है।
हम आम तौर पर आरएमएसई नामक मीट्रिक के साथ एक रैखिक प्रतिगमन मॉडल की भविष्यवाणी त्रुटि को मापते हैं, जो मूल माध्य वर्ग त्रुटि के लिए है।
इसकी गणना इस प्रकार की जाती है:
RMSE = √ Σ(ŷ i – y i ) 2 / n
सोना:
- Σ एक प्रतीक है जिसका अर्थ है “योग”
- ŷ i, i वें अवलोकन के लिए अनुमानित मान है
- y i, iवें अवलोकन के लिए प्रेक्षित मान है
- n नमूना आकार है
2. लॉजिस्टिक रिग्रेशन: बाइनरी प्रतिक्रिया चर के मूल्य की भविष्यवाणी करने के लिए उपयोग किया जाता है।
लॉजिस्टिक रिग्रेशन मॉडल की भविष्यवाणी त्रुटि को मापने का एक सामान्य तरीका कुल वर्गीकरण त्रुटि दर के रूप में ज्ञात मीट्रिक का उपयोग करना है।
इसकी गणना इस प्रकार की जाती है:
कुल ग़लत वर्गीकरण दर = (# गलत भविष्यवाणियाँ / # कुल भविष्यवाणियाँ)
गलत वर्गीकरण दर का मूल्य जितना कम होगा, मॉडल प्रतिक्रिया चर के परिणामों की भविष्यवाणी करने में उतना ही बेहतर सक्षम होगा।
निम्नलिखित उदाहरण दिखाते हैं कि व्यवहार में एक रैखिक प्रतिगमन मॉडल और एक लॉजिस्टिक प्रतिगमन मॉडल के लिए भविष्यवाणी त्रुटि की गणना कैसे करें।
उदाहरण 1: रैखिक प्रतिगमन में भविष्यवाणी त्रुटि की गणना
मान लीजिए कि हम एक प्रतिगमन मॉडल का उपयोग यह अनुमान लगाने के लिए करते हैं कि बास्केटबॉल खेल में 10 खिलाड़ी कितने अंक अर्जित करेंगे।
निम्न तालिका खिलाड़ियों द्वारा प्राप्त वास्तविक अंकों की तुलना में मॉडल द्वारा अनुमानित अंकों को दर्शाती है:

हम मूल माध्य वर्ग त्रुटि (RMSE) की गणना इस प्रकार करेंगे:
- RMSE = √ Σ(ŷ i – y i ) 2 / n
- आरएमएसई = √(((14-12) 2 +(15-15) 2 +(18-20) 2 +(19-16) 2 +(25-20) 2 +(18-19) 2 +(12- 16) 2 +(12-20) 2 +(15-16) 2 +(22-16) 2 )/10)
- आरएमएसई = 4
माध्य वर्ग त्रुटि 4 है। यह हमें बताता है कि अनुमानित अंक और प्राप्त वास्तविक अंक के बीच औसत विचलन 4 है।
संबंधित: एक अच्छा आरएमएसई मूल्य क्या माना जाता है?
उदाहरण 2: लॉजिस्टिक रिग्रेशन में भविष्यवाणी त्रुटि की गणना
मान लीजिए कि हम यह अनुमान लगाने के लिए एक लॉजिस्टिक रिग्रेशन मॉडल का उपयोग करते हैं कि 10 कॉलेज बास्केटबॉल खिलाड़ियों को एनबीए में शामिल किया जाएगा या नहीं।
निम्नलिखित तालिका प्रत्येक खिलाड़ी के लिए अनुमानित परिणाम बनाम वास्तविक परिणाम दिखाती है (1 = प्रारूपित, 0 = अप्रकाशित):
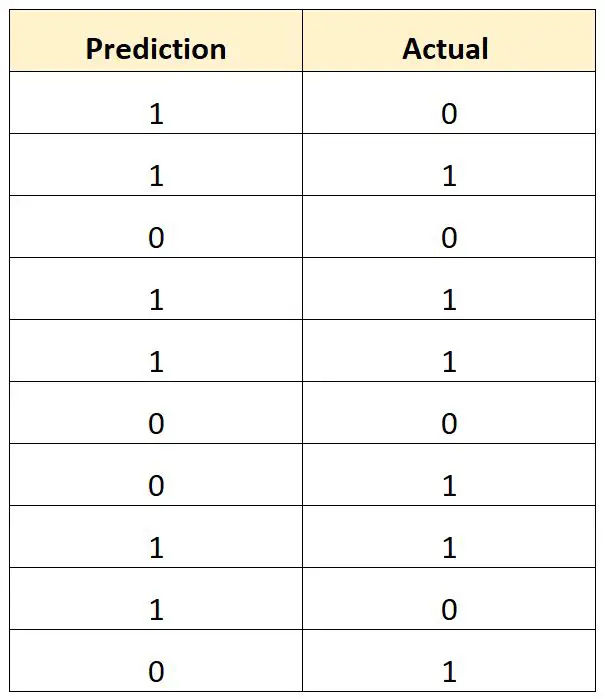
हम कुल गलत वर्गीकरण दर की गणना इस प्रकार करेंगे:
- कुल ग़लत वर्गीकरण दर = (# गलत भविष्यवाणियाँ / # कुल भविष्यवाणियाँ)
- कुल वर्गीकरण त्रुटि दर = 4/10
- कुल गलत वर्गीकरण दर = 40%
कुल वर्गीकरण त्रुटि दर 40% है।
यह मान काफी अधिक है, जो दर्शाता है कि मॉडल यह भविष्यवाणी करने में बहुत अच्छा काम नहीं कर रहा है कि किसी खिलाड़ी को ड्राफ्ट किया जाएगा या नहीं।
अतिरिक्त संसाधन
निम्नलिखित ट्यूटोरियल विभिन्न प्रकार के प्रतिगमन विधियों का परिचय प्रदान करते हैं:
सरल रेखीय प्रतिगमन का परिचय
एकाधिक रेखीय प्रतिगमन का परिचय
लॉजिस्टिक रिग्रेशन का परिचय