भारित औसत

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 6, 2023 आंकड़े शून्य टिप्पणियां

यहां हम बताते हैं कि भारित औसत क्या है और इसकी गणना कैसे की जाती है। आप एक हल किया गया अभ्यास देख पाएंगे कि हम भारित औसत कैसे ज्ञात करते हैं। और, इससे भी अधिक, आप अंत में कैलकुलेटर के साथ किसी भी डेटा सेट के भारित औसत की गणना कर सकते हैं।

भारित औसत क्या है?

भारित औसत वर्णनात्मक आँकड़ों की केंद्रीयता का एक माप है। भारित औसत की गणना करने के लिए, आपको पहले प्रत्येक सांख्यिकीय डेटा को उसके वजन (या वजन) से गुणा करना होगा, फिर सभी उत्पादों को जोड़ना होगा, और अंत में भारित योग को सभी भारों के योग से विभाजित करना होगा।

दूसरे शब्दों में, भारित औसत का सूत्र इस प्रकार है:

जहां x _i प्रत्येक डेटा नमूने का प्रतिनिधित्व करता है और w _i उसके संबंधित वजन का प्रतिनिधित्व करता है।

इस प्रकार, डेटा के एक टुकड़े का वजन जितना अधिक होगा, भारित औसत की गणना में यह उतना ही महत्वपूर्ण हो जाता है। दूसरे शब्दों में, डेटा के एक टुकड़े का भार जितना अधिक होगा, यह भारित औसत के परिणाम को उतना ही अधिक प्रभावित करेगा।

भारित औसत ग्रेड की गणना के लिए विशेष रूप से उपयोगी है, क्योंकि यह आपको पाठ्यक्रम के दौरान किए गए अभ्यासों या परीक्षाओं का अलग-अलग महत्व के साथ मूल्यांकन करने की अनुमति देता है। भारित औसत का उपयोग सीपीआई (उपभोक्ता मूल्य सूचकांक) की गणना के लिए भी किया जाता है, जो जनसंख्या की कीमतों को मापने के लिए एक संकेतक है।

भारित औसत के अलावा, अन्य प्रकार के औसत भी होते हैं जैसे ज्यामितीय औसत, अंकगणितीय औसत, वर्ग औसत और हार्मोनिक औसत।

भारित औसत की गणना कैसे करें

भारित औसत की गणना करने के लिए, निम्नलिखित चरणों का पालन किया जाना चाहिए:

प्रत्येक सांख्यिकीय डेटा को उसके संगत भार से गुणा करें।
पिछले चरण में गणना किए गए सभी उत्पादों को जोड़ें।
उपरोक्त भारित योग को सभी भारों के योग से विभाजित करें।
प्राप्त परिणाम सांख्यिकीय नमूने का भारित औसत है।

👉 आप किसी भी डेटा सेट के भारित औसत की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।

भारित औसत उदाहरण

भारित औसत की परिभाषा पर विचार करते हुए, अब हम पूरी तरह से समझने के लिए एक अभ्यास को हल करेंगे कि डेटा के एक सेट से भारित औसत कैसे प्राप्त किया जाता है।

हाई स्कूल के प्रथम वर्ष के एक छात्र ने गणित विषय में निम्नलिखित ग्रेड प्राप्त किए: आंशिक परीक्षा में 7 अंक जो 30% के बराबर है, समूह कार्य पर 9 अंक जो 20% के बराबर है, कक्षा में दिए गए अभ्यासों पर 6 अंक, भारांक के साथ 10% का और अंतिम परीक्षा में 8 अंक का वेटेज 40% है। विषय के लिए आपका अंतिम ग्रेड क्या है?

छात्र के अंक निर्धारित करने के लिए, आपको कथन द्वारा दिए गए मानों के साथ भारित औसत ज्ञात करना होगा। ऐसा करने के लिए, हम भारित औसत सूत्र लागू करते हैं:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+x_3\cdot w_3+x_4\cdot w_4+x_5\cdot w_5}{w_1+w_2+w_3+w_4+w_5}$

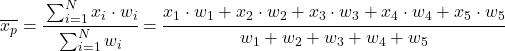
प्रत्येक डिलिवरेबल का स्कोर सांख्यिकीय मूल्य है और इसका प्रतिशत उक्त मूल्य के वजन से मेल खाता है। इसलिए, हम मानों और भारों को सूत्र में प्रतिस्थापित करते हैं और भारित औसत गणना करते हैं:

$\overline{x_p}=\cfrac{7\cdot 0,30+9\cdot 0,20+6\cdot 0,10+8\cdot 0,40}{0,30+0,20+0,10+0,40}=7,7$

इसलिए इस छात्र का अंतिम गणित ग्रेड 7.7 होगा क्योंकि यह भारित औसत से प्राप्त परिणाम है।

भारित औसत कैलकुलेटर

इसके भारित औसत की गणना करने के लिए नीचे दिए गए कैलकुलेटर में किसी भी सांख्यिकीय नमूने से डेटा और उनके संबंधित वजन दर्ज करें।

पहले बॉक्स में सांख्यिकीय डेटा और दूसरे बॉक्स में उनके संबंधित वजन दर्ज करें। आपको वज़न को डेटा के समान क्रम में और दशमलव प्रारूप में लिखना होगा। सभी संख्याओं को एक स्थान से अलग किया जाना चाहिए और दशमलव विभाजक के रूप में अवधि का उपयोग करके दर्ज किया जाना चाहिए।

मानकीकृत वजन

जैसा कि हमने देखा है, भारित औसत में, वजन वह मूल्य है जो डेटा के प्रत्येक टुकड़े को कम या ज्यादा महत्व देने के लिए दिया जाता है। इसलिए, यदि जानकारी बहुत महत्वपूर्ण है, तो इसका महत्व बहुत अधिक होगा, लेकिन यदि जानकारी बहुत प्रासंगिक नहीं है, तो इसका महत्व बहुत कम होगा।

खैर, सामान्यीकृत वजन एक प्रकार का भार है जिसका उपयोग बिना किसी विभाजन के भारित औसत प्राप्त करने के लिए किया जाता है।

सामान्यीकृत वजन किसी डेटा आइटम के वजन को सभी वजनों के योग से विभाजित करने पर प्राप्त होता है।

$w_i'=\cfrac{w_i}{\sum_{k=1}^N w_k}$

इसलिए सभी सामान्यीकृत भारों का योग एक के बराबर है:

$\sum_{i=1}^N w_i'=1$

तो, सामान्यीकृत वजन के साथ भारित औसत की गणना करने के लिए, बस प्रत्येक डेटा आइटम को उसके सामान्यीकृत वजन से गुणा करें:

$\displaystyle\overline{x_p}=\sum_{i=1}^N x_i\cdot w_i'=x_1\cdot w_1'+x_2\cdot w_2'+\dots+x_N\cdot w_N'$

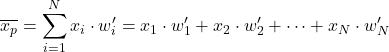
उदाहरण के लिए, हमारे पास एक सांख्यिकीय नमूना है जिसका डेटा 24, 35, 17, 41 है और उनके संबंधित वजन 4, 9, 6, 3 हैं। इस डेटा सेट का भारित औसत ज्ञात करने के लिए, हम पहले विभाजित करके सामान्यीकृत वजन की गणना कर सकते हैं सभी भारों के योग से प्रत्येक भार:

$\cfrac{4}{4+9+6+3}=0,18$

$\cfrac{9}{4+9+6+3}=0,41$

$\cfrac{6}{4+9+6+3}=0,27$

$\cfrac{3}{4+9+6+3}=0,14$

और अब बस प्रत्येक डेटा को उसके सामान्यीकृत वजन से गुणा करें और परिणाम भारित औसत होगा:

$\overline{x_p}=24\cdot 0,18+35\cdot 0,41+17\cdot 0,27+41\cdot 0,14=28,91$

भारित औसत और अंकगणितीय औसत के बीच अंतर

भारित औसत और अंकगणितीय औसत की गणना एक ही तरह से की जाती है, क्योंकि समान संचालन किया जाना चाहिए। भारित औसत में, प्रत्येक डेटा बिंदु को उसके वजन से गुणा किया जाता है और वजन के योग से विभाजित किया जाता है, लेकिन अंकगणितीय औसत में, सभी डेटा को एक साथ जोड़ा जाता है और डेटा बिंदुओं की कुल संख्या से विभाजित किया जाता है।

भारित औसत और अंकगणितीय औसत के बीच का अंतर इसकी अवधारणा में निहित है, क्योंकि अंकगणितीय औसत में यह माना जाता है कि सभी डेटा का मूल्य समान है, हालांकि, भारित औसत में प्रत्येक डेटा का अलग-अलग वजन होता है।

ध्यान दें कि यदि सभी भार समान हैं, तो भारित औसत अंकगणितीय औसत के बराबर है। आप गणितीय प्रमाण नीचे देख सकते हैं:

$\begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}$

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने