भिन्नता के लिए परिकल्पना परीक्षण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि विचरण के लिए परिकल्पना परीक्षण क्या है। तो, आपको विचरण परिकल्पना परीक्षण के लिए सूत्र मिलेगा और इसके अलावा, चरण दर चरण हल किया गया एक अभ्यास भी मिलेगा।

विचरण के लिए परिकल्पना परीक्षण क्या है?

विचरण के लिए परिकल्पना परीक्षण एक सांख्यिकीय पद्धति है जिसका उपयोग यह निर्धारित करने के लिए किया जाता है कि जनसंख्या विचरण की शून्य परिकल्पना को अस्वीकार किया जाए या नहीं। दूसरे शब्दों में, विचरण परिकल्पना परीक्षण का उपयोग किसी जनसंख्या के विचरण के मूल्य के बारे में परिकल्पना को अस्वीकार करने या स्वीकार करने के लिए किया जाता है।

विशेष रूप से, विचरण के लिए परिकल्पना परीक्षण आंकड़ों के मूल्य और चुने गए महत्व स्तर के आधार पर, शून्य परिकल्पना को अस्वीकार या स्वीकार कर लिया जाता है।

ध्यान रखें कि परिकल्पना परीक्षण को कई नामों से जाना जाता है, इसे परिकल्पना विरोधाभास, परिकल्पना परीक्षण या महत्व परीक्षण भी कहा जा सकता है।

भिन्नता के लिए परिकल्पना परीक्षण सूत्र

विचरण के लिए परिकल्पना परीक्षण आँकड़ा नमूना आकार के बीच के अंतर को नमूना विचरण के एक गुना से घटाकर जनसंख्या विचरण के प्रस्तावित मूल्य से विभाजित करने के बराबर है। विचरण के लिए परिकल्पना परीक्षण आँकड़ा में काई-वर्ग वितरण होता है।

इस प्रकार, विचरण के लिए परिकल्पना परीक्षण आँकड़ा की गणना करने का सूत्र इस प्रकार है:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

सोना:

$\chi^2$

विचरण के लिए परिकल्पना परीक्षण आँकड़ा है, जिसमें काई-स्क्वायर वितरण होता है।
$n$

नमूना आकार है.
$s^2$

नमूना विचरण है.
$\sigma^2$

प्रस्तावित जनसंख्या भिन्नता है।

आंकड़ों के परिणाम की व्याख्या करने के लिए, प्राप्त मूल्य की तुलना परीक्षण के महत्वपूर्ण मूल्य से की जानी चाहिए।

यदि विचरण के लिए परिकल्पना परीक्षण दो-पुच्छीय है, तो यदि आँकड़ा महत्वपूर्ण मान से अधिक है, तो शून्य परिकल्पना खारिज कर दी जाती है।
$\chi_{1-\alpha/2|n-1}^2$

या यदि क्रांतिक मान इससे कम है

$\chi_{\alpha/2|n-1}$

.
यदि विचरण के लिए परिकल्पना परीक्षण सही पूंछ से मेल खाता है, तो शून्य परिकल्पना खारिज कर दी जाती है यदि आँकड़ा महत्वपूर्ण मूल्य से अधिक है
$\chi_{1-\alpha|n-1}^2$

.
यदि विचरण के लिए परिकल्पना परीक्षण बाईं पूंछ से मेल खाता है, तो शून्य परिकल्पना खारिज कर दी जाती है यदि आँकड़ा महत्वपूर्ण मूल्य से कम है
$\chi_{\alpha|n-1}$

.

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

विचरण के लिए महत्वपूर्ण परिकल्पना परीक्षण मान ची-स्क्वायर वितरण तालिका से प्राप्त किए जाते हैं। ध्यान दें कि ची-स्क्वायर वितरण के लिए स्वतंत्रता की डिग्री नमूना आकार शून्य से 1 है।

भिन्नता के लिए परिकल्पना परीक्षण का वास्तविक-विश्व उदाहरण

विचरण परिकल्पना परीक्षण की परिभाषा और इसका सूत्र क्या है, यह देखने के बाद, हम अवधारणा को आत्मसात करने के लिए एक ठोस उदाहरण देखेंगे।

एक कारखाने में एक मशीन होती है जो उच्च परिशुद्धता के साथ कार के लिए पुर्जे बनाती है। हालाँकि, यह संदेह है कि यह दूर चला गया है और अब 8 मिमी ² से अधिक अंतर वाले भागों का निर्माण करता है। इस परिकल्पना का खंडन करने के लिए, 25 टुकड़ों के एक नमूने का विश्लेषण किया गया है और इसका नमूना भिन्नता 9.1 मिमी ² है। क्या प्रारंभिक परिकल्पना को महत्व स्तर α=0.05 के साथ खारिज किया जा सकता है?

इस विचरण परिकल्पना परीक्षण के लिए शून्य परिकल्पना और वैकल्पिक परिकल्पना इस प्रकार हैं:

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}” title=”Rendered by QuickLaTeX.com” height=”65″ width=”101″ style=”vertical-align: 0px;”> यह निर्धारित करने के लिए कि शून्य परिकल्पना को अस्वीकार किया जा सकता है या नहीं, हम ऊपर देखे गए सूत्र का उपयोग करके भिन्नता के लिए परिकल्पना परीक्षण आंकड़ों की गणना करते हैं: <p class=$ $\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

अब हम ची-स्क्वायर वितरण तालिका में 24 डिग्री स्वतंत्रता और महत्व स्तर α=0.05 के लिए दाहिनी पूंछ के अनुरूप महत्वपूर्ण मान की तलाश करते हैं:

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

इस प्रकार, परिकलित आँकड़ा परीक्षण के महत्वपूर्ण मान से कम है और इसलिए विचरण परिकल्पना परीक्षण की शून्य परिकल्पना को अस्वीकार नहीं किया जाता है, बल्कि वैकल्पिक परिकल्पना को अस्वीकार कर दिया जाता है।

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤ देखें: जनसंख्या माध्य के लिए परिकल्पना परीक्षण
➤ देखें: जनसंख्या अनुपात के लिए परिकल्पना परीक्षण

दो आबादी के विचरण के लिए परिकल्पना परीक्षण

दो-जनसंख्या विचरण परिकल्पना परीक्षण का उपयोग उस परिकल्पना को अस्वीकार या स्वीकार करने के लिए किया जाता है कि दो अलग-अलग आबादी के प्रसरण बराबर हैं।

इस प्रकार दो आबादी के विचरण पर एक परिकल्पना परीक्षण की शून्य परिकल्पना हमेशा निम्नलिखित होती है:

$H_0: \sigma^2_1=\sigma^2_2$

और वैकल्पिक परिकल्पना तीन विकल्पों में से एक हो सकती है:

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

इस मामले में, दो आबादी के विचरण के लिए परिकल्पना परीक्षण आंकड़ों की गणना करने का सूत्र है:

$F=\cfrac{s_1^2}{s_2^2}$

सोना:

$F$

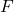
दो आबादी के विचरण के लिए परिकल्पना परीक्षण आँकड़ा है, जो एफ वितरण का अनुसरण करता है।
$\sigma_1^2$

जनसंख्या 1 का प्रसरण है।
$\sigma_2^2$

जनसंख्या 2 का प्रसरण है।
$s_1^2$

नमूना 1 का भिन्नता है.
$s_2^2$

नमूना 2 का विचरण है।
$n_1$

नमूना आकार 1 है.
$n_2$

नमूना आकार 2 है.

चूंकि स्नेडेकोर एफ वितरण सममित नहीं है, इसलिए शून्य परिकल्पना को निम्नलिखित मानदंडों के आधार पर खारिज कर दिया गया है:

[लेटेक्स]\begin{array}{l}H_1: \sigma_1^2\neq \sigma_2^2 \ \color{नारंगी}\bm{\longrightarrow}\color{black} \ \text{Si } F>F_{ 1-\alpha/2|n_1-1|n_2-1}\text{ से rechaza } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{नारंगी}\bm{\longrightarrow }\रंग{काला} \\पाठ{यदि }एफ \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{If } F>F_{1-\alpha|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \ \color{नारंगी}\bm{\longrightarrow}\color{black} \ \text{Si } F

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने