जड़ का अर्थ है वर्गाकार

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 6, 2023 आंकड़े शून्य टिप्पणियां

यहां हम बताते हैं कि मूल माध्य वर्ग क्या है और इसकी गणना कैसे की जाती है। इसके अलावा, आप औसत और चरण-दर-चरण हल किए गए अभ्यास का उपयोग करने के फायदे और नुकसान सीखेंगे। अंत में, आप लेख के अंत में कैलकुलेटर के साथ किसी भी डेटा सेट के मूल माध्य वर्ग की गणना करने में सक्षम होंगे।

माध्य वर्ग क्या है?

मूल माध्य वर्ग वर्णनात्मक आँकड़ों की केंद्रीयता का एक माप है। मूल माध्य वर्ग डेटा के वर्गों के अंकगणितीय माध्य के वर्गमूल के बराबर है।

मूल माध्य वर्ग को मूल माध्य वर्ग या आरएमएस भी कहा जाता है।

इसलिए द्विघात माध्य का सूत्र इस प्रकार है:

वर्ग माध्य विशेष रूप से तब उपयोगी होता है जब सांख्यिकीय चर सकारात्मक और नकारात्मक मान लेता है, क्योंकि डेटा के प्रत्येक टुकड़े का वर्ग करने से सभी मान सकारात्मक हो जाते हैं। इसलिए, माध्य वर्ग का उपयोग उन चरों का विश्लेषण करने के लिए किया जाता है जिनमें चिह्न महत्वपूर्ण नहीं है, बल्कि उसका निरपेक्ष मान महत्वपूर्ण है।

उदाहरण के लिए, माध्य वर्ग का उपयोग माप त्रुटियों का अध्ययन करने के लिए किया जाता है, क्योंकि इन मामलों में हम यह नहीं देख रहे हैं कि त्रुटि सकारात्मक है या नकारात्मक, बल्कि मापते समय त्रुटि की भयावहता का विश्लेषण कर रहे हैं।

इसके अतिरिक्त, बड़ी संख्याओं के वर्गों का मान छोटी संख्याओं के वर्गों की तुलना में बहुत अधिक होता है, इसलिए मध्य वर्ग में छोटी संख्याओं की तुलना में बड़ी संख्याएँ अधिक महत्वपूर्ण होती हैं।

वर्ग माध्य अंकगणितीय माध्य, भारित माध्य, ज्यामितीय माध्य और हार्मोनिक माध्य के साथ एक प्रकार का सांख्यिकीय औसत है।

मूल माध्य वर्ग के फायदे और नुकसान

अन्य प्रकार के औसत की तुलना में द्विघात औसत के फायदे और नुकसान हैं।

द्विघात माध्य का मुख्य लाभ यह है कि यह आपको एक अलग चर के औसत मूल्य का बहुत अच्छा अनुमान प्राप्त करने की अनुमति देता है। दूसरी ओर, वर्ग औसत का बड़ा नुकसान यह है कि इसकी गणना काफी जटिल है, क्योंकि कई ऑपरेशन करने पड़ते हैं।

इसके विपरीत, त्रुटि माप का विश्लेषण करने के लिए मूल माध्य वर्ग बहुत उपयोगी है। यह उच्च मूल्यों को भी अधिक महत्व देता है, हालांकि इस संपत्ति का तात्पर्य है कि एक गलत माप आरएमएस परिणाम को महत्वपूर्ण रूप से बदल देगा।

मूल माध्य वर्ग की गणना कैसे करें

मूल माध्य वर्ग की गणना करने के लिए, निम्नलिखित चरणों का पालन किया जाना चाहिए:

प्रत्येक सांख्यिकीय डेटा के वर्ग की गणना करें।
पिछले चरण में गणना किए गए सभी वर्गों को जोड़ें।
परिणाम को नमूने में डेटा आइटम की संख्या से विभाजित करें।
पिछले मान का वर्गमूल ज्ञात कीजिए।
प्राप्त परिणाम सांख्यिकीय नमूने का वर्ग माध्य है।

👉 आप किसी भी डेटा सेट के मूल माध्य वर्ग की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।

माध्य वर्ग उदाहरण

एक बार जब हम जान जाते हैं कि मूल माध्य वर्ग कैसे प्राप्त किया जाता है, तो हम एक उदाहरण के रूप में डेटा के एक सेट का मूल माध्य वर्ग निर्धारित करेंगे।

एक विश्वविद्यालय प्रयोगशाला कक्षा में, प्रोफेसर अपने छात्रों से रसायनों के साथ एक प्रयोग करने के लिए कहता है। रासायनिक प्रयोग का लक्ष्य कुल 3 लीटर का घोल प्राप्त करना है। छात्र समूहों ने निम्नलिखित डेटा प्राप्त किया:

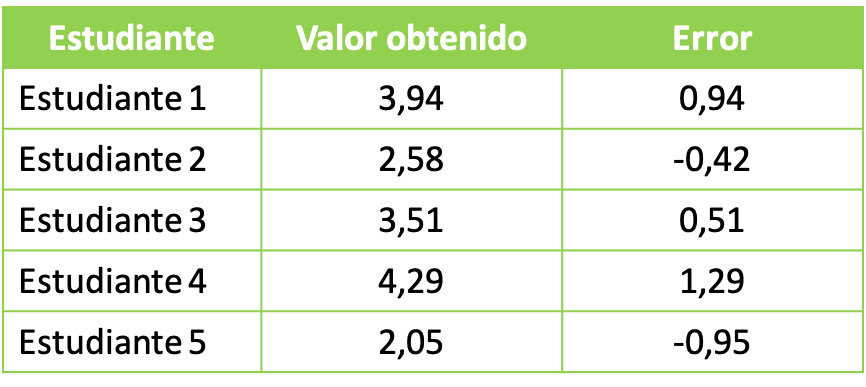
प्राप्त सांख्यिकीय आंकड़ों का अध्ययन करने के लिए, हम प्रत्येक समूह द्वारा प्राप्त त्रुटि के साथ वर्ग माध्य के मान की गणना करने के लिए आगे बढ़ते हैं। इसलिए हम द्विघात माध्य सूत्र लागू करते हैं:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

और हम डेटा को सूत्र में प्रतिस्थापित करते हैं और मूल माध्य वर्ग की गणना करते हैं:

$\displaystyle RMS=\sqrt{\frac{0,94^2+(-0,42)^2+0,51^2+1,29^2+(-0,95)^2}{5}}=0,88$

इस प्रकार, प्रयोग में प्राप्त औसत त्रुटि, मूल माध्य वर्ग के अनुसार, 0.88 लीटर है।

माध्य वर्ग कैलकुलेटर

किसी भी सांख्यिकीय नमूने से उसके मूल माध्य वर्ग की गणना करने के लिए निम्नलिखित कैलकुलेटर में डेटा दर्ज करें। डेटा को एक स्थान से अलग किया जाना चाहिए और दशमलव विभाजक के रूप में अवधि का उपयोग करके दर्ज किया जाना चाहिए।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने