एसपीएसएस में लेवेने टेस्ट कैसे करें

लेवेने परीक्षण का उपयोग यह निर्धारित करने के लिए किया जाता है कि क्या दो या दो से अधिक समूहों में समान भिन्नताएँ हैं।

इसका व्यापक रूप से उपयोग किया जाता है क्योंकि कई सांख्यिकीय परीक्षण इस धारणा पर निर्भर करते हैं कि समूहों में समान भिन्नताएँ होती हैं।

यह ट्यूटोरियल बताता है कि एसपीएसएस में लेवेने परीक्षण कैसे करें।

उदाहरण: एसपीएसएस में लेवेने परीक्षण

शोधकर्ता जानना चाहते हैं कि क्या तीन अलग-अलग उर्वरकों से पौधों की वृद्धि का स्तर अलग-अलग होता है।

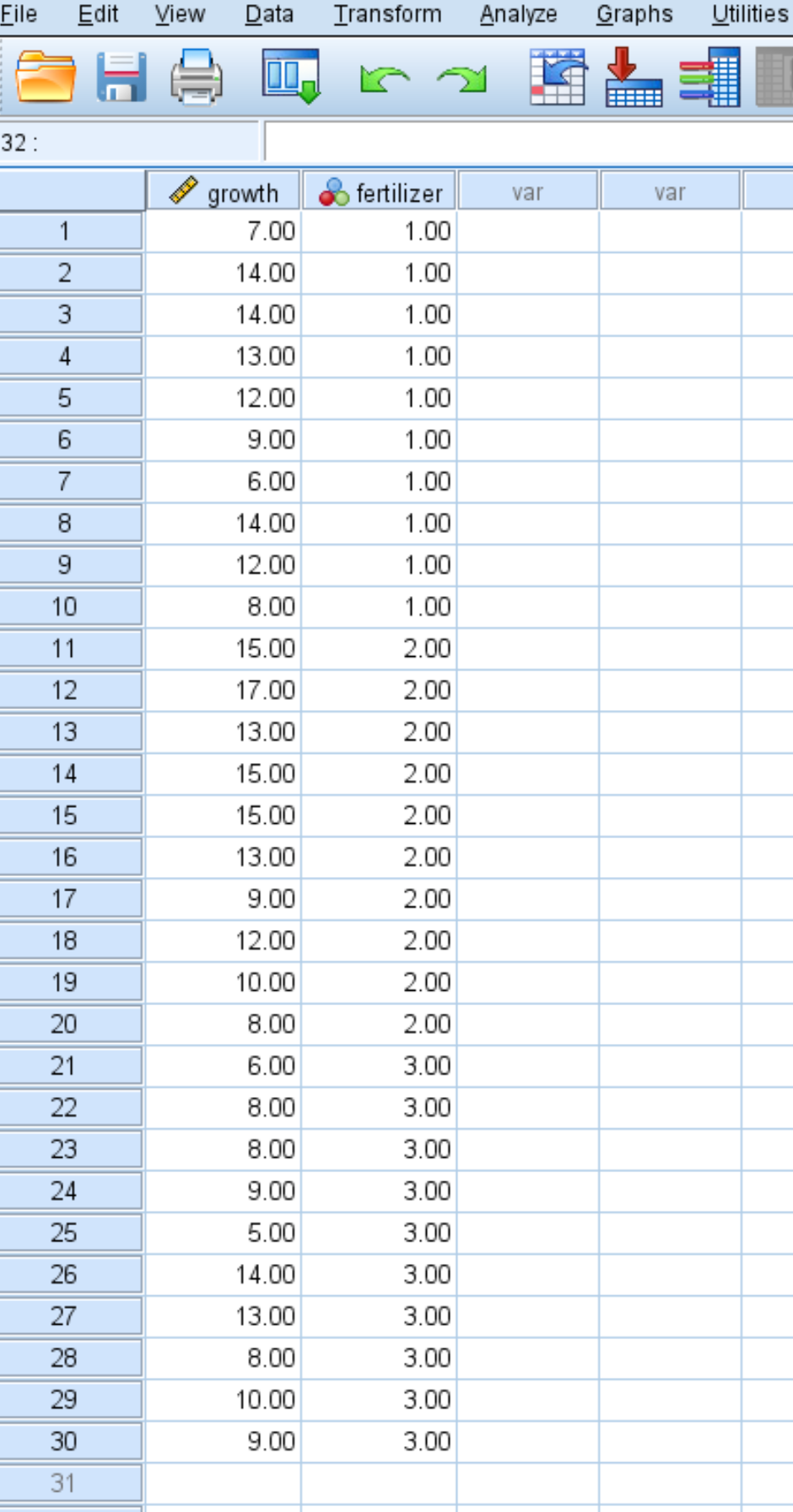
वे बेतरतीब ढंग से 30 अलग-अलग पौधों का चयन करते हैं और उन्हें 10 के तीन समूहों में विभाजित करते हैं, प्रत्येक समूह में एक अलग उर्वरक डालते हैं। एक महीने के बाद, वे प्रत्येक पौधे की ऊंचाई मापते हैं।

निम्नलिखित स्क्रीनशॉट प्रत्येक पौधे के लिए वृद्धि की मात्रा (इंच में) दिखाता है, साथ ही पौधे पर लागू उर्वरक (1, 2, या 3) भी दिखाता है:

यह निर्धारित करने के लिए कि तीन समूहों में समान भिन्नताएं हैं या नहीं, एसपीएसएस में लेवेने का परीक्षण करने के लिए निम्नलिखित चरणों का पालन करें।

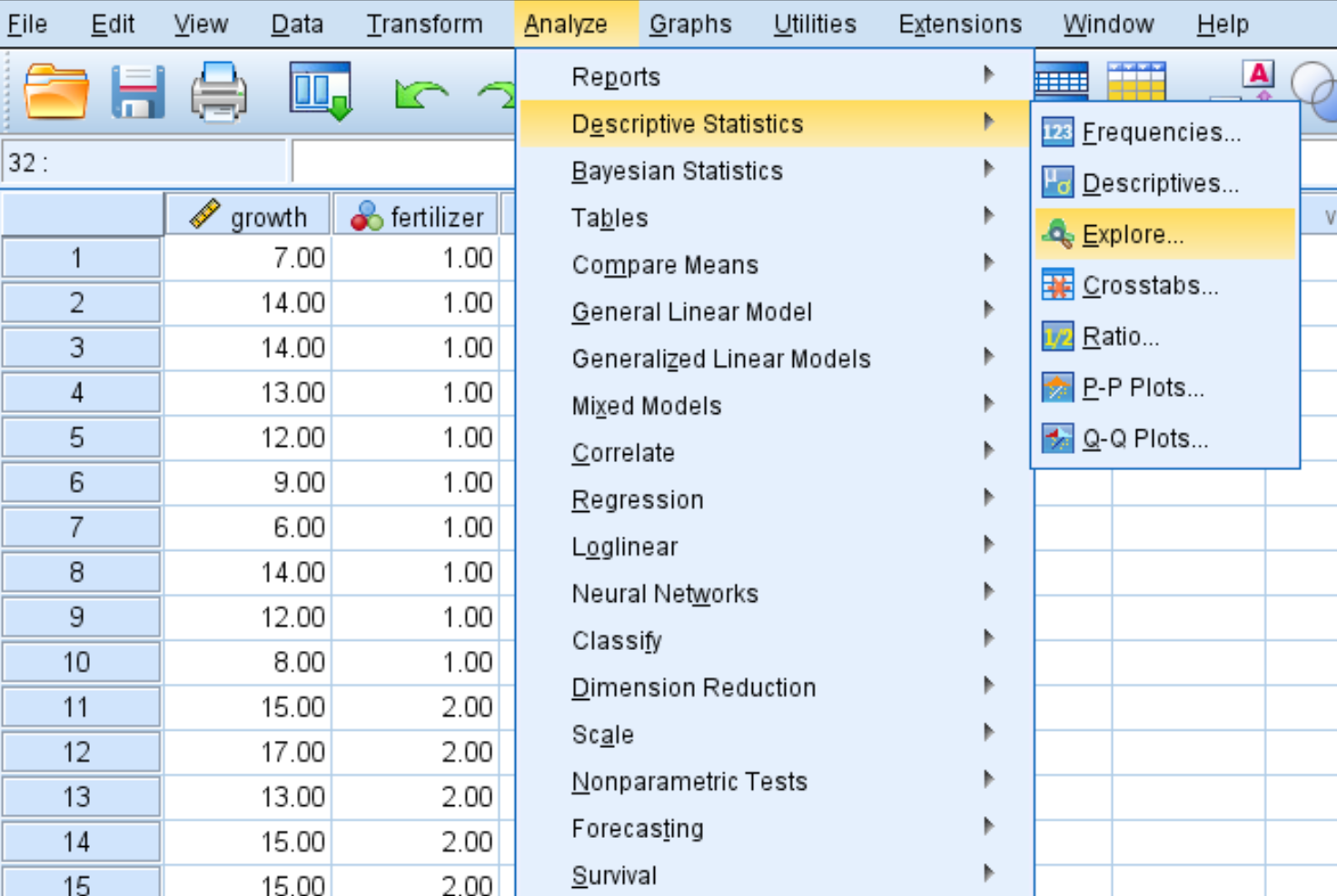
चरण 1: एक्सप्लोर विकल्प चुनें।

विश्लेषण टैब पर क्लिक करें, फिर वर्णनात्मक सांख्यिकी , फिर अन्वेषण करें :

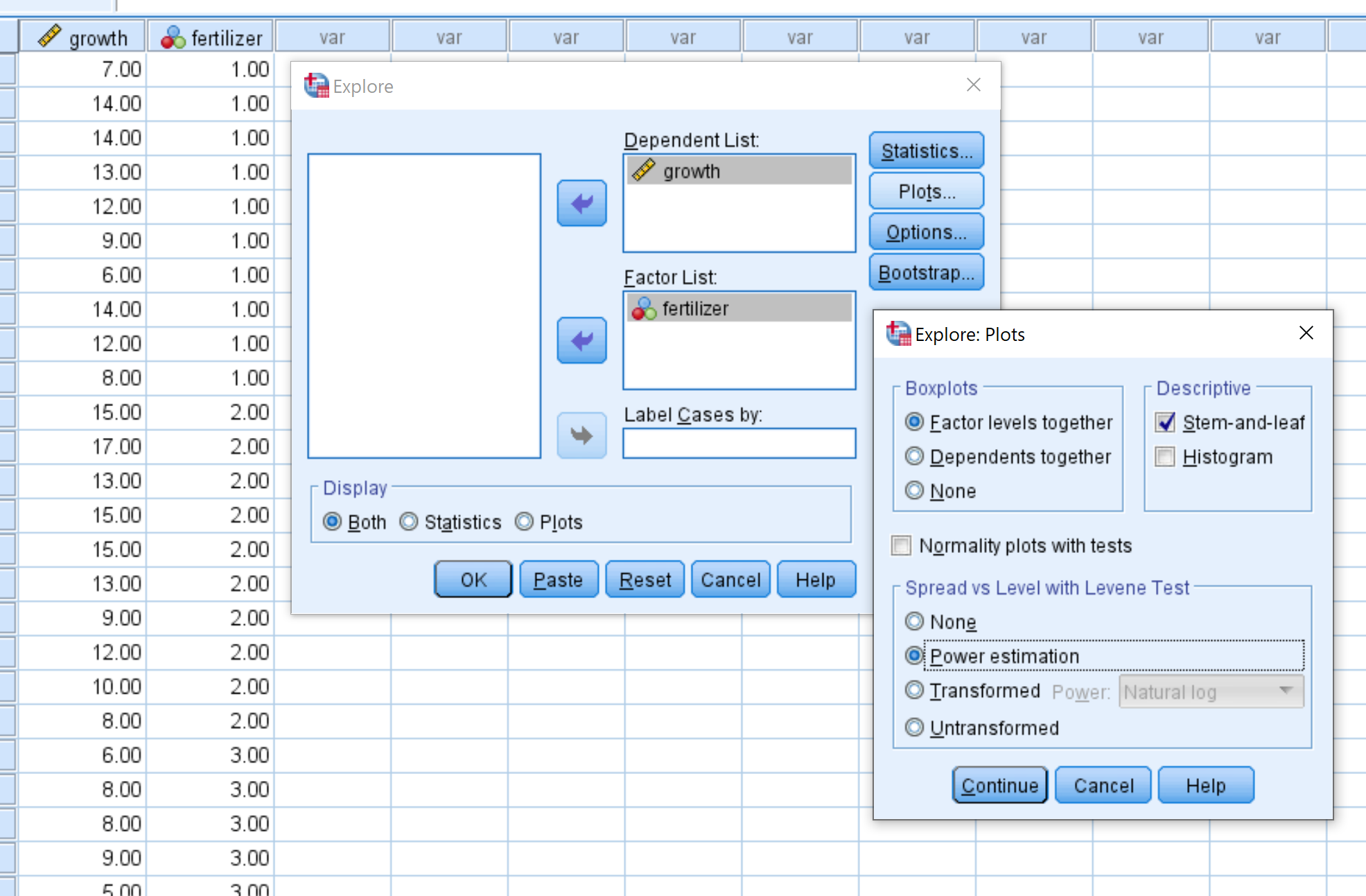
चरण 2: परीक्षण करने के लिए आवश्यक मान भरें।

विकास को आश्रित सूची के अंतर्गत बॉक्स में खींचें और उर्वरक खींचें   कारकों की सूची के अंतर्गत बॉक्स में।

फिर प्लॉट्स पर क्लिक करें और सुनिश्चित करें कि पावर एस्टीमेशन चयनित है। फिर जारी रखें पर क्लिक करें. फिर ओके पर क्लिक करें.

चरण 3: परिणामों की व्याख्या करें।

एक बार जब आप ओके पर क्लिक करेंगे, तो लेवेने परीक्षा परिणाम प्रदर्शित होंगे:

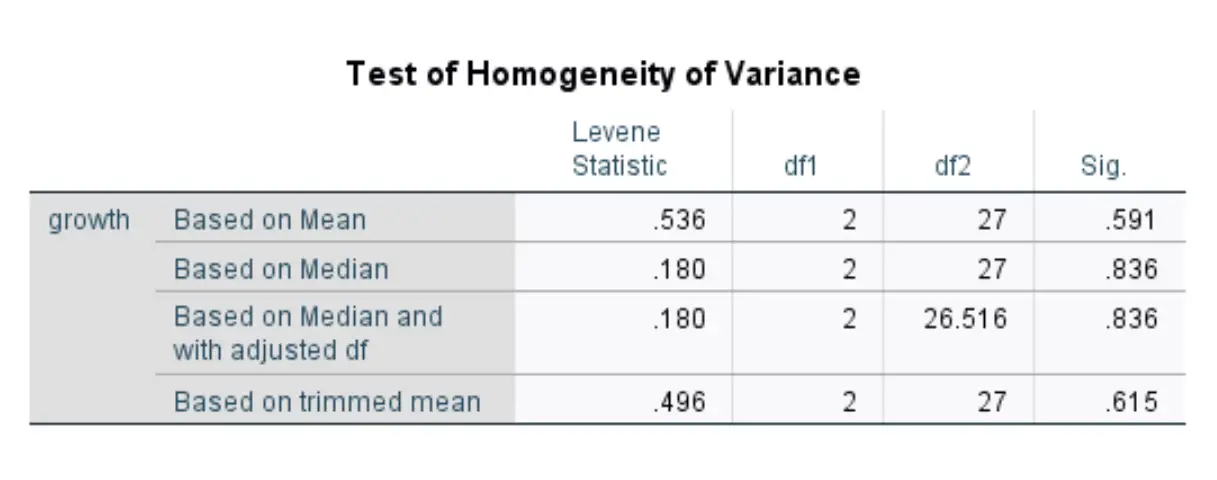
यह तालिका लेवेने परीक्षण के चार अलग-अलग संस्करणों के परीक्षण आँकड़े प्रदर्शित करती है। जिन संख्याओं में हमारी रुचि है वे पहली पंक्ति में हैं, जो माध्य के आधार पर लेवेने परीक्षण के परिणाम प्रदर्शित करती है।

परीक्षण आँकड़ा 0.536 है और संबंधित पी-मान 0.591* है।

चूँकि यह पी-मान 0.05 से कम नहीं है, हम शून्य परिकल्पना को अस्वीकार करने में विफल रहते हैं।

इसका मतलब यह है कि हमारे पास यह कहने के लिए पर्याप्त सबूत नहीं हैं कि तीनों उर्वरकों के बीच पौधों की वृद्धि में काफी अंतर है।

दूसरे शब्दों में, तीनों समूहों में समान भिन्नताएँ हैं। यदि हमें एक सांख्यिकीय परीक्षण ( एकतरफ़ा एनोवा की तरह) करना होता है जो मानता है कि प्रत्येक समूह में समान भिन्नता है, तो यह धारणा पूरी हो जाएगी।

* यह पी-मान अंश डीएफ = 2 और हर डीएफ = 27 के साथ 0.536 के एफ-सांख्यिकी से मेल खाता है। इस पी-मूल्य की गणना एफ वितरण कैलकुलेटर का उपयोग करके भी की जा सकती है।