वितरण समारोह

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 5, 2023 संभावना शून्य टिप्पणियां

इस लेख में आपको वितरण फ़ंक्शन का स्पष्टीकरण मिलेगा, इसके मूल्यों की गणना कैसे की जाती है और वितरण फ़ंक्शन का वास्तविक दुनिया का उदाहरण मिलेगा। इसके अतिरिक्त, आप वितरण फ़ंक्शन और घनत्व फ़ंक्शन के बीच अंतर देख पाएंगे।

वितरण कार्य क्या है?

वितरण फ़ंक्शन , जिसे संचयी वितरण फ़ंक्शन भी कहा जाता है, एक गणितीय फ़ंक्शन है जो वितरण की संचयी संभावना को इंगित करता है। अर्थात्, किसी भी मान के लिए वितरण फ़ंक्शन की छवि इस संभावना के बराबर होती है कि चर उस मान या उससे कम मान लेता है।

संचयी वितरण फ़ंक्शन को संक्षिप्त नाम एफडीए द्वारा भी संदर्भित किया जा सकता है, हालांकि इसका सामान्य प्रतीक पूंजी एफ है।

इसलिए वितरण फ़ंक्शन को निम्नलिखित सूत्र द्वारा परिभाषित किया गया है:

$F(x)=P[X\leq x]$

वितरण फलन की गणना कैसे करें

फिर हम बताते हैं कि संभाव्यता वितरण असतत है या निरंतर, इसके आधार पर वितरण फ़ंक्शन के मूल्य की गणना कैसे करें।

विवेकशील बक्सा

यदि यादृच्छिक चर असतत है, तो संचयी वितरण फ़ंक्शन x के बराबर या उससे कम सभी मानों की संभावनाओं के योग के बराबर है।

$\displaystyle F(x)=P[X\leq x]=\sum_{u\leq x}f(u)$

सोना

$f(u)$

असतत चर से जुड़ा संभाव्यता फ़ंक्शन है।

मामला जारी

यदि यादृच्छिक चर निरंतर है, तो संचयी वितरण फ़ंक्शन माइनस इनफिनिटी से प्रश्न में मूल्य तक घनत्व फ़ंक्शन के अभिन्न अंग के बराबर है।

$\displaystyle F(x)=P[X\leq x]=\int_{-\infty}^{x}f(u)du$

सोना

$f(u)$

सतत चर से संबद्ध घनत्व फलन है।

वितरण फलन उदाहरण

अब जब हम वितरण फ़ंक्शन की परिभाषा जानते हैं, तो आइए वितरण फ़ंक्शन मान की गणना करने का तरीका जानने के लिए एक व्यावहारिक चरण-दर-चरण उदाहरण देखें।

एक सिक्के को चार बार उछालने के यादृच्छिक प्रयोग के लिए वितरण फ़ंक्शन की गणना करें।

अभ्यास को हल करने के लिए, आपको पहले चार सिक्का उछाल के दौरान प्राप्त हेड की संख्या से जुड़ी सभी संभावनाओं की गणना करनी होगी:

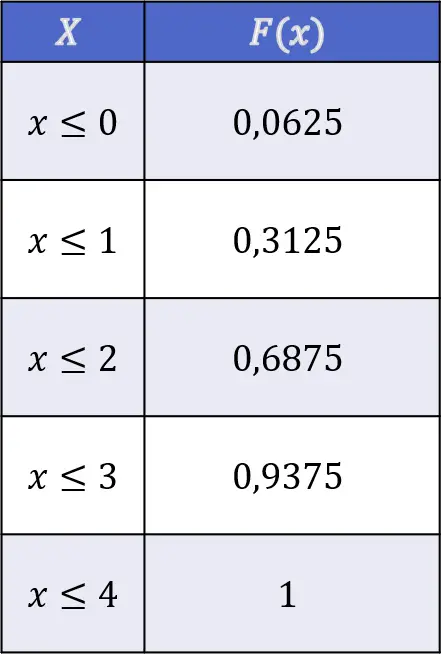
इस प्रकार, चूंकि यह एक अलग चर है, वितरण फ़ंक्शन की छवियों को निर्धारित करने के लिए प्रश्न में चर के मूल्य तक संभावनाओं को जोड़ना पर्याप्त है:

$\begin{array}{l}F(X\leq 0)=f(0)=0,0625\\[4ex]\begin{aligned}F(X\leq 1)& =f(0)+f(1)\\[1.1ex] & =0,0625+0,25=0,3125\end{aligned}\\[6ex]\begin{aligned}F(X\leq 2)& =f(0)+f(1)+f(2)\\[1.1ex] & =0,0625+0,25+0,375=0,6875\end{aligned}\\[6ex]\begin{aligned}F(X\leq 3)& =f(0)+f(1)+f(2)+f(3)\\[1.1ex] & =0,0625+0,25+0,375+0,25=0,9375\end{aligned}\\[6ex]\begin{aligned}F(X\leq 4)& =f(0)+f(1)+f(2)+f(3)+f(4)\\[1.1ex] & =0,0625+0,25+0,375+0,25+0,0625=1\end{aligned}\end{array}$

इस प्रकार, चार स्वतंत्र सिक्कों को उछालकर सिर उछालने के वितरण फलन के मान इस प्रकार हैं:

वितरण फलन के गुण

चर के प्रकार के बावजूद, वितरण फ़ंक्शन में हमेशा निम्नलिखित गुण होते हैं:

संचयी वितरण फ़ंक्शन का मान 0 और 1 समावेशी के बीच है।

$0\leq F(x) \leq 1$

जैसे ही x अनंत की ओर बढ़ता है, वितरण फलन की सीमा 1 के बराबर होती है।

$\displaystyle\lim_{x\to +\infty} F(x)=1$

दूसरी ओर, जब x शून्य से अनंत तक पहुंचता है तो वितरण फलन की सीमा शून्य होती है।

$\displaystyle\lim_{x\to -\infty} F(x)=0$

अपनी विशेषताओं के अनुसार, वितरण फलन एकरस और गैर-घटता हुआ है।

$x_1 \leq x_2 \implies F(x_1)\leq F(x_2)$

इसके अलावा, यदि
$a\leq b$

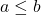
निम्नलिखित समीकरण संतुष्ट हैं.

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a )=1-F(a^-)\\[2ex]P(a<ul><li> Finally, if the statistical variable is continuous, the following equality is satisfied: </li></ul>[latex ]\begin{array}{l}P(a \le X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... the statistical variable is continuous, the
Please use \mathaccent for accents in math mode.
leading text: ...iable statistic is continuous, equality
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}

वितरण फलन और घनत्व फलन

अंत में, हम देखेंगे कि वितरण फ़ंक्शन और घनत्व फ़ंक्शन के बीच क्या अंतर है, क्योंकि ये दो सांख्यिकीय धारणाएं अक्सर भ्रमित होती हैं।

वितरण फलन और घनत्व फलन के बीच का अंतर संभाव्यता के प्रकार का है जिसे वे परिभाषित करते हैं। घनत्व फ़ंक्शन इस संभावना का वर्णन करता है कि चर एक निश्चित मान लेता है, जबकि वितरण फ़ंक्शन चर की संचयी संभावना का वर्णन करता है।

अर्थात्, वितरण फ़ंक्शन का उपयोग इस संभावना की गणना करने के लिए किया जाता है कि चर एक निश्चित मान के बराबर या उससे कम है।

ध्यान दें कि घनत्व फ़ंक्शन केवल निरंतर चर को संदर्भित करता है, इसलिए यह अंतर केवल तभी समझ में आता है जब अध्ययन किया जा रहा चर निरंतर हो।

ध्यान दें कि 1 के माध्य और 0.5 के मानक विचलन के साथ सामान्य वितरण का अनुसरण करने वाले एक चर के घनत्व फ़ंक्शन की तुलना में वितरण फ़ंक्शन का ग्राफिकल प्रतिनिधित्व कैसे बदलता है:

घनत्व फ़ंक्शन के बारे में अधिक जानने के लिए, निम्नलिखित लेख देखें:

➤ देखें: घनत्व फ़ंक्शन

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने