संचयी आवृत्ति बहुभुज

यह आलेख बताता है कि संचयी आवृत्ति बहुभुज क्या हैं। इस प्रकार, आपको संचयी आवृत्ति बहुभुज की परिभाषा मिलेगी, संचयी आवृत्ति बहुभुज का निर्माण कैसे करें और इस प्रकार के सांख्यिकीय ग्राफ की विशेषताएं क्या हैं।

स्पष्टीकरण शुरू करने से पहले, यह बेहतर ढंग से समझने के लिए कि संचयी आवृत्ति बहुभुज में क्या होता है और इसका निर्माण कैसे किया जाता है, निम्नलिखित पोस्ट पर जाने की अनुशंसा की जाती है:

संचयी आवृत्ति बहुभुज क्या है?

संचयी आवृत्ति बहुभुज एक प्रकार का सांख्यिकीय ग्राफ है जिसमें डेटा सेट की संचयी आवृत्तियों को बिंदुओं द्वारा दर्शाया जाता है और रेखाओं द्वारा जोड़ा जाता है। दूसरे शब्दों में, एक संचयी आवृत्ति बहुभुज एक सांख्यिकीय नमूने की संचयी आवृत्तियों का ग्राफिकल प्रतिनिधित्व है।

इसलिए, संचयी आवृत्ति बहुभुज का उपयोग एक निश्चित मान से नीचे डेटा की संख्या निर्धारित करने के लिए किया जाता है।

तार्किक रूप से, संचयी आवृत्ति बहुभुज की अवधारणा को समझने के लिए, आपको आंकड़ों में संचयी आवृत्ति के अर्थ के बारे में स्पष्ट होना चाहिए, इसलिए स्पष्टीकरण जारी रखने से पहले निम्नलिखित लेख की जांच करने की अनुशंसा की जाती है:

संचयी आवृत्ति बहुभुज कैसे बनाएं

संचयी आवृत्ति बहुभुज का प्रतिनिधित्व करने के लिए, निम्नलिखित चरणों का पालन किया जाना चाहिए:

1. वह सांख्यिकीय डेटा एकत्र करें जिससे आप संचित आवृत्ति बहुभुज का प्रतिनिधित्व करना चाहते हैं।
2. सबसे छोटे से सबसे बड़े तक क्रमबद्ध मानों के साथ एक आवृत्ति तालिका बनाएं।
3. डेटासेट की संचयी आवृत्तियों की गणना करें।
4. संचयी आवृत्तियों को ग्राफ़ पर बिंदुओं के रूप में आलेखित करें।
5. संचयी आवृत्ति बहुभुज बनाने के लिए ग्राफ़ पर लगातार बिंदुओं को एक रेखा से जोड़ें।

संचयी आवृत्ति बहुभुज का उदाहरण

ताकि आप देख सकें कि संचयी आवृत्ति बहुभुज कैसे बनाया जाता है, यहां एक ठोस उदाहरण दिया गया है:

• 50 लोगों का नमूना आकार मापा गया और डेटा को निम्नलिखित आवृत्ति तालिका में दर्ज किया गया। संचयी आवृत्ति बहुभुज का उपयोग करके डेटा को ग्राफ़ करें।

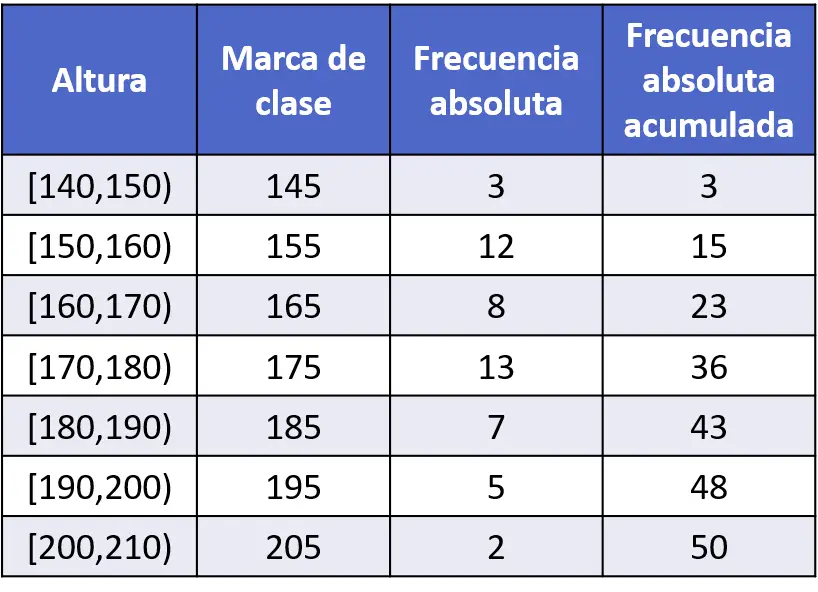
इस मामले में, संचित निरपेक्ष आवृत्तियों की गणना पहले ही की जा चुकी है, लेकिन यदि आप नहीं जानते कि यह कैसे करना है, तो आप निम्नलिखित लिंक पर क्लिक करके स्पष्टीकरण देख सकते हैं:

और एक बार जब संचयी निरपेक्ष आवृत्तियाँ ज्ञात हो जाती हैं, तो संचयी आवृत्तियों के बहुभुज का प्रतिनिधित्व करने के लिए एक ग्राफ पर बिंदुओं के रूप में मानों का प्रतिनिधित्व करना और फिर उन्हें एक सतत रेखा के साथ जोड़ना पर्याप्त होता है:

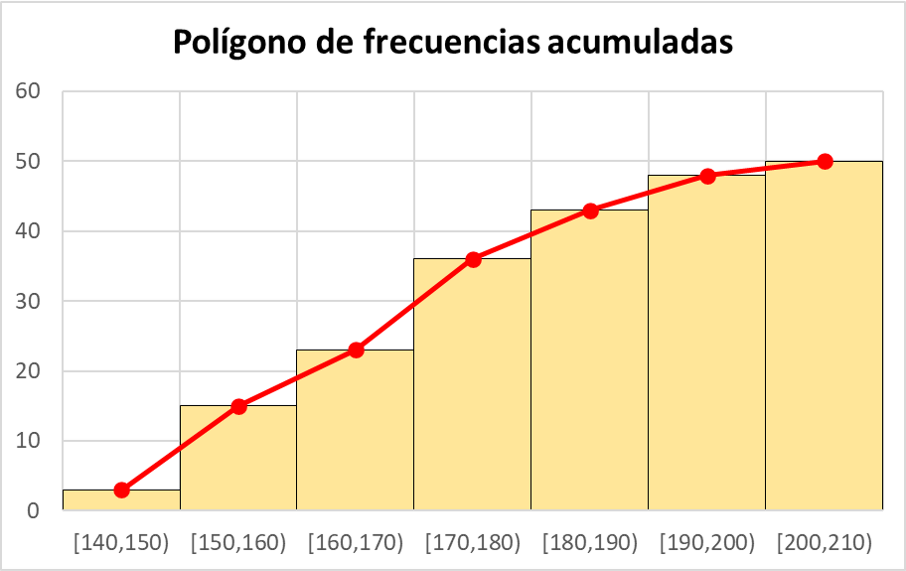
ध्यान दें कि एक संचयी आवृत्ति बहुभुज को संचयी आवृत्ति हिस्टोग्राम की पट्टियों के मध्य बिंदुओं को जोड़कर भी प्राप्त किया जा सकता है।

संचयी आवृत्ति बहुभुज के लक्षण

संचयी आवृत्ति बहुभुज की विशेषताएँ इस प्रकार हैं:

• यदि संचित निरपेक्ष आवृत्तियों को संचयी आवृत्ति बहुभुज में दर्शाया जाता है, तो अंतिम बिंदु हमेशा डेटा की कुल संख्या होगी।
• लेकिन यदि संचयी सापेक्ष आवृत्तियों को ग्राफ़ पर प्लॉट किया जाता है, तो अंतिम बिंदु हमेशा 1 होगा।
• संचयी आवृत्ति बहुभुज में केवल मात्रात्मक चर का प्रतिनिधित्व किया जा सकता है; इस प्रकार का सांख्यिकीय आरेख गुणात्मक चर के लिए उपयोगी नहीं है।
• संचयी आवृत्ति बहुभुज आपको दृश्य रूप से यह जानने देता है कि कितने डेटा बिंदु एक निश्चित मान से नीचे हैं।