समूहीकृत डेटा

यह आलेख बताता है कि समूहीकृत डेटा क्या है और डेटा को कैसे समूहीकृत किया जाता है। इसके अतिरिक्त, आपको एक हल किया गया अभ्यास मिलेगा जिसमें डेटा को अंतराल के आधार पर समूहीकृत किया गया है।

समूहीकृत डेटा क्या है?

आंकड़ों में, बिन्ड डेटा अंतरालों में समूहीकृत डेटा है। दूसरे शब्दों में, समूहीकृत डेटा नियमित अंतराल पर एकत्र किया गया डेटा है ताकि उनका एक साथ अध्ययन किया जा सके।

इसलिए, सांख्यिकीय डेटा के एक सेट को समूहीकृत करते समय, इसे अलग-अलग अंतरालों में विभाजित किया जाता है, ताकि डेटा का प्रत्येक टुकड़ा केवल एक अंतराल से संबंधित हो सके।

संक्षेप में, आंकड़ों में, डेटा क्लस्टरिंग कई डेटा को संयुक्त रूप से विश्लेषण करने की अनुमति देती है, ताकि एक अंतराल के भीतर समूहीकृत डेटा को डेटा के एक टुकड़े के रूप में माना जाए। इसके अतिरिक्त, जब नमूना बहुत बड़ा हो तो डेटा पूलिंग बहुत उपयोगी होती है।

समूहीकृत डेटा का उदाहरण

समूहीकृत डेटा की परिभाषा को देखते हुए, नीचे एक ठोस उदाहरण दिया गया है कि कैसे डेटा के एक सेट को विभिन्न अंतरालों में समूहीकृत किया जाता है।

• 50 अलग-अलग लोगों का नमूना आकार मापा गया और सभी मान निम्नलिखित डेटा तालिका में दर्ज किए गए। डेटा सेट को अंतरालों में समूहित करें, फिर डेटा को ग्राफ़ करें।

सबसे पहले, हमें डेटा को अंतरालों में अलग करना होगा। इसके लिए कई विधियाँ हैं, लेकिन स्टर्गेस का नियम सबसे अधिक उपयोग किया जाता है, क्योंकि यह आपको अंतरालों की आदर्श संख्या की गणना करने की अनुमति देता है:

इसलिए हमें डेटा को सात अलग-अलग अंतरालों में अलग करने की आवश्यकता है। अब हमें यह जानने की जरूरत है कि प्रत्येक अंतराल में कितनी चौड़ाई होनी चाहिए। ऐसा करने के लिए, बस अधिकतम मान घटाकर न्यूनतम मान को अंतरालों की कुल संख्या से विभाजित करें:

संक्षेप में, आयाम 9 के 7 अंतराल होने चाहिए, इसलिए स्टर्गेस नियम के अनुसार गणना किए गए अंतराल इस प्रकार हैं:

और एक बार जब हम अंतरालों की गणना कर लेते हैं, तो हम प्रत्येक अंतराल में डेटा के एक टुकड़े के प्रकट होने की संख्या की गणना करते हैं और हम समूहीकृत डेटा के साथ एक तालिका बनाते हैं:

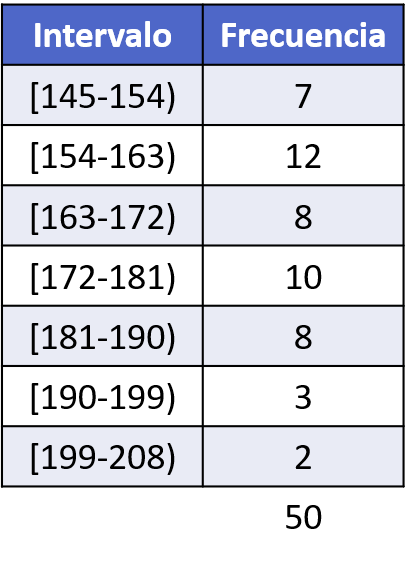
ध्यान रखें कि समूहीकृत डेटा (सापेक्ष आवृत्ति, संचयी आवृत्ति, आदि) से और भी अधिक आवृत्ति प्रकारों की गणना की जा सकती है। समूहीकृत डेटा के साथ संपूर्ण आवृत्ति तालिका बनाने का तरीका देखने के लिए, यहां क्लिक करें:

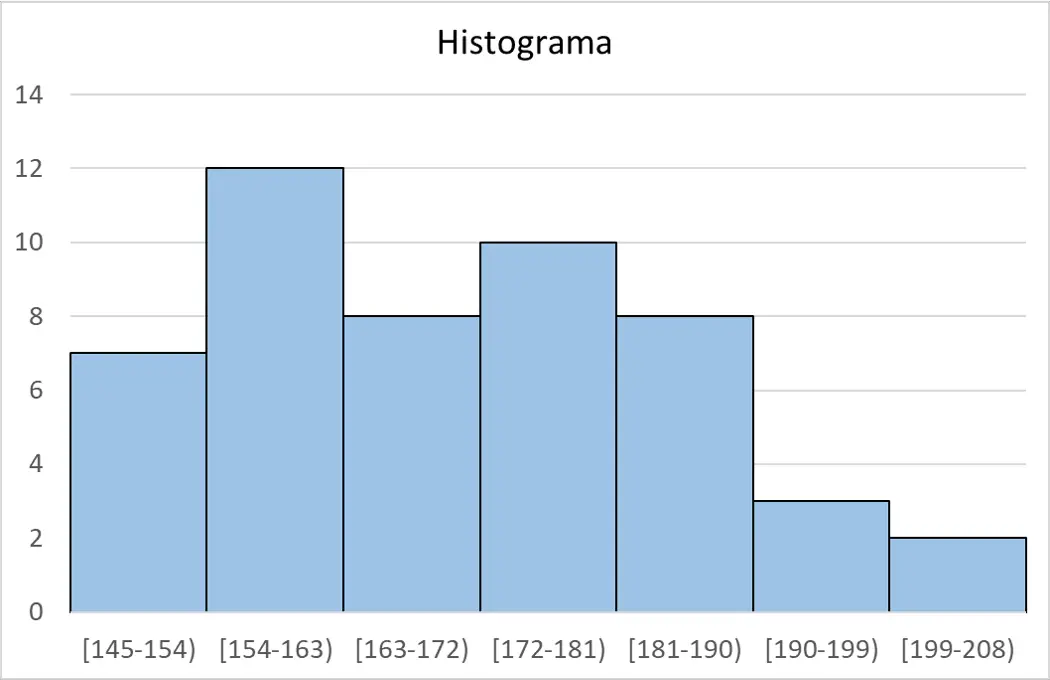
अंत में, प्रत्येक अंतराल की आवृत्ति वाली तालिका से, हम हिस्टोग्राम में समूहीकृत डेटा को ग्राफ़ कर सकते हैं।

समूहीकृत और असमूहीकृत डेटा

असमूहीकृत डेटा वह डेटा है जिसे अंतरालों में विभाजित नहीं किया जाता है, बल्कि प्रत्येक मान का अलग से अध्ययन किया जाता है।

ऊपर दिए गए उदाहरण का अनुसरण करते हुए, यदि हमने डेटा को समूहीकृत नहीं किया होता, तो हमें प्रत्येक मान की आवृत्ति ज्ञात करनी होती। अर्थात् हमें 158, 165, 174 आदि का मान कितनी बार ज्ञात करना चाहिए। दोहराया जाता है. हालाँकि, इस मामले में डेटा को अंतराल के आधार पर समूहित करना बेहतर था क्योंकि हमारे पास बड़ी मात्रा में डेटा था और इसके अलावा, कई मान समान थे।

इसलिए, एक सांख्यिकीय अध्ययन के दौरान, गणना करने से पहले, यह तय करना महत्वपूर्ण है कि डेटा को अंतराल के आधार पर समूहीकृत किया जाना चाहिए या नहीं, क्योंकि यह बाकी जांच की स्थिति तय करेगा।

डेटा को कब समेकित किया जाना चाहिए?

सामान्य तौर पर, जब चर निरंतर हो तो डेटा को अंतरालों में समूहीकृत किया जाना चाहिए। यदि चर निरंतर है, तो हमारे पास आम तौर पर कई मान होते हैं और वे एक-दूसरे के बहुत करीब होते हैं, इसलिए अध्ययन को सरल बनाने के लिए उन्हें अंतराल में समूहीकृत किया जा सकता है।

तार्किक रूप से, भले ही चर निरंतर न हो, अगर हमारे पास बहुत सारा डेटा है, तो इसे अंतरालों में भी समूहीकृत किया जा सकता है, जिससे सांख्यिकीय विश्लेषण आसान हो जाता है। लेकिन आम तौर पर डेटा को समूहीकृत करने का मानदंड चर का प्रकार होता है: यदि चर निरंतर है, तो डेटा को आम तौर पर अंतराल में अलग किया जाता है।