समूहीकृत डेटा का माध्यिका कैसे ज्ञात करें: उदाहरणों के साथ

हम अक्सर किसी तरह से एक साथ समूहीकृत किए गए डेटा के माध्य की गणना करना चाहते हैं।

याद रखें कि माध्यिका उस मान का प्रतिनिधित्व करती है जो सीधे डेटा सेट के मध्य में स्थित होता है, जब सभी मानों को सबसे छोटे से सबसे बड़े तक क्रमबद्ध किया जाता है।

उदाहरण के लिए, मान लें कि हमारे पास निम्नलिखित समूहीकृत डेटा है:

यद्यपि सटीक माध्यिका की गणना करना संभव नहीं है क्योंकि हम कच्चे डेटा मानों को नहीं जानते हैं, निम्नलिखित सूत्र का उपयोग करके माध्यिका का अनुमान लगाना संभव है:

समूहीकृत डेटा का माध्य = L + W[(N/2 – C) / F]

सोना:

• एल : माध्यिका वर्ग की निचली सीमा
• डब्ल्यू : माध्यिका वर्ग चौड़ाई
• एन : कुल आवृत्ति
• सी : माध्यिका वर्ग तक संचयी आवृत्ति
• एफ : माध्यिका वर्ग आवृत्ति

नोट : मध्यम वर्ग वह वर्ग है जिसमें N/2 पर स्थित मान होता है। उपरोक्त उदाहरण में, N = 23 कुल मान हैं। इस प्रकार, स्थिति 23/2 = 11.5 में माध्य मान है, जो 21-30 वर्ग में होगा।

निम्नलिखित उदाहरण दिखाते हैं कि विभिन्न परिदृश्यों में समूहीकृत डेटा के माध्य की गणना कैसे करें।

उदाहरण 1: समूहीकृत डेटा के माध्यिका की गणना करें

मान लीजिए कि हमारे पास निम्नलिखित आवृत्ति वितरण है जो एक निश्चित कक्षा में 40 छात्रों द्वारा ग्रेड की गई परीक्षा को दर्शाता है:

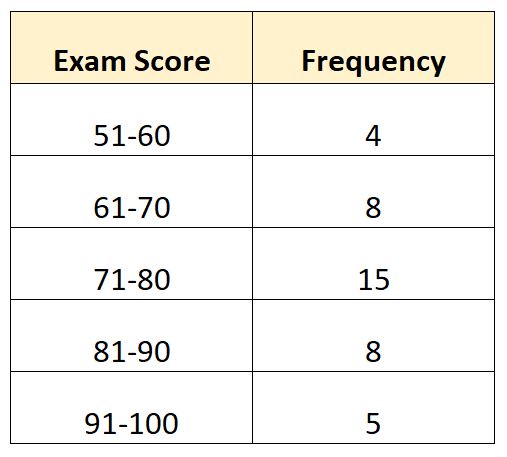
इस उदाहरण में, N = 40 कुल मान हैं। तो माध्यिका मान उस वर्ग में है जहां 40/2 = 20 स्थित है। 20वां सबसे बड़ा मान वर्ग 71-80 में होगा।

यह जानकर, हम निम्नलिखित मानों की गणना कर सकते हैं:

• एल : निम्न मध्यम वर्ग सीमा: 71
• डब्ल्यू : माध्यिका वर्ग चौड़ाई: 9
• एन : कुल आवृत्ति: 40
• सी : माध्यिका वर्ग तक संचयी आवृत्ति: 12
• एफ : माध्यिका वर्ग आवृत्ति: 15

वितरण के माध्यिका की गणना के लिए हम इन मानों को सूत्र में प्लग कर सकते हैं:

• माध्यिका = L + W[(N/2 – C) / F]
• माध्यिका = 71 + 9[(40/2 – 12)/15]
• माध्यिका = 75.8

हमारा अनुमान है कि औसत परीक्षा स्कोर 75.8 होगा।

उदाहरण 2: समूहीकृत डेटा के माध्यिका की गणना करें

मान लीजिए कि हमारे पास निम्नलिखित आवृत्ति वितरण है जो 60 बास्केटबॉल खिलाड़ियों द्वारा प्रति गेम बनाए गए अंकों की संख्या दर्शाता है:

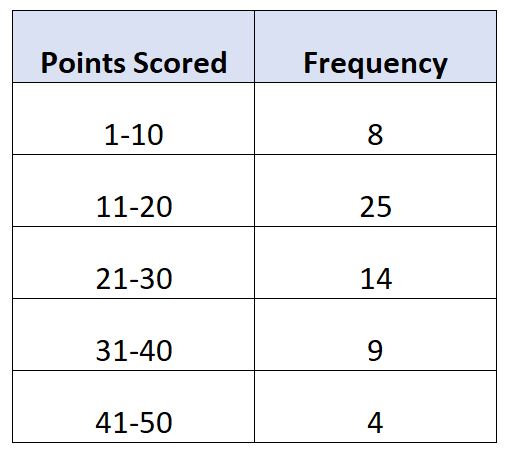
इस उदाहरण में, N = 60 कुल मान हैं। इस प्रकार, माध्यिका मान उस वर्ग में है जहां 60/2 = 30 स्थित है। 30वां सबसे बड़ा मान कक्षा 11-20 में होगा।

यह जानकर, हम निम्नलिखित मानों की गणना कर सकते हैं:

• एल : निम्न मध्यम वर्ग सीमा: 11
• डब्ल्यू : माध्यिका वर्ग चौड़ाई: 9
• एन : कुल आवृत्ति: 60
• सी : माध्यिका वर्ग तक संचयी आवृत्ति: 8
• एफ : माध्यिका वर्ग आवृत्ति: 25

वितरण के माध्यिका की गणना के लिए हम इन मानों को सूत्र में प्लग कर सकते हैं:

• माध्यिका = L + W[(N/2 – C) / F]
• माध्यिका = 11 + 9[(60/2 – 8)/25]
• माध्यिका = 18.92

हमारा अनुमान है कि औसत परीक्षा स्कोर 18.92 होगा।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि समूहीकृत डेटा के साथ अन्य सामान्य ऑपरेशन कैसे करें:

समूहीकृत डेटा का माध्य और मानक विचलन कैसे ज्ञात करें
समूहीकृत डेटा मोड कैसे खोजें
समूहीकृत डेटा के लिए प्रतिशतक रैंकिंग की गणना कैसे करें