एनोवा में समूह के भीतर या समूह के बीच भिन्नता

एक-तरफ़ा एनोवा का उपयोग यह निर्धारित करने के लिए किया जाता है कि तीन या अधिक स्वतंत्र समूहों के साधन बराबर हैं या नहीं।

एक-तरफ़ा एनोवा निम्नलिखित शून्य और वैकल्पिक परिकल्पनाओं का उपयोग करता है:

• एच ₀ : सभी समूह साधन समान हैं।
• एच _ए : कम से कम एक समूह का औसत दूसरों से अलग है।

हर बार जब आप एक-तरफ़ा एनोवा निष्पादित करते हैं, तो आपके पास एक सारांश तालिका होगी जो निम्नलिखित की तरह दिखती है:

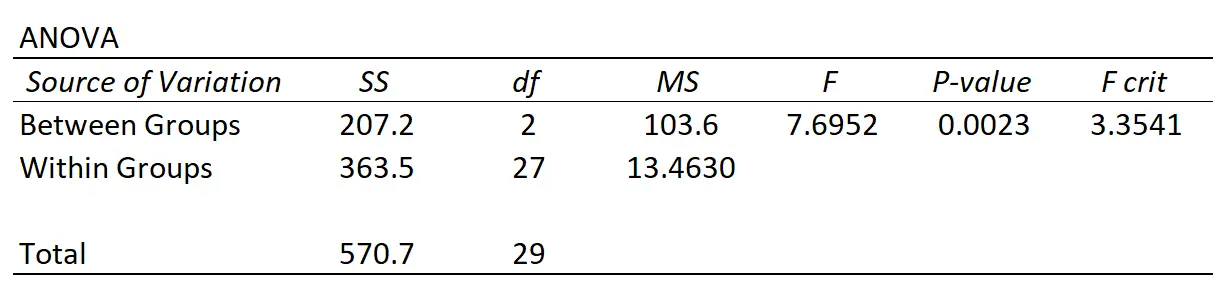
हम देख सकते हैं कि भिन्नता के दो अलग-अलग स्रोत हैं जिन्हें एनोवा मापता है:

समूहों के बीच भिन्नता : प्रत्येक समूह के औसत और समग्र औसत के बीच कुल भिन्नता।

समूह के भीतर भिन्नता : प्रत्येक समूह में व्यक्तिगत मूल्यों और उनके समूह औसत की कुल भिन्नता।

यदि समूहों के बीच भिन्नता समूह के भीतर भिन्नता के सापेक्ष अधिक है, तो एनोवा का एफ आँकड़ा अधिक होगा और संबंधित पी-मूल्य कम होगा, जिससे यह अधिक संभावना है कि शून्य परिकल्पना खारिज कर दी जाएगी जिसके अनुसार समूह के साधन बराबर हैं।

निम्नलिखित उदाहरण दिखाता है कि व्यवहार में एक-तरफ़ा एनोवा के लिए समूह के बीच भिन्नता और समूह के भीतर भिन्नता की गणना कैसे करें।

उदाहरण: एनोवा में एक समूह के भीतर और समूहों के बीच भिन्नता की गणना करना

मान लीजिए कि हम यह निर्धारित करना चाहते हैं कि क्या तीन अलग-अलग अध्ययन विधियों से अलग-अलग औसत परीक्षा अंक प्राप्त होते हैं। इसका परीक्षण करने के लिए, हम 30 छात्रों को भर्ती करते हैं और यादृच्छिक रूप से 10 प्रत्येक को एक अलग अध्ययन पद्धति का उपयोग करने के लिए नियुक्त करते हैं ।

प्रत्येक समूह में छात्रों के परीक्षा परिणाम नीचे दिखाए गए हैं:

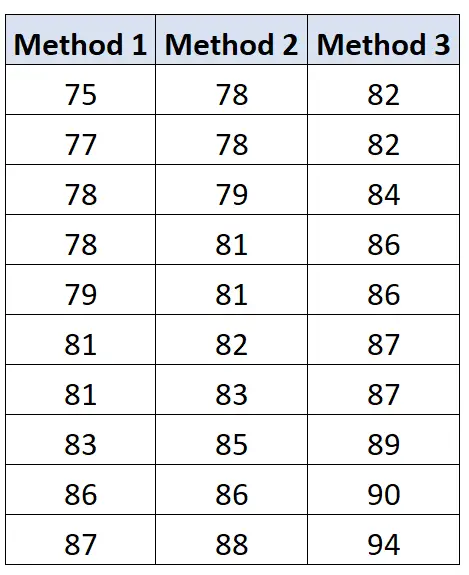
समूहों के बीच भिन्नता की गणना के लिए हम निम्नलिखित सूत्र का उपयोग कर सकते हैं:

समूहों के बीच भिन्नता = Σn _j (X _j – X ..) ²

सोना:

• n _j : समूह j का नमूना आकार
• Σ : एक प्रतीक जिसका अर्थ है “योग”
• X _j : समूह j का औसत
• एक्स .. : समग्र औसत

इस मान की गणना करने के लिए, हम पहले प्रत्येक समूह के औसत और समग्र औसत की गणना करेंगे:

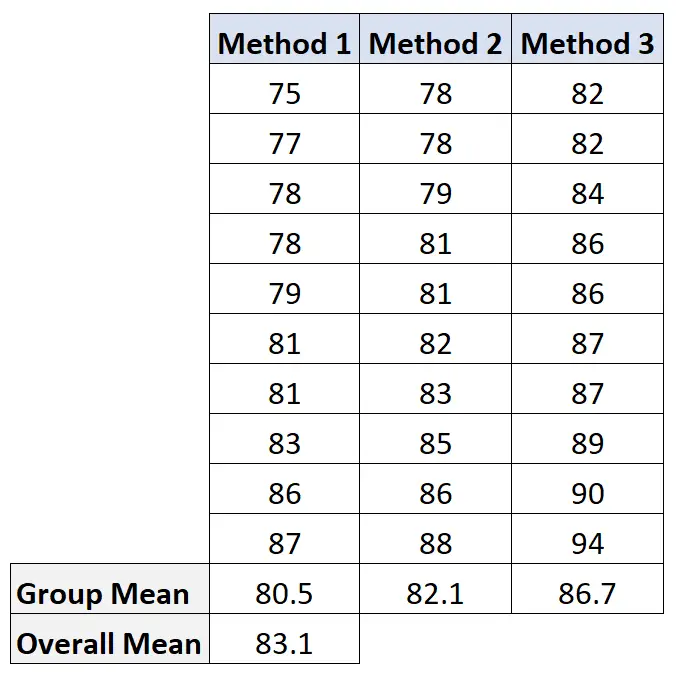
फिर हम समूहों के बीच भिन्नता की गणना इस प्रकार करते हैं: 10(80.5-83.1) ² + 10(82.1-83.1) ² + 10(86.7-83.1) ² = 207.2 ।

फिर हम समूह के भीतर भिन्नता की गणना करने के लिए निम्नलिखित सूत्र का उपयोग कर सकते हैं:

अंतर-समूह भिन्नता : Σ(X _ij – X _j ) ²

सोना:

• Σ : एक प्रतीक जिसका अर्थ है “योग”
• X _ij : समूह j का ^ith अवलोकन
• X _j : समूह j का औसत

हमारे उदाहरण में, हम समूह के भीतर भिन्नता की गणना इस प्रकार करते हैं:

समूह 1: (75-80.5) ² + (77-80.5) ² +   (78-80.5) ²⁺   (78-80.5) ²⁺   (79-80.5) ²⁺   (81-80.5) ²⁺   (81-80.5) ²⁺   (83-80.5) ²⁺   (86-80.5) ²⁺   (87-80.5) ² = 136.5

समूह 2: (78-82.1) ² + (78-82.1) ² +   (79-82.1) ²⁺   (81-82.1) ²⁺   (81-82.1) ²⁺   (82-82.1) ²⁺   (83-82.1) ²⁺   (85-82.1) ²⁺   (86-82.1) ²⁺   (88-82.1) ² = 104.9

समूह 3: (82-86.7) ² + (82-86.7) ² +   (84-86.7) ²⁺   (86-86.7) ²⁺   (86-86.7) ²⁺   (87-86.7) ²⁺   (87-86.7) ²⁺   (89-86.7) ²⁺   (90-86.7) ²⁺   (94-86.7) ² = 122.1

समूह के भीतर भिन्नता: 136.5 + 104.9 + 122.1 = 363.5

यदि हम इस डेटासेट का उपयोग करके एक-तरफ़ा एनोवा करने के लिए सांख्यिकीय सॉफ़्टवेयर का उपयोग करते हैं, तो हमें निम्नलिखित एनोवा तालिका मिलेगी:

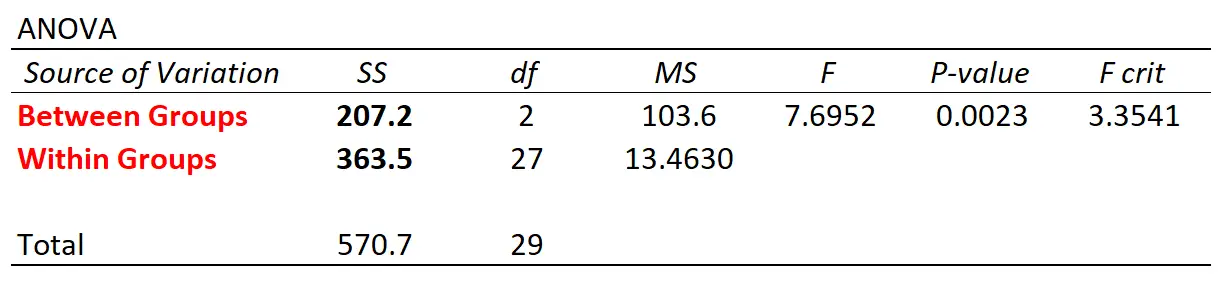
ध्यान दें कि समूह के बीच और समूह के भीतर भिन्नता मान उन मूल्यों से मेल खाते हैं जिनकी हमने मैन्युअल रूप से गणना की थी।

तालिका में समग्र एफ आँकड़ा समूहों के बीच भिन्नता और समूह के भीतर भिन्नता के बीच संबंध को मापने का एक तरीका है।

एफ आँकड़ा जितना बड़ा होगा, समूहों के बीच भिन्नता उतनी ही अधिक होगी अर्थात समूहों के भीतर भिन्नता के सापेक्ष।

तो, एफ आँकड़ा जितना बड़ा होगा, यह उतना ही अधिक स्पष्ट होगा कि समूह के साधनों के बीच अंतर है।

हम इस उदाहरण में देख सकते हैं कि पी-मान जो 7.6952 के एफ-सांख्यिकी से मेल खाता है वह .0023 है।

चूँकि यह मान α = 0.05 से कम है, हम एनोवा की शून्य परिकल्पना को अस्वीकार करते हैं और निष्कर्ष निकालते हैं कि तीन अध्ययन तकनीकों से परीक्षा में समान अंक नहीं मिलते हैं।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल एनोवा मॉडल के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

वन-वे एनोवा का परिचय
एनोवा में एफ मान और पी मान की व्याख्या कैसे करें
संपूर्ण गाइड: एनोवा परिणामों की रिपोर्ट कैसे करें