साधनों में अंतर के लिए परिकल्पना परीक्षण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि आंकड़ों में परिकल्पना परीक्षण के बीच क्या अंतर है और इसका उपयोग किस लिए किया जाता है। इसी तरह, आप जानेंगे कि साधनों में अंतर पर एक परिकल्पना परीक्षण कैसे किया जाता है और चरण-दर-चरण हल किया गया अभ्यास कैसे किया जाता है।

माध्य अंतर के लिए परिकल्पना परीक्षण क्या है?

साधनों में अंतर के लिए परिकल्पना परीक्षण एक सांख्यिकीय परीक्षण है जिसका उपयोग इस परिकल्पना को अस्वीकार करने या स्वीकार करने के लिए किया जाता है कि दो आबादी के साधन अलग-अलग हैं। अर्थात्, साधनों में अंतर परिकल्पना परीक्षण का उपयोग यह निर्धारित करने के लिए किया जाता है कि दो जनसंख्या के साधन समान हैं या भिन्न हैं।

ध्यान रखें कि परिकल्पना परीक्षण में लिए गए निर्णय पहले से स्थापित आत्मविश्वास के स्तर पर आधारित होते हैं, इसलिए कोई यह गारंटी नहीं दे सकता कि परिकल्पना परीक्षण का परिणाम हमेशा सही होता है, बल्कि यह कि यह सबसे संभावित परिणाम है जो सत्य है।

दो साधनों के अंतर के लिए परिकल्पना परीक्षण में परीक्षण आंकड़ों की गणना करना और शून्य परिकल्पना को अस्वीकार करने या न करने के लिए महत्वपूर्ण मान से तुलना करना शामिल है। नीचे हम देखेंगे कि साधनों में अंतर के लिए परिकल्पना परीक्षण कैसे करें।

अंत में, याद रखें कि सांख्यिकी में, परिकल्पना परीक्षण को परिकल्पना विरोधाभास, परिकल्पना परीक्षण या महत्व परीक्षण भी कहा जा सकता है।

➤ देखें: साधनों में अंतर का नमूना वितरण

साधनों में अंतर के लिए परिकल्पना परीक्षण सूत्र

साधनों में अंतर के बारे में परिकल्पनाओं का परीक्षण करने के लिए जिस सूत्र का उपयोग किया जाना चाहिए, वह इस पर निर्भर करता है कि जनसंख्या भिन्नताएं ज्ञात हैं या नहीं और यदि नहीं, तो उन्हें समान या भिन्न माना जा सकता है या नहीं। इसलिए, इस अनुभाग में, हम देखेंगे कि मामले के आधार पर किस सूत्र का उपयोग करना है।

ज्ञात विविधताएँ

भिन्नता ज्ञात होने पर साधनों में अंतर के लिए परिकल्पना परीक्षण आँकड़ों की गणना करने का सूत्र इस प्रकार है:

$\displaystyle Z=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

सोना:

$Z$

ज्ञात भिन्नता वाले दो साधनों के अंतर के लिए परिकल्पना परीक्षण आँकड़ा है, जो एक मानक सामान्य वितरण का अनुसरण करता है।
$\mu_1$

जनसंख्या 1 का माध्य है.
$\mu_2$

जनसंख्या का माध्य है 2.
$\overline{x_1}$

नमूना 1 का माध्य है.
$\overline{x_2}$

नमूना 2 का माध्य है.
$\sigma_1$

जनसंख्या 1 का मानक विचलन है.
$\sigma_2$

जनसंख्या 2 का मानक विचलन है।
$n_1$

नमूना आकार 1 है.
$n_2$

नमूना आकार 2 है.

ध्यान रखें कि यह सबसे कम सामान्य मामला है, इसलिए इस सूत्र का उपयोग केवल कुछ विशिष्ट मामलों में ही किया जाता है।

अज्ञात और समान विचलन

जब जनसंख्या भिन्नताएं अज्ञात हैं लेकिन बराबर मानी जाती हैं तो साधनों में अंतर के लिए परिकल्पना परीक्षण आंकड़ों की गणना करने का सूत्र है :

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

सोना:

$t$

अज्ञात भिन्नताओं के साथ साधनों में अंतर के लिए परिकल्पना परीक्षण आँकड़ा है, जो स्वतंत्रता की n ₁ + n ₂ -2 डिग्री के साथ एक छात्र के t वितरण का अनुसरण करता है।
$\mu_1$

जनसंख्या 1 का माध्य है.
$\mu_2$

जनसंख्या का माध्य है 2.
$\overline{x_1}$

नमूना 1 का माध्य है.
$\overline{x_2}$

नमूना 2 का माध्य है.
$s_p$

संयुक्त मानक विचलन है.
$n_1$

नमूना आकार 1 है.
$n_2$

नमूना आकार 2 है.

दो नमूनों के संयुक्त मानक विचलन की गणना निम्न सूत्र से की जाती है:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

अज्ञात और विभिन्न विविधताएँ

जब जनसंख्या भिन्नताएं अज्ञात होती हैं और इसके अलावा, उन्हें अलग-अलग माना जाता है, तो साधनों में अंतर के लिए परिकल्पना परीक्षण आंकड़ों की गणना करने का सूत्र इस प्रकार है:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

सोना:

$t$

अज्ञात भिन्नताओं वाले साधनों में अंतर के लिए परिकल्पना परीक्षण आँकड़ा है, जो छात्र के टी वितरण का अनुसरण करता है।
$\mu_1$

जनसंख्या 1 का माध्य है.
$\mu_2$

जनसंख्या का माध्य है 2.
$\overline{x_1}$

नमूना 1 का माध्य है.
$\overline{x_2}$

नमूना 2 का माध्य है.
$\sigma_1$

जनसंख्या 1 का मानक विचलन है.
$\sigma_2$

जनसंख्या 2 का मानक विचलन है।
$n_1$

नमूना आकार 1 है.
$n_2$

नमूना आकार 2 है.

हालाँकि, इस मामले में, छात्र के टी वितरण की स्वतंत्रता की डिग्री की गणना निम्नलिखित सूत्र का उपयोग करके की जाती है:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ देखें: साधनों के अंतर के लिए कॉन्फिडेंस इंटरवल फॉर्मूला

साधनों में अंतर के लिए परिकल्पना परीक्षण का ठोस उदाहरण

साधनों में अंतर पर परिकल्पना परीक्षण की अवधारणा को आत्मसात करने के लिए, हम इस प्रकार की परिकल्पना परीक्षण का एक ठोस उदाहरण देखेंगे।

आप दो प्रतिस्पर्धी कंपनियों के वेतन पर एक सांख्यिकीय अध्ययन करना चाहते हैं, विशेष रूप से, आप यह निर्धारित करना चाहते हैं कि क्या दोनों कंपनियों का औसत वेतन अलग है। ऐसा करने के लिए, एक कंपनी के 47 श्रमिकों का एक नमूना लिया जाता है और दूसरी कंपनी के 55 श्रमिकों का एक और नमूना लिया जाता है। पहले नमूने से औसत वेतन $40,000 और $12,000 का मानक विचलन प्राप्त होता है, जबकि दूसरे नमूने से $46,000 का औसत वेतन और $18,000 का मानक विचलन प्राप्त होता है। यह निर्धारित करने के लिए कि औसत वेतन भिन्न हैं या नहीं, 5% महत्व स्तर के साथ एक परिकल्पना परीक्षण करें।

इस मामले में, दो साधनों के अंतर के लिए परिकल्पना परीक्षण की शून्य परिकल्पना और वैकल्पिक परिकल्पना इस प्रकार हैं:

$\begin{cases}H_0: \mu_1-\mu_2=0\\[2ex] H_1:\mu_1-\mu_2\neq 0 \end{cases}$

इस मामले में, जनसंख्या अंतर ज्ञात नहीं है, लेकिन यह माना जा सकता है कि वे बराबर हैं क्योंकि वे प्रतिस्पर्धी कंपनियां हैं और जिस बाजार में वे काम करते हैं वहां की कामकाजी स्थितियां बहुत समान हैं। इसलिए, साधनों में अंतर के लिए परिकल्पना परीक्षण आँकड़ों का सूत्र जिसका हमें उपयोग करना चाहिए वह है:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

इसलिए हम दो नमूनों के एकत्रित मानक विचलन की गणना करते हैं:

$\begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(47-1)\cdot 12000^2+(55-1)\cdot 18000^2}{47+55-2}}\\[2ex]s_p&=15530,61\end{aligned}$

अब हम साधनों में अंतर के लिए परिकल्पना परीक्षण सूत्र लागू करते हैं:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}=\cfrac{(40000-46000)-0}{\displaystyle 15530,61\sqrt{\frac{1}{47}+\frac{1}{55}}}=-1,94$

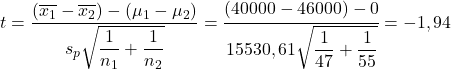
दूसरी ओर, हम छात्र की टी तालिका में माध्य में अंतर के लिए परिकल्पना परीक्षण के महत्वपूर्ण मूल्य की तलाश करते हैं:

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 100}=1,984\end{array}$

फिर, चूँकि परीक्षण आँकड़ों का निरपेक्ष मान महत्वपूर्ण परीक्षण मान से कम है, शून्य परिकल्पना स्वीकार कर ली जाती है और वैकल्पिक परिकल्पना अस्वीकार कर दी जाती है।

$|-1,94|=1,94<1,984 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने

माध्य अंतर के लिए परिकल्पना परीक्षण क्या है?

साधनों में अंतर के लिए परिकल्पना परीक्षण सूत्र

ज्ञात विविधताएँ

अज्ञात और समान विचलन

अज्ञात और विभिन्न विविधताएँ

साधनों में अंतर के लिए परिकल्पना परीक्षण का ठोस उदाहरण

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

एक टिप्पणी जोड़ने