मानक सामान्य वितरण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 4, 2023 संभावना शून्य टिप्पणियां

यह आलेख बताता है कि मानक सामान्य वितरण क्या है और इसका उपयोग किस लिए किया जाता है। आपको मानक सामान्य वितरण के गुण, उसके विशिष्ट मूल्यों वाली तालिका और इसके अलावा, एक हल किया गया अभ्यास भी मिलेगा।

मानक सामान्य वितरण क्या है?

मानक सामान्य वितरण , जिसे इकाई सामान्य वितरण भी कहा जाता है, सामान्य वितरण का सबसे सरल मामला है। अधिक सटीक रूप से, मानक सामान्य वितरण क्रमशः 0 और 1 के बराबर माध्य और मानक विचलन मान वाला एक सामान्य वितरण है।

इसलिए, मानक सामान्य वितरण को एन (0,1) के रूप में परिभाषित किया गया है, जहां पहला पैरामीटर वितरण का माध्य है और दूसरा पैरामीटर इसका मानक विचलन (या एसडी) है।

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

इसलिए मानक सामान्य वितरण का ग्राफ इस प्रकार है:

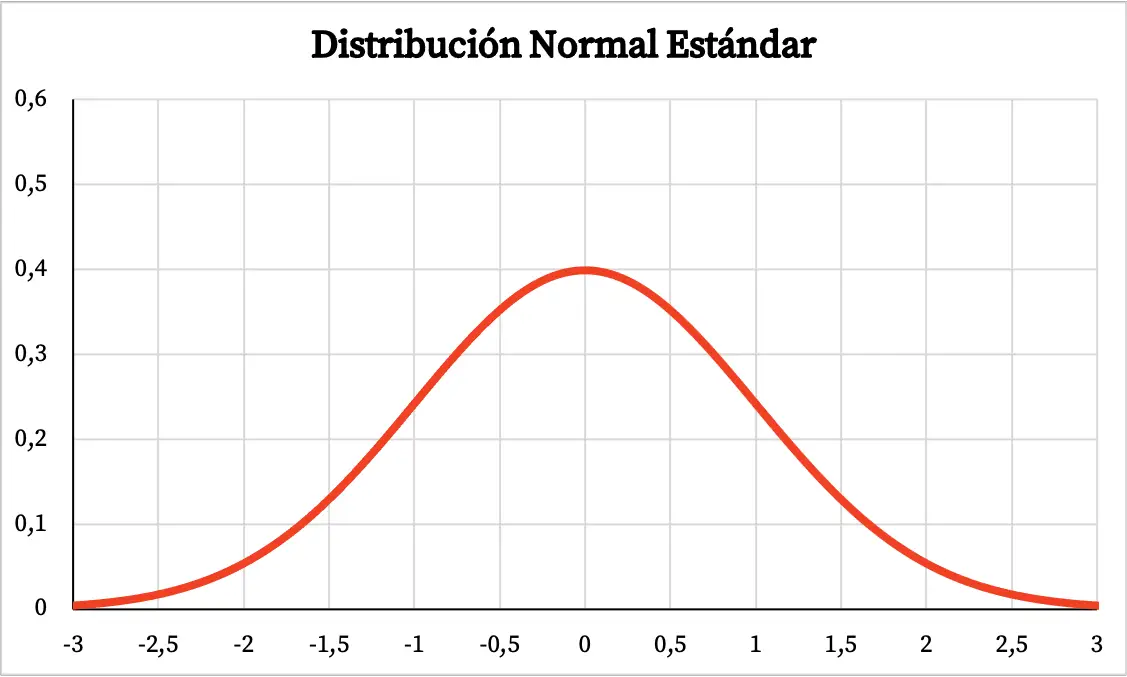
मानक सामान्य वितरण के लिए सूत्र

किसी भी सामान्य वितरण को मानक सामान्य वितरण में बदलने के लिए, आपको उसके सभी मानों से सामान्य वितरण का माध्य घटाना होगा और फिर सामान्य वितरण के मानक विचलन से विभाजित करना होगा।

इसलिए मानक सामान्य वितरण का सूत्र इस प्रकार है:

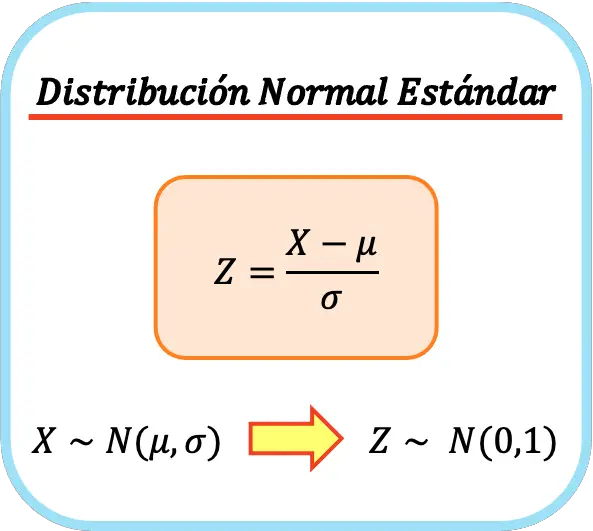
इस प्रकार, नए चर का अंकगणितीय माध्य और मानक विचलन क्रमशः 0 और 1 होगा, इसलिए हम एक मानक सामान्य वितरण प्राप्त करेंगे। इस प्रक्रिया को यूनीवेरिएट सामान्यीकरण या यूनीवेरिएट सामान्यीकरण भी कहा जाता है।

मानक सामान्य वितरण तालिका

मानक सामान्य वितरण की तालिका एक तालिका है जिसमें संभावनाएँ होती हैं कि एक मनाया गया मान मानक सामान्य वितरण के दिए गए मान से कम है।

इसके अतिरिक्त, चूंकि सामान्य वितरण का कार्य उसके माध्य और मानक विचलन पर निर्भर करता है, इसलिए किसी भी सामान्य वितरण की संभावनाओं को निर्धारित करने के लिए, विस्तार द्वारा, मानक सामान्य वितरण तालिका का भी उपयोग किया जाता है। ऐसा करने के लिए, सामान्य वितरण को मानक सामान्य वितरण में टाइप किया जाता है और फिर हम तालिका में देखते हैं कि कौन सी संभावना इसके अनुरूप है।

तो, मानक सामान्य वितरण तालिका में मान इस प्रकार हैं:

मानक सामान्य वितरण का उदाहरण

अब जब हम मानक सामान्य वितरण की परिभाषा जानते हैं और इसका सूत्र क्या है, तो अवधारणा को अच्छी तरह से समझने के लिए नीचे एक ठोस उदाहरण दिया गया है।

एक सतत यादृच्छिक चर माध्य 45 और मानक विचलन 15 के साथ एक सामान्य वितरण का अनुसरण करता है, 58 से कम या उसके बराबर मान प्राप्त करने की संभावना क्या है?

$N(45,15)\ \color{orange}\bm{\longrightarrow}\color{black}\ P[X\leq 58]= \ \color{orange}\bm{?}\color{black}$

सामान्य वितरण की संभावना जानने के लिए, हमें इसकी फीचर तालिका का उपयोग करने की आवश्यकता है, लेकिन ऐसा करने के लिए, हमें पहले मानक सामान्य वितरण प्राप्त करने के लिए टाइपिंग प्रक्रिया करने की आवश्यकता है। इसलिए हम मानक सामान्य वितरण सूत्र का उपयोग करते हैं:

$Z=\cfrac{X-\mu}{\sigma}$

इसलिए हम संभाव्यता मान से माध्य घटाते हैं और फिर मानक विचलन से विभाजित करते हैं

$\displaystyle P[X\leq 58]=P\left[Z\leq\frac{58-45}{15}\right]=P[Z\leq 0,87]$

एक बार जब हम चर को मानकीकृत कर लेते हैं, तो हम यह देखने के लिए मानक सामान्य वितरण संभाव्यता तालिका (ऊपर देखें) पर जाते हैं कि 0.87 का मान किस संभाव्यता से मेल खाता है:

$\displaystyle P[Z\leq 0,87]=0,8078$

इसलिए 58 के बराबर या उससे कम मान प्राप्त करने की संभावना 80.78% है।

मानक सामान्य वितरण के लक्षण

मानक सामान्य वितरण में निम्नलिखित विशेषताएं हैं:

मानक सामान्य वितरण 0 पर केन्द्रित एक सममित वितरण है।
सामान्य वितरण की तरह, मानक सामान्य वितरण ग्राफ़ घंटी के आकार का होता है, जिसमें अधिकांश ग्राफ़ क्षेत्र माध्य के आसपास आता है।
इसलिए, सामान्य वितरण के माध्य, बहुलक और माध्यिका का मान समान होता है, जो 0 है।
मानक सामान्य वितरण का अधिकतम मान z=0 है।
इसी प्रकार, मानक सामान्य वितरण में z=-1 और z=+1 पर दो विभक्ति बिंदु होते हैं।
अंगूठे के नियम के अनुसार, हम जानते हैं कि 68% मान +1 और -1 के बीच मानक सामान्य वितरण में आते हैं, 95% मान +2 और -2 के बीच और 99.7% मान + के बीच आते हैं। 3 और – 3.

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने