सामान्य वितरण

सांख्यिकी में सामान्य वितरण सबसे आम संभाव्यता वितरण है।

सामान्य वितरण में निम्नलिखित विशेषताएं होती हैं:

• बेल आकार
• सममित
• माध्य और मध्यिका बराबर हैं; दोनों वितरण के केंद्र में स्थित हैं
• लगभग 68% डेटा माध्य के एक मानक विचलन के अंतर्गत आता है
• लगभग 95% डेटा माध्य के दो मानक विचलनों के अंतर्गत आता है।
• लगभग 99.7% डेटा माध्य के तीन मानक विचलन के अंतर्गत आता है।

अंतिम तीन बिंदुओं को अंगूठे के नियम के रूप में जाना जाता है, जिसे कभी-कभी 68-95-99.7 नियम भी कहा जाता है।

संबंधित: अंगूठे का नियम (अभ्यास मुद्दे)

सामान्य वक्र कैसे बनाएं

एक सामान्य वक्र बनाने के लिए, हमें माध्य और मानक विचलन जानने की आवश्यकता है।

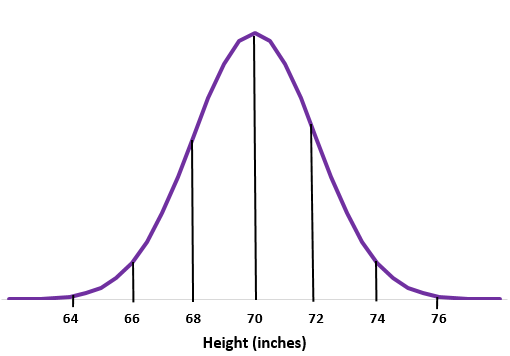
उदाहरण 1: मान लीजिए कि एक निश्चित स्कूल में पुरुषों की ऊंचाई सामान्यतः $\mu =\; 70\; इंच\; के\; माध्य\; और$ $\sigma \; =\; 2\; इंच\; के\; मानक\; विचलन\; के\; साथ\; वितरित\; की\; जाती\; है।\; सामान्य\; वक्र\; का\; रेखाचित्र\; बनाएं।$

चरण 1: एक सामान्य वक्र बनाएं।

चरण 2: मध्य में 70 इंच का औसत है।

चरण 3: प्रत्येक मानक विचलन 2 इंच की दूरी से मेल खाता है।

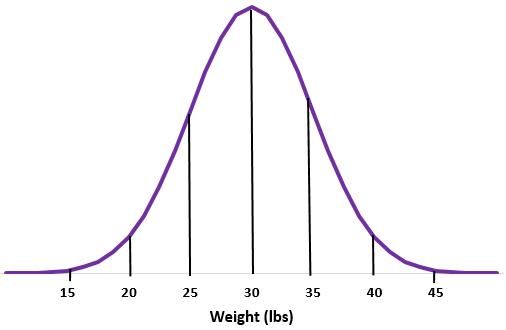
उदाहरण 2: मान लीजिए कि ऊदबिलाव की एक निश्चित प्रजाति का वजन आम तौर पर $\mu =\; 30\; पाउंड\; के\; माध्य\; और$ $\sigma \; =\; 5\; पाउंड$ के मानक विचलन के साथ वितरित किया जाता है। $सामान्य\; वक्र\; का\; रेखाचित्र\; बनाएं.$

चरण 1: एक सामान्य वक्र बनाएं।

चरण 2: 30-पाउंड का औसत बीच में आता है।

चरण 3: प्रत्येक मानक विचलन 5 पाउंड की दूरी से मेल खाता है

सामान्य वितरण का उपयोग करके प्रतिशत कैसे ज्ञात करें

अंगूठे का नियम , जिसे कभी-कभी 68-95-99.7 नियम कहा जाता है, बताता है कि सामान्य रूप से वितरित यादृच्छिक चर के लिए, 68% डेटा माध्य से एक मानक विचलन की सीमा के भीतर आता है, 95% दो मानक की सीमा के भीतर आता है। माध्य से विचलन और 99.7% माध्य से तीन मानक विचलन के भीतर हैं।

इस नियम का उपयोग करके हम प्रतिशत के बारे में प्रश्नों का उत्तर दे सकते हैं।

उदाहरण: मान लीजिए कि एक निश्चित स्कूल में पुरुषों की ऊंचाई सामान्यतः $\mu =\; 70\; इंच\; के\; माध्य\; और$ $\sigma \; =\; 2\; इंच\; के\; मानक\; विचलन\; के\; साथ\; वितरित\; की\; जाती\; है।$

$इस\; स्कूल\; में\; लगभग\; कितने\; प्रतिशत\; पुरुष\; 74\; इंच\; से\; अधिक\; लम्बे\; हैं?$

समाधान:

चरण 1: $\mu =\; 70\; इंच\; के\; माध्य\; और$ $\sigma \; =\; 2\; इंच\; के\; मानक\; विचलन\; के\; साथ\; एक\; सामान्य\; वितरण\; का\; रेखाचित्र\; बनाएं।$

चरण 2: 74 इंच की ऊंचाई औसत से दो मानक विचलन है। इस बिंदु से ऊपर के प्रतिशत को सामान्य वितरण में जोड़ें।

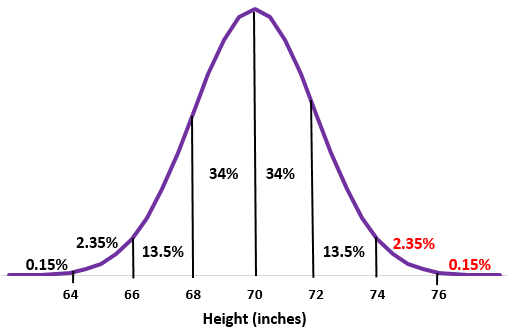
2.35% + 0.15% = 2.5%

इस स्कूल में लगभग 2.5% पुरुष 74 इंच से अधिक लंबे हैं।

$इस\; स्कूल\; में\; लगभग\; कितने\; प्रतिशत\; पुरुष\; 68\; इंच\; से\; 72\; इंच\; लंबे\; हैं?$

समाधान:

चरण 1: $\mu =\; 70\; इंच\; के\; माध्य\; और$ $\sigma \; =\; 2\; इंच\; के\; मानक\; विचलन\; के\; साथ\; एक\; सामान्य\; वितरण\; का\; रेखाचित्र\; बनाएं।$

चरण 2: 68 इंच और 72 इंच की ऊंचाई क्रमशः औसत से नीचे और ऊपर एक मानक विचलन है। बस सामान्य वितरण में इन दो बिंदुओं के बीच प्रतिशत जोड़ें।

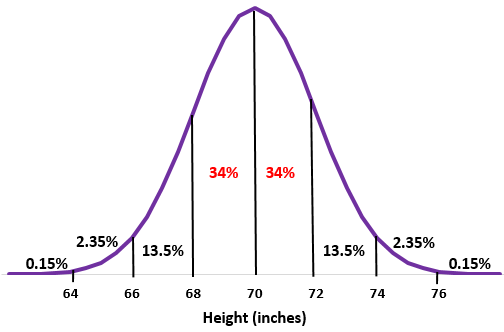
34% + 34% = 68%

इस स्कूल में लगभग 68% पुरुषों की लंबाई 68 इंच से 72 इंच के बीच है।

सामान्य वितरण का उपयोग करके गिनती कैसे ज्ञात करें

गिनती के बारे में प्रश्नों का उत्तर देने के लिए हम अंगूठे के नियम का भी उपयोग कर सकते हैं।

उदाहरण: मान लीजिए कि ऊदबिलाव की एक निश्चित प्रजाति का वजन आम तौर पर $\mu =\; 30\; पाउंड\; के\; माध्य\; और$ $\sigma \; =\; 5\; पाउंड$ के मानक विचलन के साथ वितरित किया जाता है।

एक निश्चित कॉलोनी में ऐसे 200 ऊदबिलाव हैं। इनमें से लगभग कितने ऊदबिलावों का वजन 35 पाउंड से अधिक है?

समाधान:

चरण 1: $\mu =\; 30\; lb\; के\; माध्य\; और$ $\sigma \; =\; 5\; lb$ के मानक विचलन के साथ एक सामान्य वितरण का रेखाचित्र बनाएं।

चरण 2: 35 पाउंड का वजन माध्य से एक मानक विचलन है। इस बिंदु से ऊपर के प्रतिशत को सामान्य वितरण में जोड़ें।

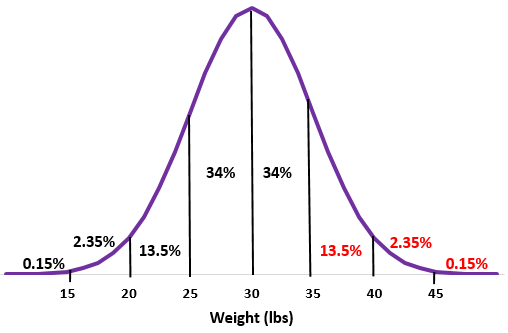
13.5% + 2.35% + 0.15% = 16%

चरण 3: चूंकि कॉलोनी में 200 ऊदबिलाव हैं, 200 का 16% = 0.16 * 200 = 32

इस कॉलोनी में लगभग 32 ऊदबिलावों का वजन 35 पाउंड से अधिक है।

इस कॉलोनी में लगभग कितने ऊदबिलावों का वजन 30 पाउंड से कम है?

हमारे द्वारा ऊपर उठाए गए सभी चरणों का पालन करने के बजाय, हम यह पहचान सकते हैं कि सामान्य वितरण का माध्य माध्य के बराबर है, जो इस मामले में 30 पाउंड है।

इसका मतलब है कि आधे ऊदबिलावों का वजन 30 पाउंड से अधिक है और दूसरे आधे का वजन 30 पाउंड से कम है। इसका मतलब है कि 200 ऊदबिलावों में से 50% का वजन 30 पाउंड से कम है, इसलिए 0.5 * 200 = 100 ऊदबिलाव ।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल सामान्य वितरण के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

सामान्य वितरण के 6 ठोस उदाहरण
सामान्य वितरण बनाम टी वितरण: अंतर
एक्सेल में बेल कर्व कैसे बनाएं
पायथन में बेल कर्व कैसे बनाएं