स्पीयरमैन रैंक सहसंबंध का उपयोग कब करें (2 परिदृश्य)

दो चरों के बीच रैखिक संबंध को मापने का सबसे आम तरीका पियर्सन सहसंबंध गुणांक का उपयोग करना है, जो हमेशा -1 और 1 के बीच मान लेता है:

• -1 पूर्णतः नकारात्मक रैखिक सहसंबंध दर्शाता है
• 0 कोई रैखिक सहसंबंध नहीं दर्शाता है
• 1 पूर्णतः सकारात्मक रैखिक सहसंबंध दर्शाता है

हालाँकि, इस प्रकार का सहसंबंध गुणांक सबसे अच्छा काम करता है जब दो चर के बीच वास्तविक अंतर्निहित संबंध रैखिक होता है।

एक अन्य प्रकार का सहसंबंध गुणांक है जिसे स्पीयरमैन रैंक सहसंबंध कहा जाता है जिसका दो विशिष्ट परिदृश्यों में सबसे अच्छा उपयोग किया जाता है:

परिदृश्य 1 : वर्गीकृत डेटा के साथ काम करते समय।

• एक उदाहरण एक डेटासेट हो सकता है जिसमें किसी छात्र के गणित परीक्षा स्कोर की रैंकिंग के साथ-साथ कक्षा में उनके विज्ञान परीक्षा स्कोर की रैंकिंग भी शामिल हो।

परिदृश्य 2 : जब एक या अधिक चरम आउटलेर मौजूद हों।

• जब डेटा सेट में चरम आउटलेर्स मौजूद होते हैं, तो पियर्सन सहसंबंध गुणांक बहुत प्रभावित होता है।

निम्नलिखित उदाहरण दिखाते हैं कि इनमें से प्रत्येक परिदृश्य में स्पीयरमैन रैंक सहसंबंध की गणना कैसे करें।

परिदृश्य 1: स्पीयरमैन रैंकिंग को रैंक किए गए डेटा के साथ सहसंबंधित करना

निम्नलिखित डेटा सेट (और संबंधित स्कैटरप्लॉट) पर विचार करें जो दो चर के बीच संबंध दिखाता है:

सांख्यिकीय सॉफ़्टवेयर का उपयोग करके, हम इन दो चरों के लिए निम्नलिखित सहसंबंध गुणांक की गणना कर सकते हैं:

• पियर्सन सहसंबंध: 0.79
• स्पीयरमैन रैंक सहसंबंध: 1

इस परिदृश्य में, यदि हम केवल डेटा मानों की रैंक की परवाह करते हैं (जैसे-जैसे x की रैंक बढ़ती है, क्या y की रैंक भी बढ़ती है?), तो स्पीयरमैन का रैंक सहसंबंध हमें इसका बेहतर विचार देगा दो चरों के बीच सहसंबंध. .

इस विशेष डेटासेट में, जैसे-जैसे x की रैंक बढ़ती है, y की रैंक भी हमेशा बढ़ती है।

स्पीयरमैन का रैंक सहसंबंध हमें यह बताकर इस व्यवहार को पूरी तरह से पकड़ लेता है कि x के रैंक और y के रैंक के बीच एक पूर्ण सकारात्मक संबंध ( ρ = 1 ) है।

दूसरी ओर, पियर्सन सहसंबंध हमें बताता है कि दो चरों के बीच एक मजबूत रैखिक संबंध ( r = 0.79 ) है।

यह सच है, लेकिन यह उपयोगी नहीं है अगर हम केवल x की रैंक और y की रैंक के बीच संबंध की परवाह करते हैं।

परिदृश्य 2: अत्यधिक आउटलेर्स के साथ स्पीयरमैन रैंकिंग का सहसंबंध

निम्नलिखित डेटा सेट (और संबंधित स्कैटरप्लॉट) पर विचार करें जो दो चर के बीच संबंध दिखाता है:

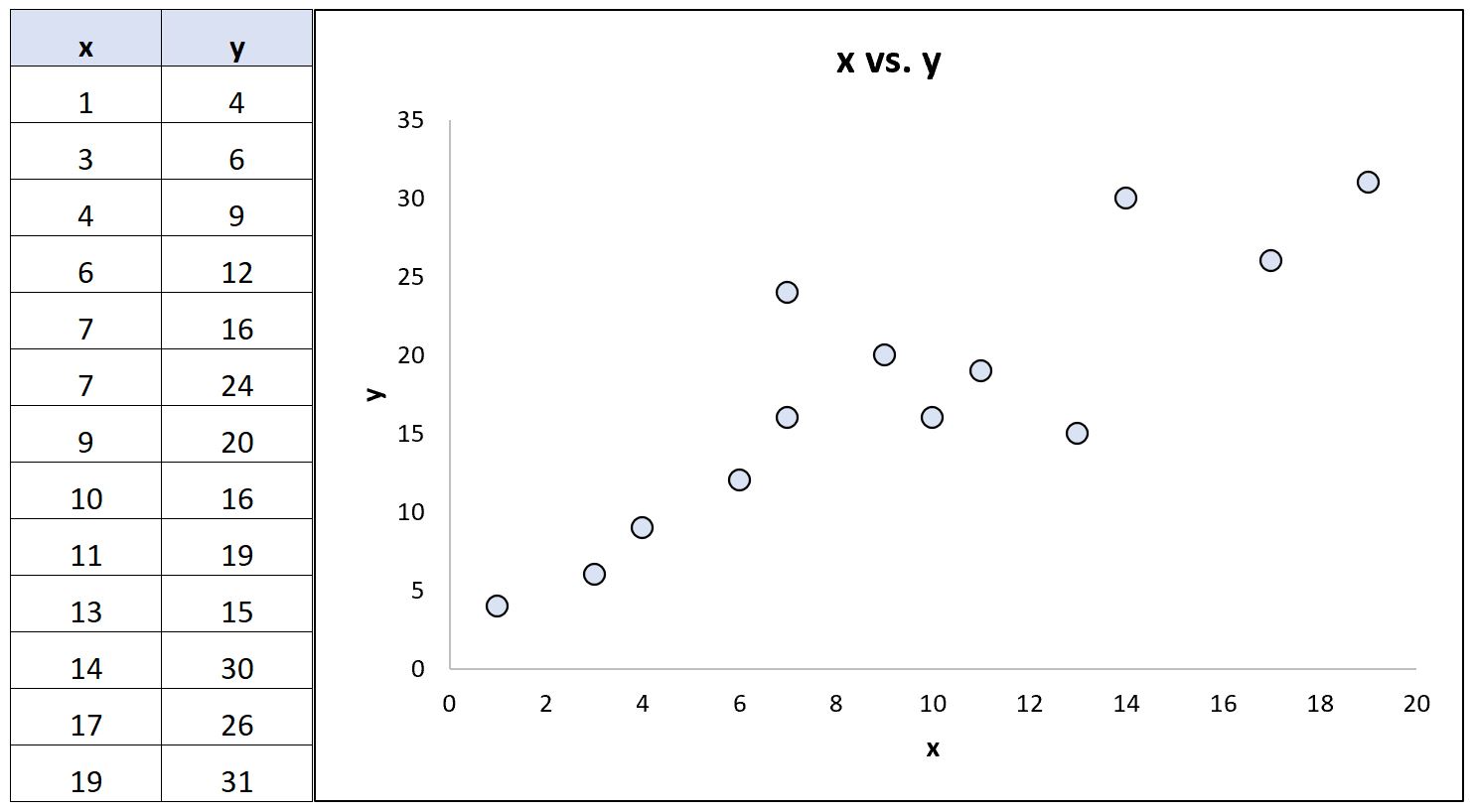
सांख्यिकीय सॉफ़्टवेयर का उपयोग करके, हम इन दो चरों के लिए निम्नलिखित सहसंबंध गुणांक की गणना कर सकते हैं:

• पियर्सन सहसंबंध: 0.86
• स्पीयरमैन रैंक सहसंबंध: 0.85

सहसंबंध गुणांक लगभग समान हैं क्योंकि चर के बीच अंतर्निहित संबंध लगभग रैखिक है और कोई चरम आउटलेर नहीं हैं।

अब मान लीजिए कि हम डेटासेट में अंतिम y मान को बदल देते हैं ताकि यह अत्यधिक बाहरी हो जाए:

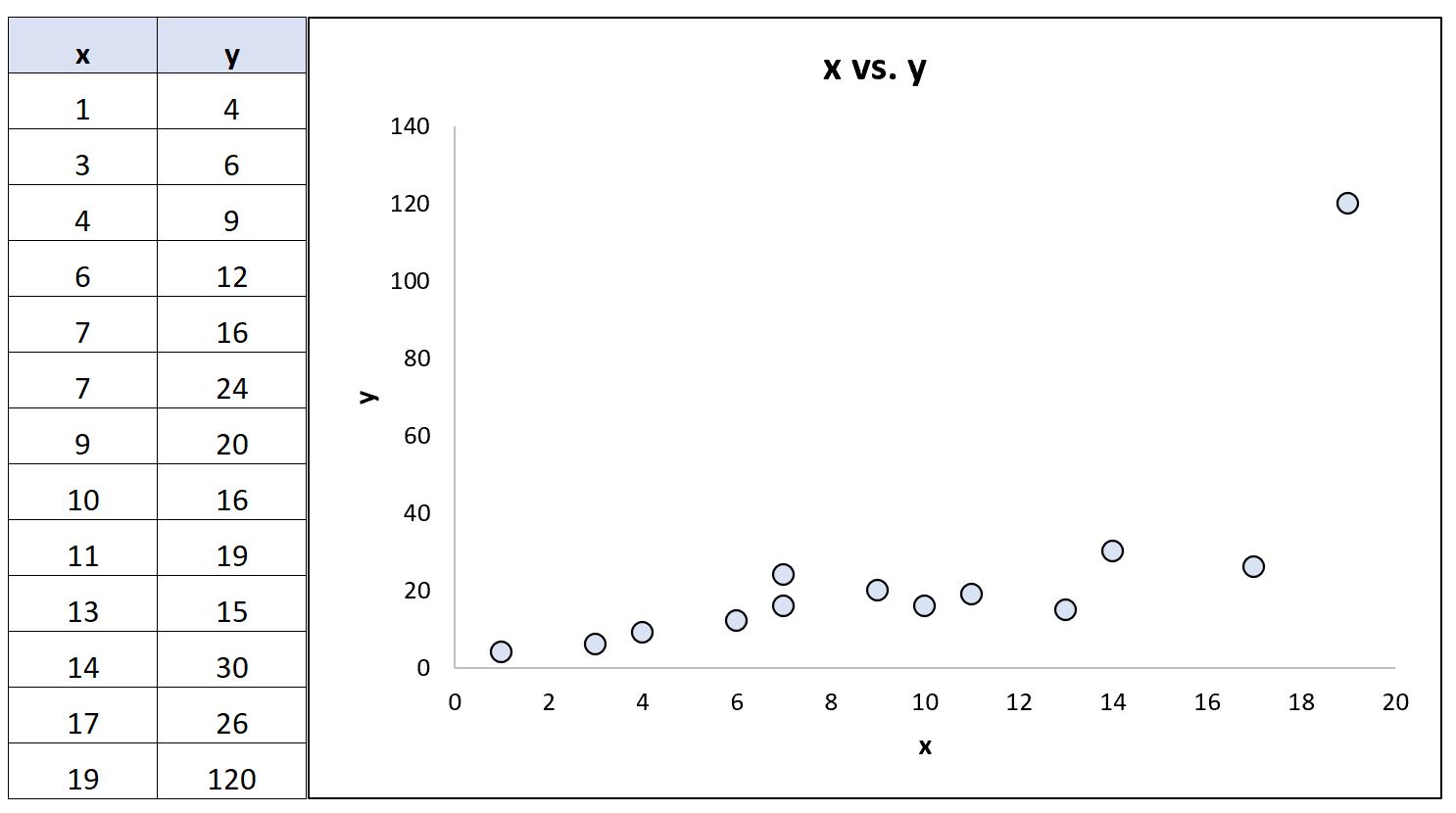
सांख्यिकीय सॉफ़्टवेयर का उपयोग करके, हम सहसंबंध गुणांकों की पुनर्गणना कर सकते हैं:

• पियर्सन सहसंबंध: 0.69
• स्पीयरमैन रैंक सहसंबंध: 0.85

पियर्सन सहसंबंध गुणांक में काफी बदलाव आया जबकि स्पीयरमैन रैंक सहसंबंध गुणांक वही रहा।

सांख्यिकीय शब्दजाल का उपयोग करते हुए, हम कहेंगे कि x और y के बीच संबंधएकरस है (जैसे-जैसे x बढ़ता है, y आम तौर पर बढ़ता है) लेकिन रैखिक नहीं है क्योंकि बाहरी डेटा को बहुत प्रभावित करता है।

इस परिदृश्य में, स्पीयरमैन का रैंक सहसंबंध इस एकरस संबंध को अच्छी तरह से मापता है, जबकि पियर्सन का सहसंबंध खराब काम करता है क्योंकि यह दो चर के बीच रैखिक संबंध की गणना करने का प्रयास करता है।

संबंधित: एपीए प्रारूप में स्पीयरमैन रैंक सहसंबंध की रिपोर्ट कैसे करें

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि विभिन्न सॉफ़्टवेयर का उपयोग करके स्पीयरमैन रैंक सहसंबंध की गणना कैसे करें:

एक्सेल में स्पीयरमैन रैंक सहसंबंध की गणना कैसे करें
Google शीट्स में स्पीयरमैन रैंक सहसंबंध की गणना कैसे करें
आर में स्पीयरमैन रैंक सहसंबंध की गणना कैसे करें
पायथन में स्पीयरमैन रैंक सहसंबंध की गणना कैसे करें