हिस्टोग्राम की तुलना कैसे करें (उदाहरण के साथ)

हिस्टोग्राम एक प्रकार का चार्ट है जो हमें डेटा के एक सेट में मूल्यों के वितरण की कल्पना करने की अनुमति देता है।

X-अक्ष डेटासेट के मान दिखाता है और Y-अक्ष प्रत्येक मान की आवृत्ति दिखाता है।

हिस्टोग्राम उपयोगी होते हैं क्योंकि वे हमें डेटा सेट में मूल्यों के वितरण को तुरंत समझने की अनुमति देते हैं। वे दो अलग-अलग डेटा सेटों की तुलना करने के लिए भी उपयोगी हैं।

दो या दो से अधिक हिस्टोग्राम की तुलना करते समय, हम तीन अलग-अलग प्रश्नों का उत्तर दे सकते हैं:

1. माध्यिका मानों की तुलना कैसे की जाती है?

हम मोटे तौर पर अनुमान लगा सकते हैं कि माध्यिका प्रत्येक हिस्टोग्राम के मध्य के पास स्थित है, जिससे हमें वितरण के माध्य मूल्यों की तुलना करने की अनुमति मिलती है।

2. फैलाव की तुलना कैसे की जाती है?

हम दृश्य रूप से देख सकते हैं कि कौन सा हिस्टोग्राम अधिक फैला हुआ है, जिससे हमें यह पता चलता है कि किस वितरण में अधिक बिखरे हुए मूल्य हैं।

3. विषमता की तुलना कैसे की जाती है?

यदि हिस्टोग्राम में कथानक के बाईं ओर एक “पूंछ” है, तो इसे नकारात्मक रूप से तिरछा कहा जाता है। इसके विपरीत, यदि हिस्टोग्राम में कथानक के दाईं ओर एक “पूंछ” है, तो इसे सकारात्मक रूप से तिरछा कहा जाता है। हम तिरछापन की तुलना करने के लिए प्रत्येक हिस्टोग्राम को दृष्टिगत रूप से जांच सकते हैं।

निम्नलिखित उदाहरण दिखाता है कि दो अलग-अलग हिस्टोग्राम की तुलना कैसे करें और इन तीन प्रश्नों के उत्तर कैसे दें।

उदाहरण: हिस्टोग्राम की तुलना करना

मान लें कि 200 छात्र एक परीक्षा की तैयारी के लिए एक अध्ययन पद्धति का उपयोग करते हैं और अन्य 200 छात्र उसी परीक्षा की तैयारी के लिए एक अलग अध्ययन पद्धति का उपयोग करते हैं।

मान लीजिए कि हम छात्रों के प्रत्येक समूह के परीक्षा परिणामों की तुलना करने के लिए निम्नलिखित हिस्टोग्राम बनाते हैं:

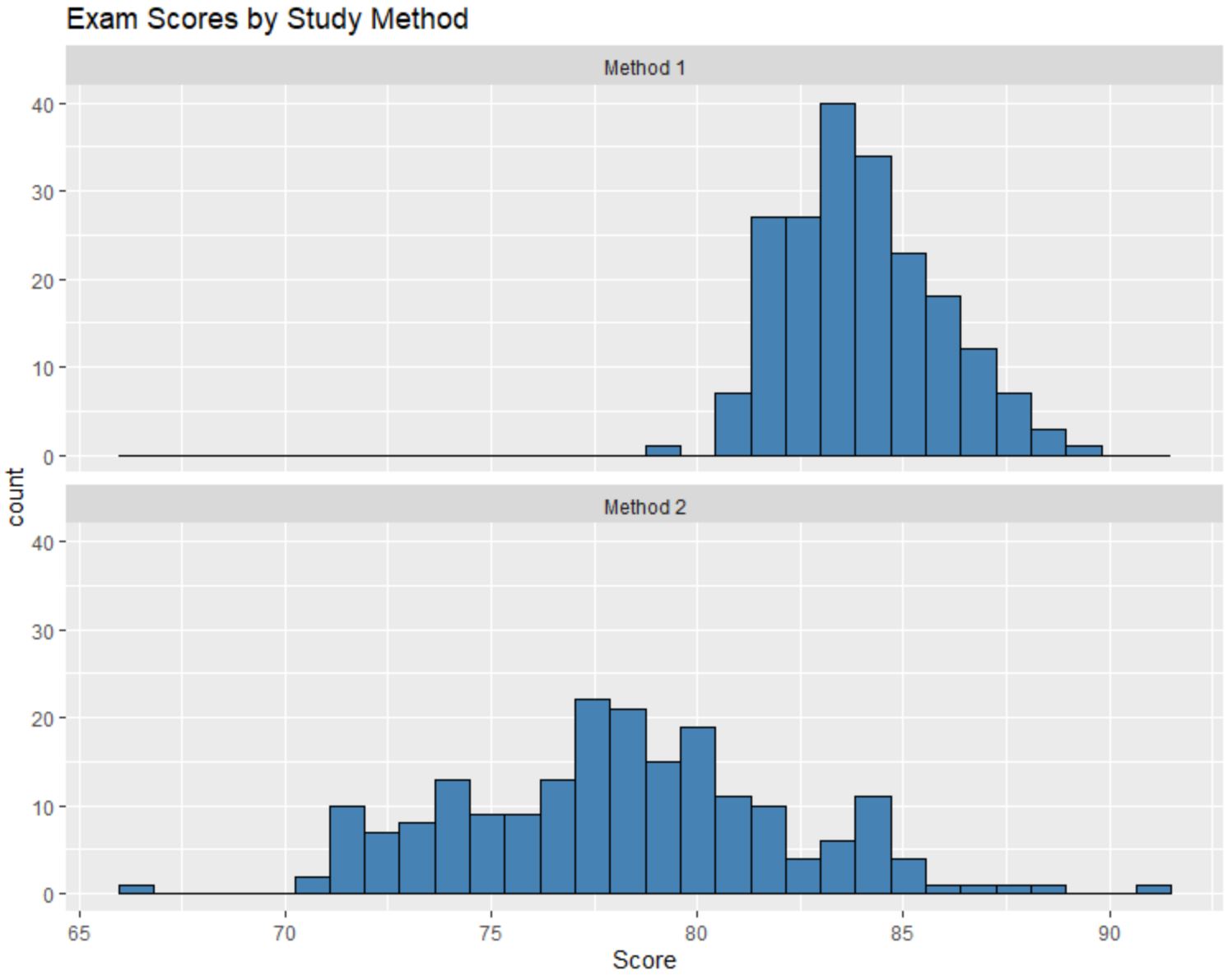
हम इन हिस्टोग्राम की तुलना कर सकते हैं और निम्नलिखित तीन प्रश्नों के उत्तर दे सकते हैं:

1. माध्यिका मानों की तुलना कैसे की जाती है?

यद्यपि हम केवल हिस्टोग्राम को देखकर प्रत्येक वितरण के सटीक औसत मूल्यों को नहीं जानते हैं, यह स्पष्ट है कि विधि 1 का उपयोग करने वाले छात्रों का औसत परीक्षा स्कोर विधि 1 का उपयोग करने वाले छात्रों के औसत परीक्षा स्कोर से अधिक है। विधि 2.

हम अनुमान लगा सकते हैं कि विधि 1 के लिए माध्य मान लगभग 84 है और विधि 2 के लिए माध्य मान लगभग 78 है।

2. फैलाव की तुलना कैसे की जाती है?

विधि 2 के लिए हिस्टोग्राम मान विधि 1 की तुलना में बहुत अधिक बिखरे हुए हैं, जो हमें बताता है कि विधि 2 का उपयोग करने वाले छात्रों के परीक्षा परिणामों में बहुत अधिक बिखराव है।

3. विषमता की तुलना कैसे की जाती है?

हिस्टोग्राम को देखने पर ऐसा प्रतीत होता है कि विधि 1 के लिए परीक्षण अंकों का वितरण दाईं ओर थोड़ा तिरछा है, जैसा कि हिस्टोग्राम के दाईं ओर फैली हुई “पूंछ” से संकेत मिलता है।

हालाँकि, विधि 2 के लिए परीक्षा परिणामों के वितरण में कोई “पूंछ” दिखाई नहीं देती है, जो हमें बताती है कि वितरण कम है या विषम नहीं है।

बोनस : यहां वह कोड है जिसका उपयोग हमने इन दो हिस्टोग्राम बनाने के लिए आर में किया था:

 library (ggplot2)

#make this example reproducible
set. seeds (0)

#create data frame
df <- data. frame (method=rep(c(' Method 1 ', ' Method 2 '), each= 200 ),
                 Score=c(rnorm( 200 , mean= 84 , sd= 2 ),
                         rnorm( 200 , mean= 78 , sd= 4 )))

#create histogram of scores for each method
ggplot(df, aes(x=Score)) +
  geom_histogram(fill=' steelblue ', color=' black ') +
  facet_wrap(.~method, nrow= 2 ) +
  labs(title=' Exam Scores by Study Method ')

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि हिस्टोग्राम के साथ अन्य सामान्य कार्य कैसे करें:

किसी हिस्टोग्राम के माध्य और माध्यिका का अनुमान कैसे लगाएं
किसी हिस्टोग्राम के मानक विचलन का अनुमान कैसे लगाएं
हिस्टोग्राम के आकार का वर्णन कैसे करें