एक संपूर्ण मार्गदर्शिका: 2×4 फैक्टोरियल डिज़ाइन

2 × 4 फ़ैक्टोरियल डिज़ाइन एक प्रकार का प्रायोगिक डिज़ाइन है जो शोधकर्ताओं को एक एकल आश्रित चर पर दो स्वतंत्र चर के प्रभावों को समझने की अनुमति देता है।

इस प्रकार के डिज़ाइन में, एक स्वतंत्र चर के दो स्तर होते हैं और दूसरे स्वतंत्र चर के चार स्तर होते हैं।

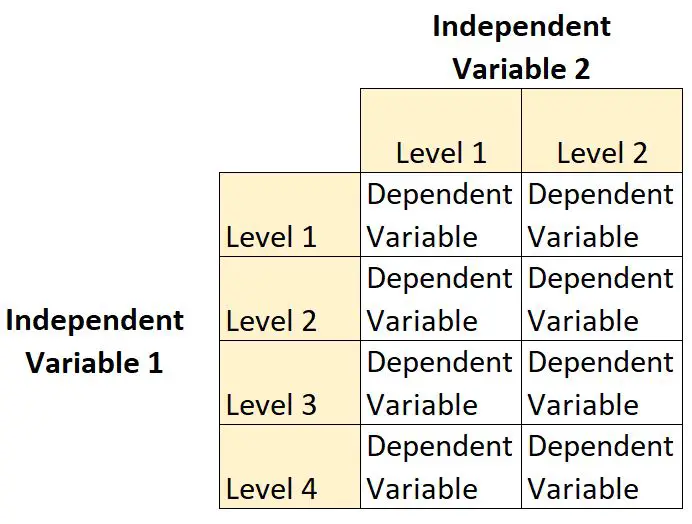
उदाहरण के लिए, मान लीजिए कि एक वनस्पतिशास्त्री एक निश्चित पौधे की प्रजाति के विकास पर सूर्य के प्रकाश (कोई नहीं, कम, मध्यम या उच्च) और पानी की आवृत्ति (दैनिक या साप्ताहिक) के प्रभाव को समझना चाहता है।

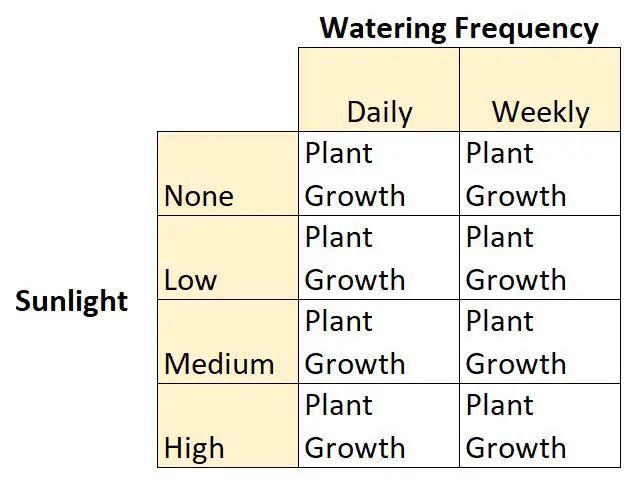
यह 2 × 4 फ़ैक्टोरियल डिज़ाइन का एक उदाहरण है क्योंकि इसमें दो स्वतंत्र चर हैं, एक दो स्तरों वाला और एक चार स्तरों वाला:

• स्वतंत्र चर #1: सूर्य का प्रकाश
  • स्तर: कोई नहीं, निम्न, मध्यम, उच्च
• स्वतंत्र चर #2: पानी देने की आवृत्ति
  • स्तर: दैनिक, साप्ताहिक

और एक आश्रित चर है: पौधे की वृद्धि।

2 × 4 फ़ैक्टोरियल डिज़ाइन का उद्देश्य

2×4 फ़ैक्टोरियल डिज़ाइन निम्नलिखित प्रभावों का विश्लेषण करना संभव बनाता है:

मुख्य प्रभाव: ये वे प्रभाव हैं जो एक स्वतंत्र चर का आश्रित चर पर पड़ता है।

उदाहरण के लिए, हमारे पिछले परिदृश्य में, हम निम्नलिखित मुख्य प्रभावों का विश्लेषण कर सकते हैं:

• सूर्य के प्रकाश का मुख्य प्रभाव पौधों की वृद्धि पर पड़ता है।
  • उन सभी पौधों की औसत वृद्धि जिन्हें सूर्य की रोशनी नहीं मिली।
  • कम धूप प्राप्त करने वाले सभी पौधों की औसत वृद्धि।
  • उन सभी पौधों की औसत वृद्धि जिन्हें औसत सूर्य का प्रकाश प्राप्त हुआ।
  • उन सभी पौधों की औसत वृद्धि जिन्हें तेज़ धूप प्राप्त हुई।
• पौधों की वृद्धि पर पानी देने की आवृत्ति का मुख्य प्रभाव।
  • प्रतिदिन पानी देने वाले सभी पौधों की औसत वृद्धि।
  • प्रत्येक सप्ताह पानी दिए गए सभी पौधों की औसत वृद्धि।

अंतःक्रिया प्रभाव: वे तब घटित होते हैं जब एक स्वतंत्र चर का आश्रित चर पर प्रभाव दूसरे स्वतंत्र चर के स्तर पर निर्भर करता है।

उदाहरण के लिए, हमारे पिछले परिदृश्य में, हम निम्नलिखित इंटरैक्शन प्रभावों का विश्लेषण कर सकते हैं:

• क्या पौधों की वृद्धि पर सूर्य के प्रकाश का प्रभाव पानी देने की आवृत्ति पर निर्भर करता है?
• क्या पौधों की वृद्धि पर पानी देने की आवृत्ति का प्रभाव सूर्य के प्रकाश पर निर्भर करता है?

2 × 4 फ़ैक्टोरियल डिज़ाइन का विश्लेषण कैसे करें

हम औपचारिक रूप से परीक्षण करने के लिए दो-तरफ़ा एनोवा का प्रदर्शन कर सकते हैं कि स्वतंत्र चर का आश्रित चर के साथ सांख्यिकीय रूप से महत्वपूर्ण संबंध है या नहीं।

उदाहरण के लिए, निम्नलिखित कोड दिखाता है कि आर में हमारे काल्पनिक फ़ैक्टरी परिदृश्य के लिए दो-तरफ़ा एनोवा कैसे निष्पादित करें:

 #make this example reproducible
set. seeds (0)

#createdata
df <- data. frame (sunlight = rep(c(' None ', ' Low ', ' Medium ', ' High '), each= 10 , times= 2 ),
                 water = rep(c(' Daily ', ' Weekly '), each= 40 , times= 2 ),
                 growth = c(rnorm(10, 8, 2), rnorm(10, 8, 3), rnorm(10, 13, 2),
                            rnorm(10, 14, 3), rnorm(10, 10, 4), rnorm(10, 12, 3),
                            rnorm(10, 13, 2), rnorm(10, 14, 4)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

                Df Sum Sq Mean Sq F value Pr(>F)    
sunlight 3 744.1 248.04 34.16 < 2e-16 ***
water 1 43.1 43.05 5.93 0.016 *  
sunlight:water 3 195.8 65.27 8.99 1.61e-05 ***
Residuals 152 1103.5 7.26                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

यहां एनोवा परिणाम की व्याख्या करने का तरीका बताया गया है:

मुख्य प्रभाव #1 (सूरज की रोशनी) : सूरज की रोशनी से जुड़ा पी-मान <2e-16 है। चूँकि यह संख्या 0.05 से कम है, इसका मतलब है कि सूर्य के प्रकाश के संपर्क में आने से पौधों की वृद्धि पर सांख्यिकीय रूप से महत्वपूर्ण प्रभाव पड़ता है।

मुख्य प्रभाव #2 (पानी) : पानी से जुड़ा पी-मान 0.016 है। चूंकि यह आंकड़ा 0.05 से कम है, इसका मतलब है कि पानी देने की आवृत्ति का भी पौधों की वृद्धि पर सांख्यिकीय रूप से महत्वपूर्ण प्रभाव पड़ता है।

अन्योन्यक्रिया प्रभाव : सूर्य के प्रकाश और पानी के बीच अन्योन्यक्रिया के लिए पी-मान 0.000061 है। चूँकि यह मान 0.05 से कम है, इसका मतलब है कि सूर्य के प्रकाश और पानी के बीच परस्पर क्रिया प्रभाव होता है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल प्रायोगिक डिजाइन और विश्लेषण पर अतिरिक्त जानकारी प्रदान करते हैं:

एक संपूर्ण मार्गदर्शिका: 2 × 2 फैक्टोरियल डिज़ाइन
एक संपूर्ण मार्गदर्शिका: 2 × 3 फैक्टोरियल डिज़ाइन
फैक्टोरियल एनोवा क्या है?