आर में तुकी परीक्षण कैसे करें
एक-तरफ़ा एनोवा का उपयोग यह निर्धारित करने के लिए किया जाता है कि तीन या अधिक स्वतंत्र समूहों के साधनों के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है या नहीं।
यदि एनोवा तालिका का समग्र पी-मूल्य एक निश्चित स्तर के महत्व से नीचे है, तो हमारे पास यह कहने के लिए पर्याप्त सबूत हैं कि समूह का कम से कम एक साधन दूसरों से अलग है।
हालाँकि, इससे हमें यह नहीं पता चलता कि कौन से समूह एक-दूसरे से भिन्न हैं। यह हमें बस इतना बताता है कि सभी समूहों का औसत समान नहीं है। यह जानने के लिए कि कौन से समूह एक-दूसरे से भिन्न हैं, हमें एक पोस्ट हॉक परीक्षण करने की आवश्यकता है।
सबसे अधिक उपयोग किए जाने वाले पोस्ट हॉक परीक्षणों में से एक तुकी परीक्षण है, जो हमें परिवारवार त्रुटि दर को नियंत्रित करते हुए प्रत्येक समूह के साधनों के बीच जोड़ीवार तुलना करने की अनुमति देता है।
यह ट्यूटोरियल बताता है कि R में Tukey परीक्षण कैसे करें।
नोट: यदि आपके अध्ययन में किसी भी समूह को नियंत्रण समूह माना जाता है, तो आपको इसके बजाय पोस्ट-हॉक परीक्षण के रूप में डननेट के परीक्षण का उपयोग करना चाहिए।
उदाहरण: आर में तुकी परीक्षण
चरण 1: एनोवा मॉडल फिट करें।
निम्नलिखित कोड दिखाता है कि तीन समूहों (ए, बी, और सी) के साथ एक नकली डेटा सेट कैसे बनाया जाए और यह निर्धारित करने के लिए डेटा में एक-तरफ़ा एनोवा मॉडल फिट किया जाए कि प्रत्येक समूह का औसत मान बराबर है या नहीं:
#make this example reproducible set.seed(0) #create data data <- data.frame(group = rep (c("A", "B", "C"), each = 30), values = c(runif(30, 0, 3), runif(30, 0, 5), runif(30, 1, 7))) #view first six rows of data head(data) group values 1 A 2.6900916 2 A 0.7965260 3 A 1.1163717 4 A 1.7185601 5 A 2.7246234 6 A 0.6050458 #fit one-way ANOVA model model <- aov (values~group, data=data) #view the model output summary(model) Df Sum Sq Mean Sq F value Pr(>F) group 2 98.93 49.46 30.83 7.55e-11 *** Residuals 87 139.57 1.60 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
हम देख सकते हैं कि एनोवा तालिका से कुल पी-वैल्यू 7.55e-11 है। चूँकि यह संख्या 0.05 से कम है, हमारे पास यह कहने के लिए पर्याप्त सबूत हैं कि प्रत्येक समूह में औसत मान समान नहीं हैं। इसलिए, हम यह निर्धारित करने के लिए टुकी परीक्षण कर सकते हैं कि वास्तव में कौन से समूह के साधन भिन्न हैं।
चरण 2: तुकी परीक्षण करें।
निम्नलिखित कोड दिखाता है कि Tukey परीक्षण करने के लिए TukeyHSD() फ़ंक्शन का उपयोग कैसे करें:
#perform Tukey's Test TukeyHSD(model, conf.level= .95 ) Tukey multiple comparisons of means 95% family-wise confidence level Fit: aov(formula = values ~ group, data = data) $group diff lwr upr p adj BA 0.9777414 0.1979466 1.757536 0.0100545 CA 2.5454024 1.7656076 3.325197 0.0000000 CB 1.5676610 0.7878662 2.347456 0.0000199
पी-वैल्यू इंगित करता है कि प्रत्येक प्रोग्राम के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है या नहीं। नतीजे बताते हैं कि 0.05 महत्व स्तर पर प्रत्येक कार्यक्रम के औसत वजन घटाने के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है।
विशेष रूप से:
- बी और ए के बीच के अंतर के लिए पी मान: 0.0100545
- C और A के बीच के अंतर के लिए P मान: 0.0000000
- सी और बी के बीच के अंतर के लिए पी मान: 0.0000199
चरण 3: परिणामों की कल्पना करें।
हम कॉन्फिडेंस अंतराल को देखने के लिए प्लॉट(TukeyHSD()) फ़ंक्शन का भी उपयोग कर सकते हैं:
#plot confidence intervals plot(TukeyHSD(model, conf.level= .95 ), las = 2 )
ध्यान दें: लास तर्क निर्दिष्ट करता है कि टिक लेबल अक्ष पर लंबवत (लास = 2) होना चाहिए।
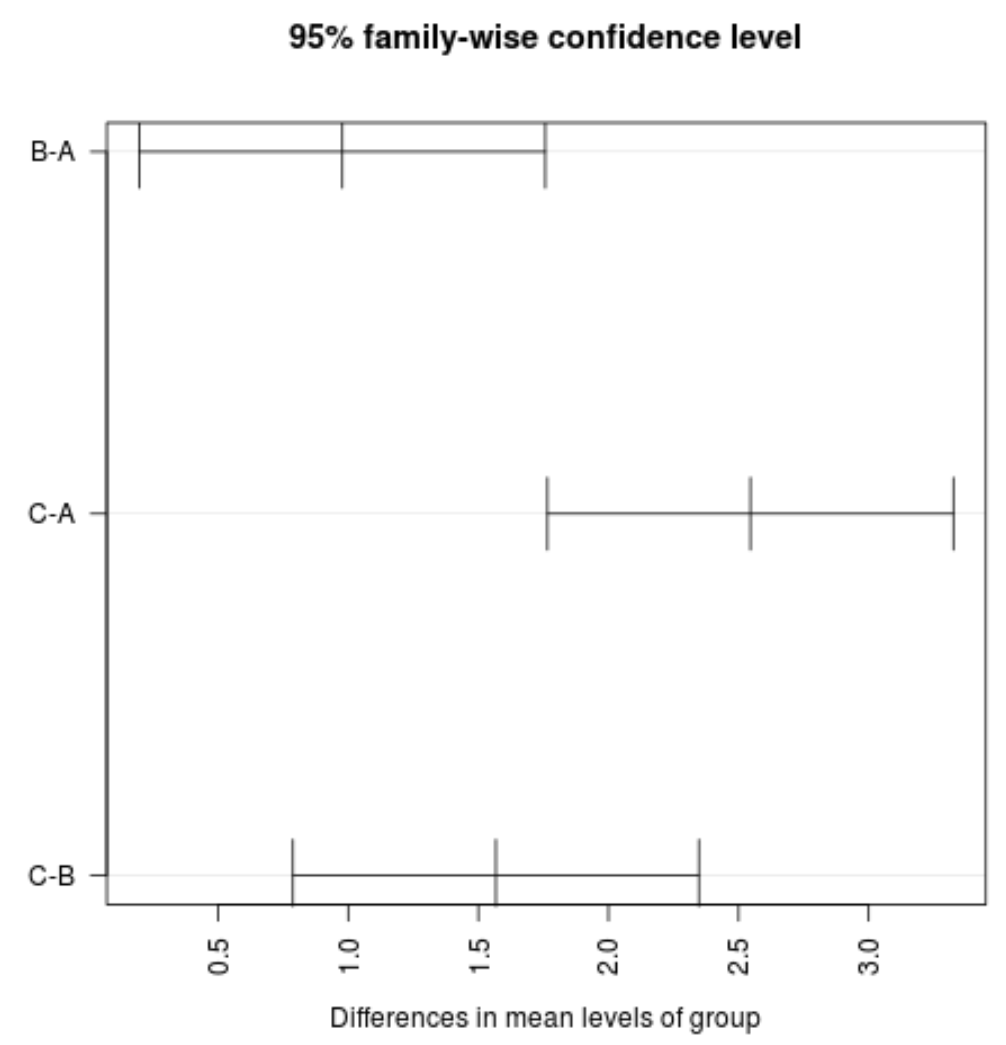
हम देख सकते हैं कि समूहों के बीच माध्य मान के लिए किसी भी विश्वास अंतराल में शून्य मान नहीं है, जो दर्शाता है कि तीन समूहों के बीच माध्य हानि में सांख्यिकीय रूप से महत्वपूर्ण अंतर है। यह हमारे परिकल्पना परीक्षणों के लिए 0.05 से कम होने वाले सभी पी-मानों के अनुरूप है।
इस विशेष उदाहरण के लिए, हम निम्नलिखित निष्कर्ष निकाल सकते हैं:
- समूह C का औसत मान समूह A और B के औसत मान से काफी अधिक है।
- समूह बी का औसत मान समूह ए के औसत मान से काफी अधिक है।
अतिरिक्त संसाधन
एनोवा के साथ पोस्ट-हॉक परीक्षण का उपयोग करने के लिए एक गाइड
आर में एकतरफ़ा एनोवा कैसे निष्पादित करें
आर में दो-तरफा एनोवा कैसे निष्पादित करें