आर में आंशिक न्यूनतम वर्ग (चरण दर चरण)

मशीन लर्निंग में आपके सामने आने वाली सबसे आम समस्याओं में से एक बहुसंरेखता है। ऐसा तब होता है जब किसी डेटा सेट में दो या दो से अधिक भविष्यवक्ता चर अत्यधिक सहसंबद्ध होते हैं।

जब ऐसा होता है, तो एक मॉडल एक प्रशिक्षण डेटा सेट को अच्छी तरह से फिट करने में सक्षम हो सकता है, लेकिन यह एक नए डेटा सेट पर खराब प्रदर्शन कर सकता है जिसे उसने कभी नहीं देखा है क्योंकि यह प्रशिक्षण डेटा सेट से अधिक फिट बैठता है । प्रशिक्षण सेट।

इस समस्या से निजात पाने का एक तरीका आंशिक न्यूनतम वर्ग नामक विधि का उपयोग करना है, जो निम्नानुसार काम करती है:

• भविष्यवक्ता और प्रतिक्रिया चर को मानकीकृत करें।
• पी मूल भविष्यवक्ता चर के एम रैखिक संयोजनों (जिन्हें “पीएलएस घटक” कहा जाता है) की गणना करें जो प्रतिक्रिया चर और भविष्यवक्ता चर दोनों में महत्वपूर्ण मात्रा में भिन्नता की व्याख्या करते हैं।
• भविष्यवक्ताओं के रूप में पीएलएस घटकों का उपयोग करके एक रेखीय प्रतिगमन मॉडल को फिट करने के लिए कम से कम वर्ग विधि का उपयोग करें।
• मॉडल में रखने के लिए पीएलएस घटकों की इष्टतम संख्या खोजने के लिए के-फोल्ड क्रॉस-सत्यापन का उपयोग करें ।

यह ट्यूटोरियल चरण-दर-चरण उदाहरण प्रदान करता है कि आर में आंशिक न्यूनतम वर्ग कैसे निष्पादित करें।

चरण 1: आवश्यक पैकेज लोड करें

R में आंशिक न्यूनतम वर्ग निष्पादित करने का सबसे आसान तरीका pls पैकेज में फ़ंक्शंस का उपयोग करना है।

 #install pls package (if not already installed)
install.packages(" pls ")

load pls package
library(pls)

चरण 2: आंशिक न्यूनतम वर्ग मॉडल फिट करें

इस उदाहरण के लिए, हम एमटीकार्स नामक अंतर्निहित आर डेटासेट का उपयोग करेंगे जिसमें विभिन्न प्रकार की कारों पर डेटा शामिल है:

 #view first six rows of mtcars dataset
head(mtcars)

                   mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1

इस उदाहरण के लिए, हम एचपी को प्रतिक्रिया चर के रूप में और निम्नलिखित चर को भविष्यवक्ता चर के रूप में उपयोग करके आंशिक न्यूनतम वर्ग (पीएलएस) मॉडल फिट करेंगे:

• एमपीजी
• प्रदर्शन
• मल
• वज़न
• क्यूसेक

निम्नलिखित कोड दिखाता है कि पीएलएस मॉडल को इस डेटा में कैसे फिट किया जाए। निम्नलिखित तर्कों पर ध्यान दें:

• स्केल = सत्य : यह आर को बताता है कि डेटासेट में प्रत्येक चर को 0 के माध्य और 1 के मानक विचलन के लिए स्केल किया जाना चाहिए। यह सुनिश्चित करता है कि विभिन्न इकाइयों में मापा जाने पर किसी भी भविष्यवक्ता चर का मॉडल में बहुत अधिक प्रभाव नहीं पड़ता है।
• सत्यापन = “सीवी” : यह आर को मॉडल प्रदर्शन का मूल्यांकन करने के लिए के-फोल्ड क्रॉस सत्यापन का उपयोग करने के लिए कहता है। ध्यान दें कि यह डिफ़ॉल्ट रूप से k=10 फ़ोल्ड का उपयोग करता है। यह भी ध्यान दें कि लीव-वन-आउट क्रॉस-वैलिडेशन करने के लिए आप इसके बजाय “LOOCV” निर्दिष्ट कर सकते हैं।

 #make this example reproducible
set.seed(1)

#fit PCR model
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale= TRUE , validation=" CV ")

चरण 3: पीएलएस घटकों की संख्या चुनें

एक बार जब हम मॉडल फिट कर लेते हैं, तो हमें यह निर्धारित करने की आवश्यकता होती है कि कितने पीएलएस घटक रखने हैं।

ऐसा करने के लिए, बस के-क्रॉस सत्यापन द्वारा गणना की गई परीक्षण रूट माध्य वर्ग त्रुटि (परीक्षण आरएमएसई) को देखें:

 #view summary of model fitting
summary(model)

Data: 
	Y dimension: 32 1
Fit method: kernelpls
Number of components considered: 5

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept) 1 comp 2 comps 3 comps 4 comps 5 comps
CV 69.66 40.57 35.48 36.22 36.74 36.67
adjCV 69.66 40.41 35.12 35.80 36.27 36.20

TRAINING: % variance explained
    1 comp 2 comps 3 comps 4 comps 5 comps
X 68.66 89.27 95.82 97.94 100.00
hp 71.84 81.74 82.00 82.02 82.03

परिणाम में दो दिलचस्प तालिकाएँ हैं:

1. सत्यापन: आरएमएसईपी

यह तालिका हमें के-फोल्ड क्रॉस सत्यापन द्वारा गणना की गई आरएमएसई परीक्षण बताती है। हम निम्नलिखित देख सकते हैं:

• यदि हम मॉडल में केवल मूल शब्द का उपयोग करते हैं, तो परीक्षण का आरएमएसई 69.66 है।
• यदि हम पहला पीएलएस घटक जोड़ते हैं, तो आरएमएसई परीक्षण 40.57 तक गिर जाता है।
• यदि हम दूसरा पीएलएस घटक जोड़ते हैं, तो आरएमएसई परीक्षण घटकर 35.48 हो जाता है।

हम देख सकते हैं कि अतिरिक्त पीएलएस घटकों को जोड़ने से वास्तव में परीक्षण के आरएमएसई में वृद्धि होती है। इस प्रकार, ऐसा प्रतीत होता है कि अंतिम मॉडल में केवल दो पीएलएस घटकों का उपयोग करना इष्टतम होगा।

2. प्रशिक्षण: विचरण का % समझाया गया

यह तालिका हमें पीएलएस घटकों द्वारा समझाए गए प्रतिक्रिया चर में भिन्नता का प्रतिशत बताती है। हम निम्नलिखित देख सकते हैं:

• केवल पहले पीएलएस घटक का उपयोग करके, हम प्रतिक्रिया चर में 68.66% भिन्नता की व्याख्या कर सकते हैं।
• दूसरे पीएलएस घटक को जोड़कर, हम प्रतिक्रिया चर में 89.27% भिन्नता की व्याख्या कर सकते हैं।

ध्यान दें कि हम अभी भी अधिक पीएलएस घटकों का उपयोग करके अधिक विचरण की व्याख्या करने में सक्षम होंगे, लेकिन हम देख सकते हैं कि दो से अधिक पीएलएस घटकों को जोड़ने से वास्तव में विचरण के प्रतिशत में बहुत अधिक वृद्धि नहीं होती है।

हम वैलिडेशनप्लॉट() फ़ंक्शन का उपयोग करके पीएलएस घटकों की संख्या के एक फ़ंक्शन के रूप में आरएमएसई परीक्षण (एमएसई और आर-स्क्वायर टेस्ट के साथ) की भी कल्पना कर सकते हैं।

 #visualize cross-validation plots
validationplot(model)
validationplot(model, val.type=" MSEP ")
validationplot(model, val.type=" R2 ") 

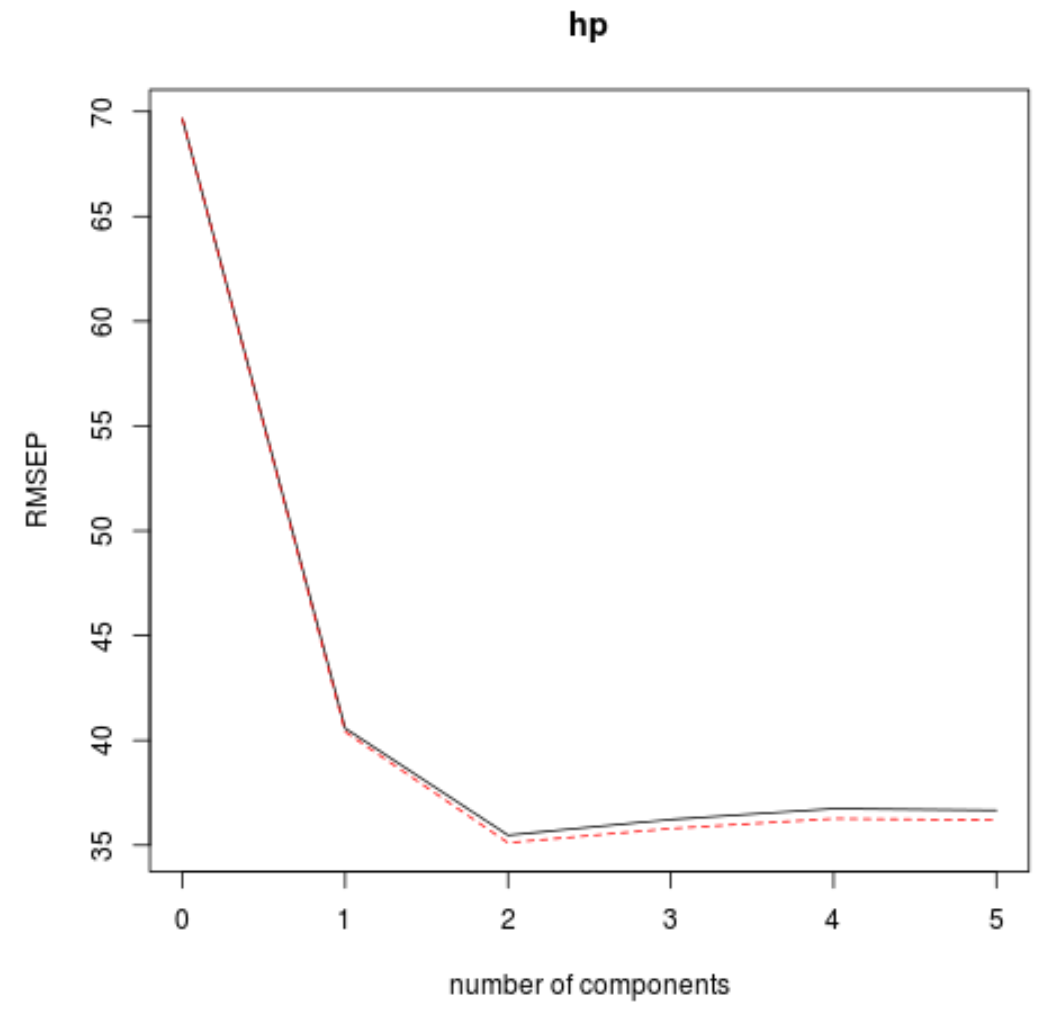
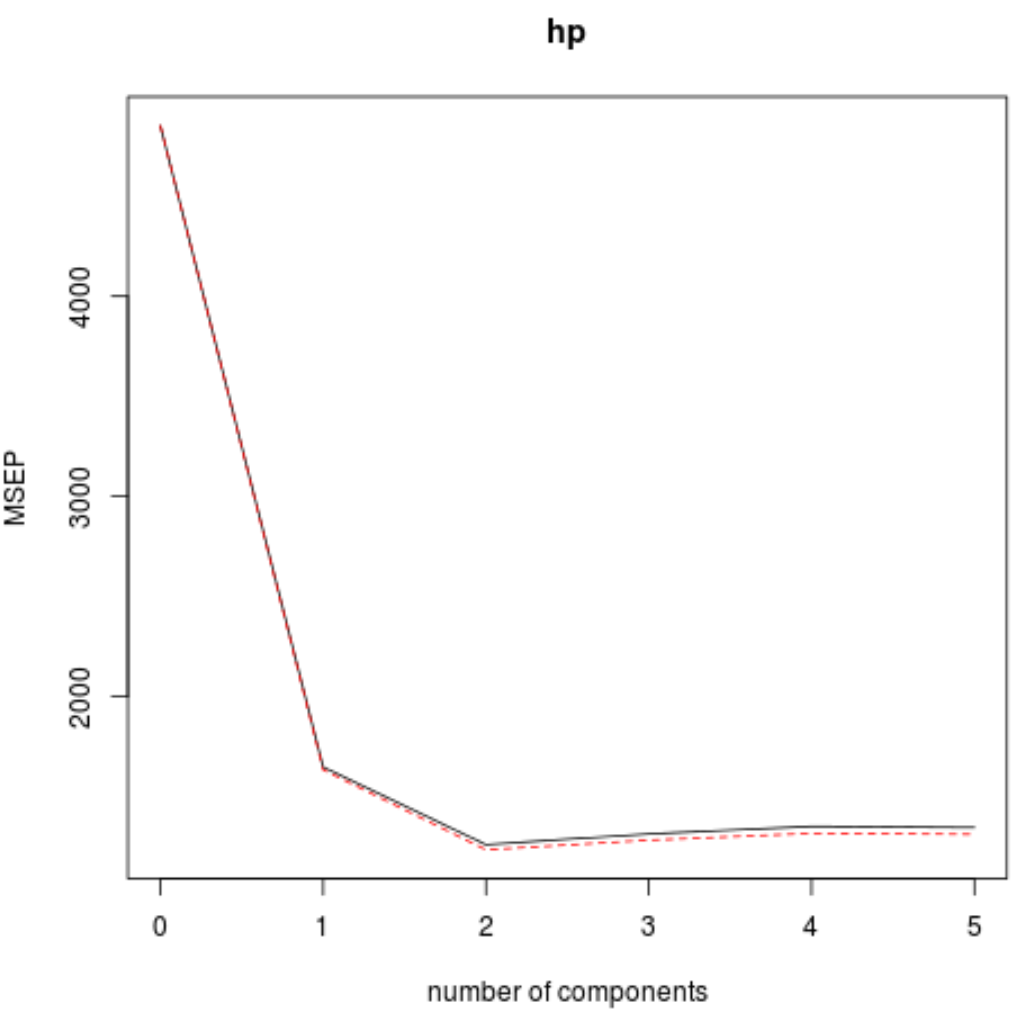
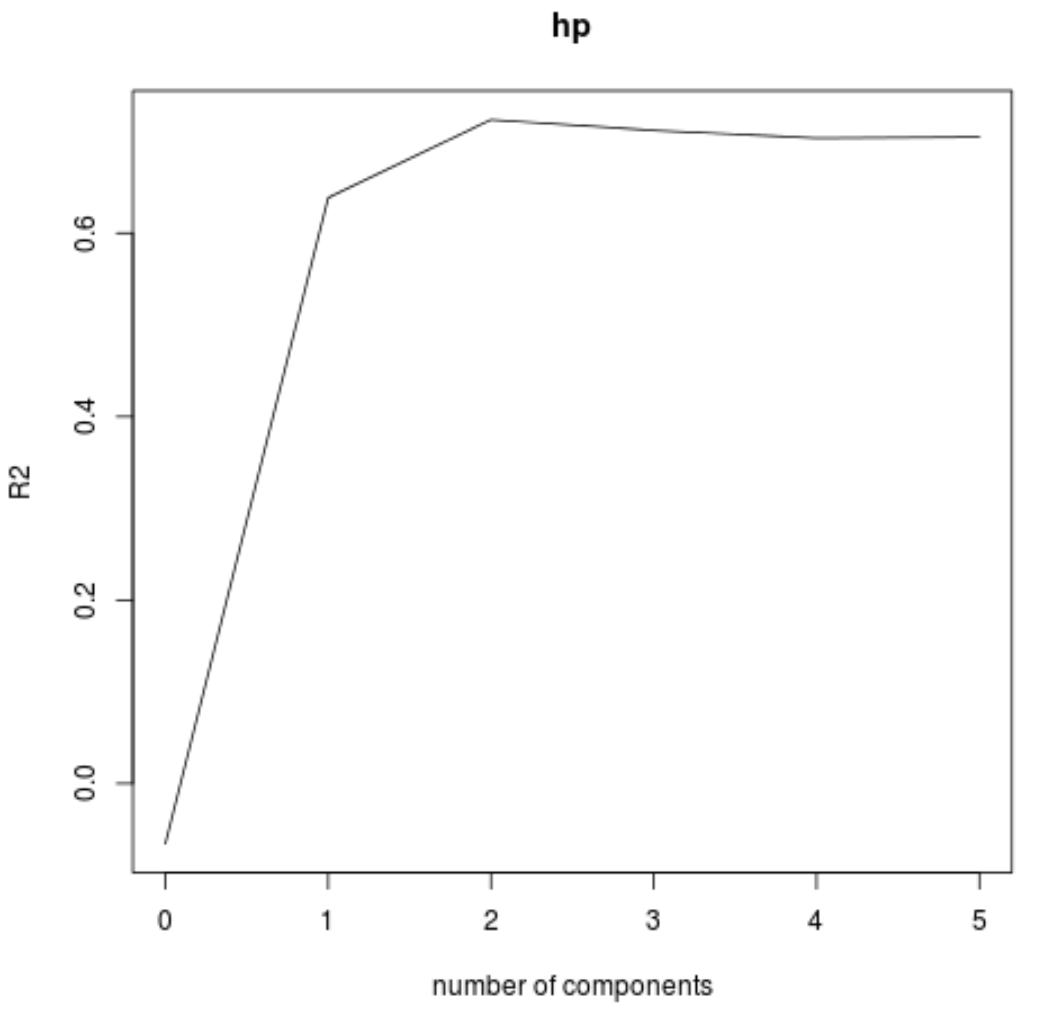
प्रत्येक ग्राफ़ में, हम देख सकते हैं कि दो पीएलएस घटकों को जोड़ने से मॉडल फिट में सुधार होता है, लेकिन जब हम अधिक पीएलएस घटकों को जोड़ते हैं तो यह खराब हो जाता है।

इस प्रकार, इष्टतम मॉडल में केवल पहले दो पीएलएस घटक शामिल हैं।

चरण 4: पूर्वानुमान लगाने के लिए अंतिम मॉडल का उपयोग करें

हम नए अवलोकनों के बारे में पूर्वानुमान लगाने के लिए दो पीएलएस घटकों के साथ अंतिम मॉडल का उपयोग कर सकते हैं।

निम्नलिखित कोड दिखाता है कि मूल डेटासेट को प्रशिक्षण और परीक्षण सेट में कैसे विभाजित किया जाए और परीक्षण सेट पर भविष्यवाणियां करने के लिए दो पीएलएस घटकों के साथ अंतिम मॉडल का उपयोग किया जाए।

 #define training and testing sets
train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")]
y_test <- mtcars[26: nrow (mtcars), c("hp")]
test <- mtcars[26: nrow (mtcars), c("mpg", "disp", "drat", "wt", "qsec")]
    
#use model to make predictions on a test set
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=train, scale= TRUE , validation=" CV ")
pcr_pred <- predict(model, test, ncomp= 2 )

#calculate RMSE
sqrt ( mean ((pcr_pred - y_test)^2))

[1] 54.89609

हमने देखा कि परीक्षण का RMSE 54.89609 निकला। यह परीक्षण सेट अवलोकनों के लिए अनुमानित एचपी मान और देखे गए एचपी मान के बीच औसत विचलन है।

ध्यान दें कि दो प्रमुख घटकों के साथ एक समतुल्य प्रमुख घटक प्रतिगमन मॉडल ने 56.86549 का एक परीक्षण आरएमएसई उत्पन्न किया। इस प्रकार, पीएलएस मॉडल ने इस डेटासेट के लिए पीसीआर मॉडल से थोड़ा बेहतर प्रदर्शन किया।

इस उदाहरण में आर कोड का पूरा उपयोग यहां पाया जा सकता है।