आर में नमूना वितरण की गणना कैसे करें
एक नमूना वितरण एक एकल आबादी से कई यादृच्छिक नमूनों के आधार पर एक निश्चित आंकड़े का संभाव्यता वितरण है।
यह ट्यूटोरियल बताता है कि आर में नमूना वितरण के साथ निम्नलिखित कैसे करें:
- एक नमूना वितरण उत्पन्न करें.
- नमूना वितरण की कल्पना करें.
- नमूना वितरण के माध्य और मानक विचलन की गणना करें।
- नमूना वितरण के संबंध में संभावनाओं की गणना करें।
आर में एक नमूना वितरण उत्पन्न करें
निम्नलिखित कोड दिखाता है कि आर में नमूना वितरण कैसे उत्पन्न किया जाए:
#make this example reproducible
set.seed(0)
#define number of samples
n = 10000
#create empty vector of length n
sample_means = rep (NA, n)
#fill empty vector with means
for (i in 1:n){
sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}
#view first six sample means
head(sample_means)
[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656
इस उदाहरण में, हमने 10,000 नमूनों के औसत की गणना करने के लिए rnorm() फ़ंक्शन का उपयोग किया, जिसमें प्रत्येक नमूना आकार 20 था और 5.3 के माध्य और 9 के मानक विचलन के साथ सामान्य वितरण से उत्पन्न हुआ था।
हम देख सकते हैं कि पहले नमूने का माध्य 5.283992 था, दूसरे नमूने का माध्य 6.304845 था, इत्यादि।
नमूना वितरण की कल्पना करें
निम्नलिखित कोड दिखाता है कि नमूना वितरण को देखने के लिए एक सरल हिस्टोग्राम कैसे बनाया जाए:
#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")
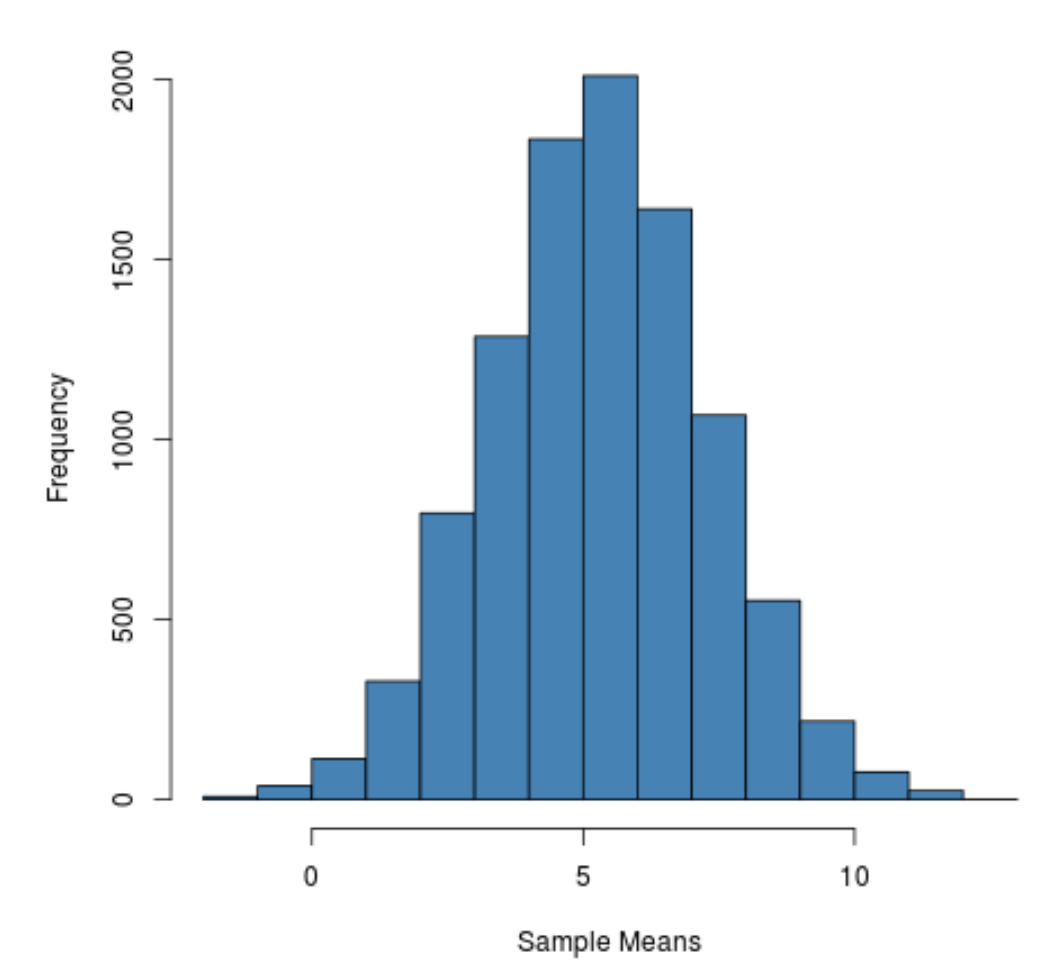
यह देखा जा सकता है कि नमूना वितरण घंटी के आकार का है जिसका शिखर मान 5 के करीब है।
हालाँकि, वितरण के विवरण से हम देख सकते हैं कि कुछ नमूनों का मतलब 10 से अधिक था और अन्य का मतलब 0 से कम था।
माध्य और मानक विचलन ज्ञात कीजिए
निम्नलिखित कोड दिखाता है कि नमूना वितरण के माध्य और मानक विचलन की गणना कैसे करें:
#mean of sampling distribution
mean(sample_means)
[1] 5.287195
#standard deviation of sampling distribution
sd(sample_means)
[1] 2.00224
सैद्धांतिक रूप से, नमूना वितरण का माध्य 5.3 होना चाहिए। हम देख सकते हैं कि इस उदाहरण में वास्तविक नमूना माध्य 5.287195 है, जो 5.3 के करीब है।
और सैद्धांतिक रूप से, नमूना वितरण का मानक विचलन s/√n के बराबर होना चाहिए, जो 9 / √20 = 2.012 होगा। हम देख सकते हैं कि नमूना वितरण का वास्तविक मानक विचलन 2.00224 है, जो 2.012 के करीब है।
संभावनाओं की गणना करें
निम्नलिखित कोड दिखाता है कि जनसंख्या माध्य, जनसंख्या मानक विचलन और नमूना आकार को देखते हुए नमूना माध्य के लिए एक निश्चित मूल्य प्राप्त करने की संभावना की गणना कैसे की जाए।
#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)
इस विशेष उदाहरण में, हम संभावना पाते हैं कि नमूना माध्य 6 से कम या उसके बराबर है, यह देखते हुए कि जनसंख्या माध्य 5.3 है, जनसंख्या मानक विचलन 9 है, और 20 के नमूने का आकार 0.6417 है।
यह नमूनाकरण वितरण कैलकुलेटर द्वारा गणना की गई संभावना के बहुत करीब है:

पूरा कोड
इस उदाहरण में प्रयुक्त संपूर्ण R कोड नीचे दिखाया गया है:
#make this example reproducible
set.seed(0)
#define number of samples
n = 10000
#create empty vector of length n
sample_means = rep (NA, n)
#fill empty vector with means
for (i in 1:n){
sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}
#view first six sample means
head(sample_means)
#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")
#mean of sampling distribution
mean(sample_means)
#standard deviation of sampling distribution
sd(sample_means)
#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)
अतिरिक्त संसाधन
नमूना वितरण का एक परिचय
नमूना वितरण कैलकुलेटर
केंद्रीय सीमा प्रमेय का एक परिचय