आर में भारित न्यूनतम वर्ग प्रतिगमन कैसे करें

रैखिक प्रतिगमन की प्रमुख धारणाओं में से एक यह है कि अवशिष्टों को भविष्यवक्ता चर के प्रत्येक स्तर पर समान भिन्नता के साथ वितरित किया जाता है। इस धारणा को समरूपता के रूप में जाना जाता है।

जब इस धारणा का सम्मान नहीं किया जाता है, तो कहा जाता है कि अवशेषों में विषमलैंगिकता मौजूद है। जब ऐसा होता है, तो प्रतिगमन परिणाम अविश्वसनीय हो जाते हैं।

इस समस्या को हल करने का एक तरीका भारित न्यूनतम वर्ग प्रतिगमन का उपयोग करना है, जो अवलोकनों को वजन प्रदान करता है जैसे कि कम त्रुटि भिन्नता वाले लोगों को अधिक वजन मिलता है क्योंकि उनमें अधिक त्रुटि भिन्नता वाले अवलोकनों की तुलना में अधिक जानकारी होती है।

यह ट्यूटोरियल चरण-दर-चरण उदाहरण प्रदान करता है कि आर में भारित न्यूनतम वर्ग प्रतिगमन कैसे करें।

चरण 1: डेटा बनाएं

निम्नलिखित कोड एक डेटा फ़्रेम बनाता है जिसमें अध्ययन किए गए घंटों की संख्या और 16 छात्रों के लिए संबंधित परीक्षा स्कोर शामिल है:

 df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
                 score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))

चरण 2: रेखीय प्रतिगमन करें

इसके बाद, हम एक सरल रैखिक प्रतिगमन मॉडल को फिट करने के लिए एलएम() फ़ंक्शन का उपयोग करेंगे जो भविष्यवक्ता चर के रूप में घंटों का उपयोग करता है और प्रतिक्रिया चर के रूप में स्कोर का उपयोग करता है:

 #fit simple linear regression model
model <- lm(score ~ hours, data = df)

#view summary of model
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-17,967 -5,970 -0.719 7,531 15,032 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 60,467 5,128 11,791 1.17e-08 ***
hours 5,500 1,127 4,879 0.000244 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 9.224 on 14 degrees of freedom
Multiple R-squared: 0.6296, Adjusted R-squared: 0.6032 
F-statistic: 23.8 on 1 and 14 DF, p-value: 0.0002438

चरण 3: विषमलैंगिकता का परीक्षण करें

इसके बाद, हम विषमलैंगिकता की दृष्टि से जांच करने के लिए अवशेषों और फिट किए गए मूल्यों का एक प्लॉट बनाएंगे:

 #create residual vs. fitted plot
plot( fitted (model), resid (model), xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

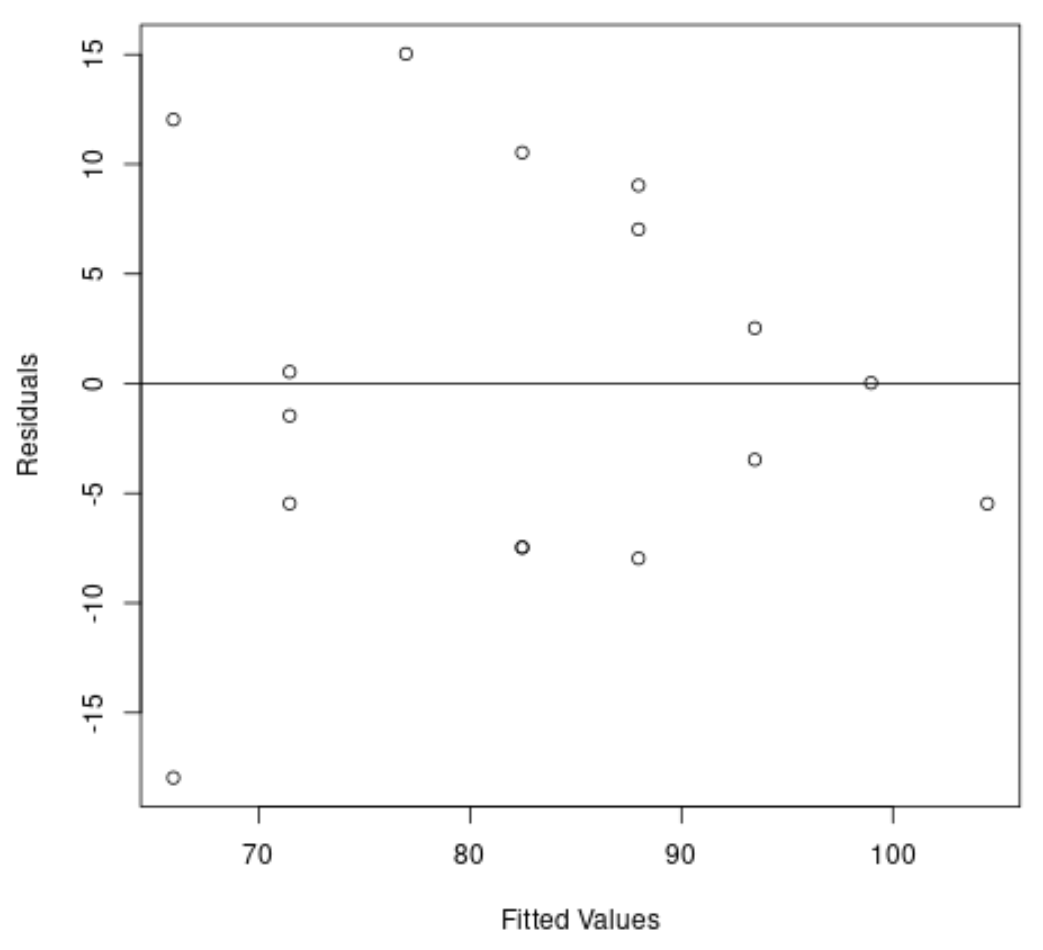
हम ग्राफ़ से देख सकते हैं कि अवशेषों का एक “शंकु” आकार है: वे पूरे ग्राफ़ में समान भिन्नता के साथ वितरित नहीं हैं।

औपचारिक रूप से विषमलैंगिकता का परीक्षण करने के लिए, हम ब्रूश-पैगन परीक्षण कर सकते हैं:

 #load lmtest package
library (lmtest)

#perform Breusch-Pagan test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 3.9597, df = 1, p-value = 0.0466

ब्रूश-पेगन परीक्षण निम्नलिखित शून्य और वैकल्पिक परिकल्पनाओं का उपयोग करता है:

• शून्य परिकल्पना (H ₀ ): समरूपता मौजूद है (अवशेषों को समान भिन्नता के साथ वितरित किया जाता है)
• वैकल्पिक परिकल्पना ( _एचए ): विषमलैंगिकता मौजूद है (अवशेषों को समान भिन्नता के साथ वितरित नहीं किया जाता है)

चूँकि परीक्षण का पी-मान 0.0466 है, हम शून्य परिकल्पना को अस्वीकार कर देंगे और निष्कर्ष निकालेंगे कि इस मॉडल में विषमलैंगिकता एक समस्या है।

चरण 4: भारित न्यूनतम वर्ग प्रतिगमन निष्पादित करें

चूँकि विषमलैंगिकता मौजूद है, हम वज़न निर्धारित करके कम से कम भार वाले वर्गों का प्रदर्शन करेंगे, ताकि कम विचरण वाले अवलोकनों को अधिक वजन प्राप्त हो:

 #define weights to use
wt <- 1 / lm( abs (model$residuals) ~ model$fitted. values )$fitted. values ^2

#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)

#view summary of model
summary(wls_model)

Call:
lm(formula = score ~ hours, data = df, weights = wt)

Weighted Residuals:
    Min 1Q Median 3Q Max 
-2.0167 -0.9263 -0.2589 0.9873 1.6977 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.9689 5.1587 12.400 6.13e-09 ***
hours 4.7091 0.8709 5.407 9.24e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared: 0.6762, Adjusted R-squared: 0.6531 
F-statistic: 29.24 on 1 and 14 DF, p-value: 9.236e-05

परिणामों से, हम देख सकते हैं कि घंटे भविष्यवक्ता चर के लिए गुणांक अनुमान थोड़ा बदल गया और समग्र मॉडल फिट में सुधार हुआ।

भारित न्यूनतम वर्ग मॉडल में मूल सरल रैखिक प्रतिगमन मॉडल में 9.224 की तुलना में 1.199 की अवशिष्ट मानक त्रुटि है।

यह इंगित करता है कि भारित न्यूनतम वर्ग मॉडल द्वारा उत्पादित अनुमानित मूल्य सरल रैखिक प्रतिगमन मॉडल द्वारा उत्पादित अनुमानित मूल्यों की तुलना में वास्तविक अवलोकनों के बहुत करीब हैं।

भारित न्यूनतम वर्ग मॉडल में भी 0.6762 का आर-वर्ग है, जबकि मूल सरल रैखिक प्रतिगमन मॉडल में 0.6296 है ।

यह इंगित करता है कि भारित न्यूनतम वर्ग मॉडल सरल रैखिक प्रतिगमन मॉडल की तुलना में परीक्षा अंकों में अधिक भिन्नता को समझाने में सक्षम है।

इन मापों से संकेत मिलता है कि भारित न्यूनतम वर्ग मॉडल सरल रैखिक प्रतिगमन मॉडल की तुलना में डेटा के लिए बेहतर फिट प्रदान करता है।

अतिरिक्त संसाधन

आर में सरल रैखिक प्रतिगमन कैसे करें
आर में मल्टीपल लीनियर रिग्रेशन कैसे करें
आर में क्वांटाइल रिग्रेशन कैसे करें