एक-मॉडल वितरण क्या है? (परिभाषा & #038; उदाहरण)

एक यूनिमॉडल वितरण एक स्पष्ट शिखर वाला संभाव्यता वितरण है।

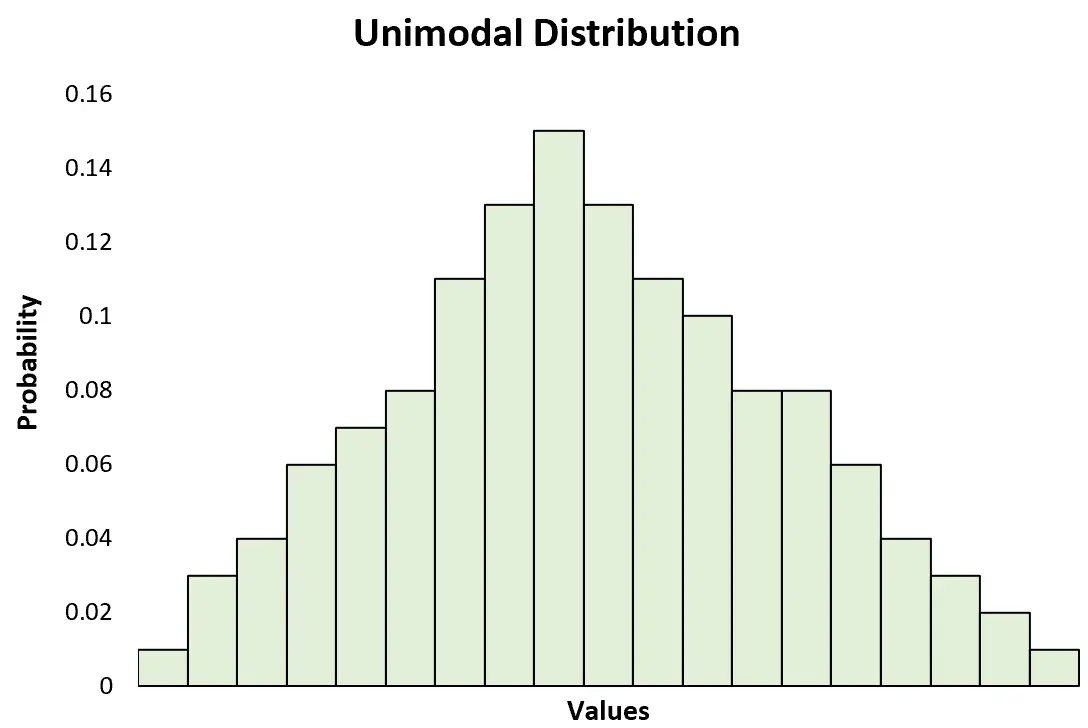
यह द्वि-मोडल वितरण के विपरीत है, जिसमें दो स्पष्ट शिखर हैं:

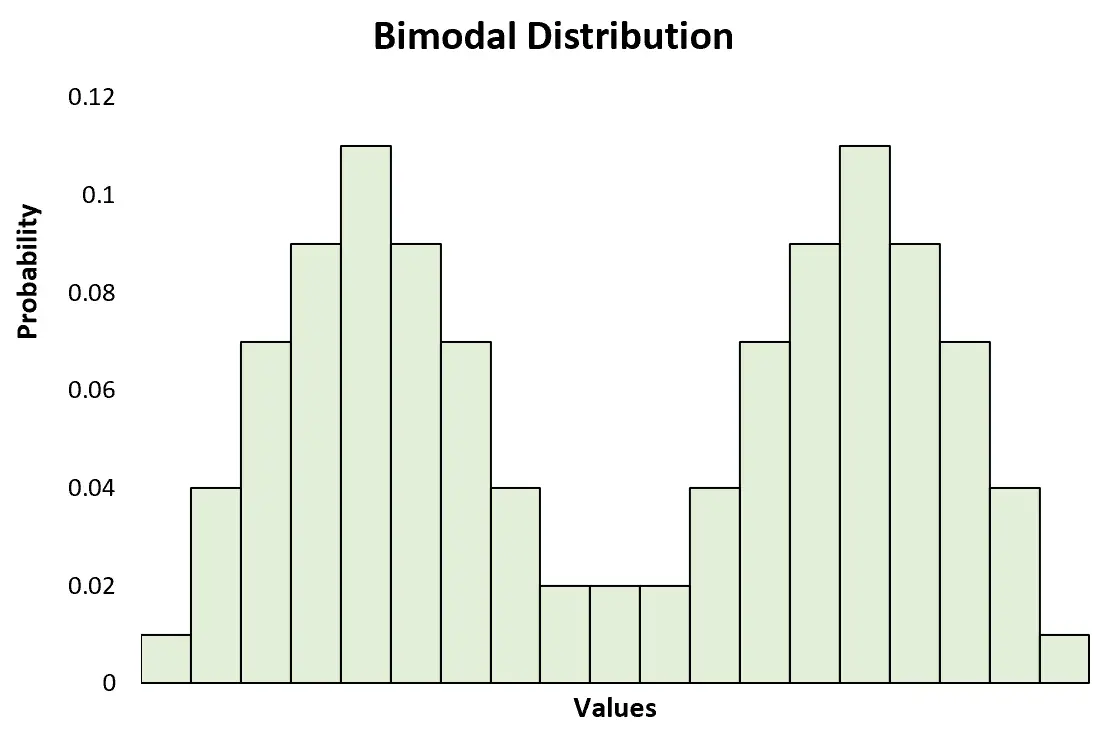
यह मल्टीमॉडल वितरण के भी विपरीत है, जिसमें दो या दो से अधिक शिखर हैं:

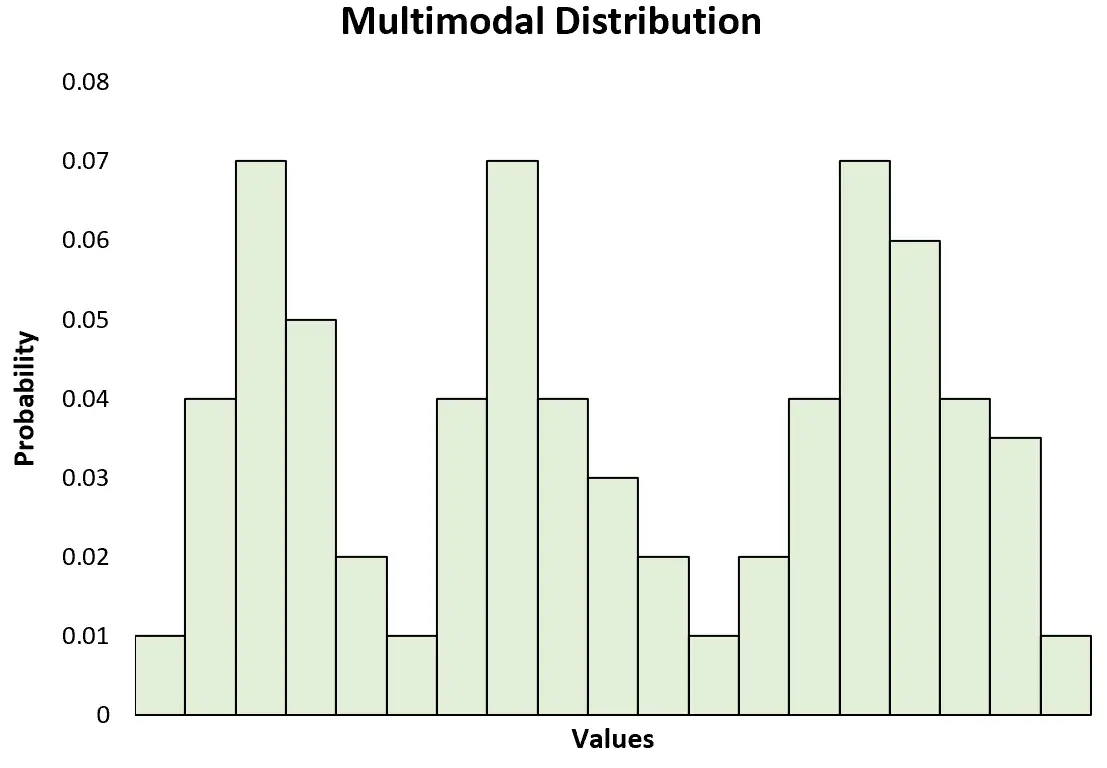
ध्यान दें: एक द्विमॉडल वितरण केवल एक विशिष्ट प्रकार का मल्टीमॉडल वितरण है।

एक-मॉडल वितरण के उदाहरण

व्यवहार में एकरूप वितरण के कुछ उदाहरण यहां दिए गए हैं।

उदाहरण 1: जन्म के समय शिशुओं का वजन

यह सर्वविदित है कि नवजात शिशुओं का वजन वितरण एक समान वितरण के अनुसार होता है, जिसका औसत लगभग 7.5 पाउंड होता है। यदि हम शिशुओं के वजन का एक हिस्टोग्राम बनाते हैं, तो हम 7.5 पाउंड पर “शिखर” देखेंगे, जिसमें कुछ शिशुओं का वजन अधिक होगा और अन्य का वजन कम होगा।

उदाहरण 2: ACT स्कोर

संयुक्त राज्य अमेरिका में हाई स्कूल के छात्रों के लिए औसत ACT स्कोर 21 के आसपास है, कुछ छात्रों ने कम अंक प्राप्त किए हैं और अन्य ने अधिक अंक प्राप्त किए हैं। यदि हम संयुक्त राज्य अमेरिका में सभी छात्रों के लिए एसीटी स्कोर का एक हिस्टोग्राम बनाते हैं, तो हम 21 साल की उम्र में एक एकल “शिखर” देखेंगे, जिसमें कुछ छात्रों के लिए उच्च स्कोर और अन्य के लिए कम स्कोर होंगे।

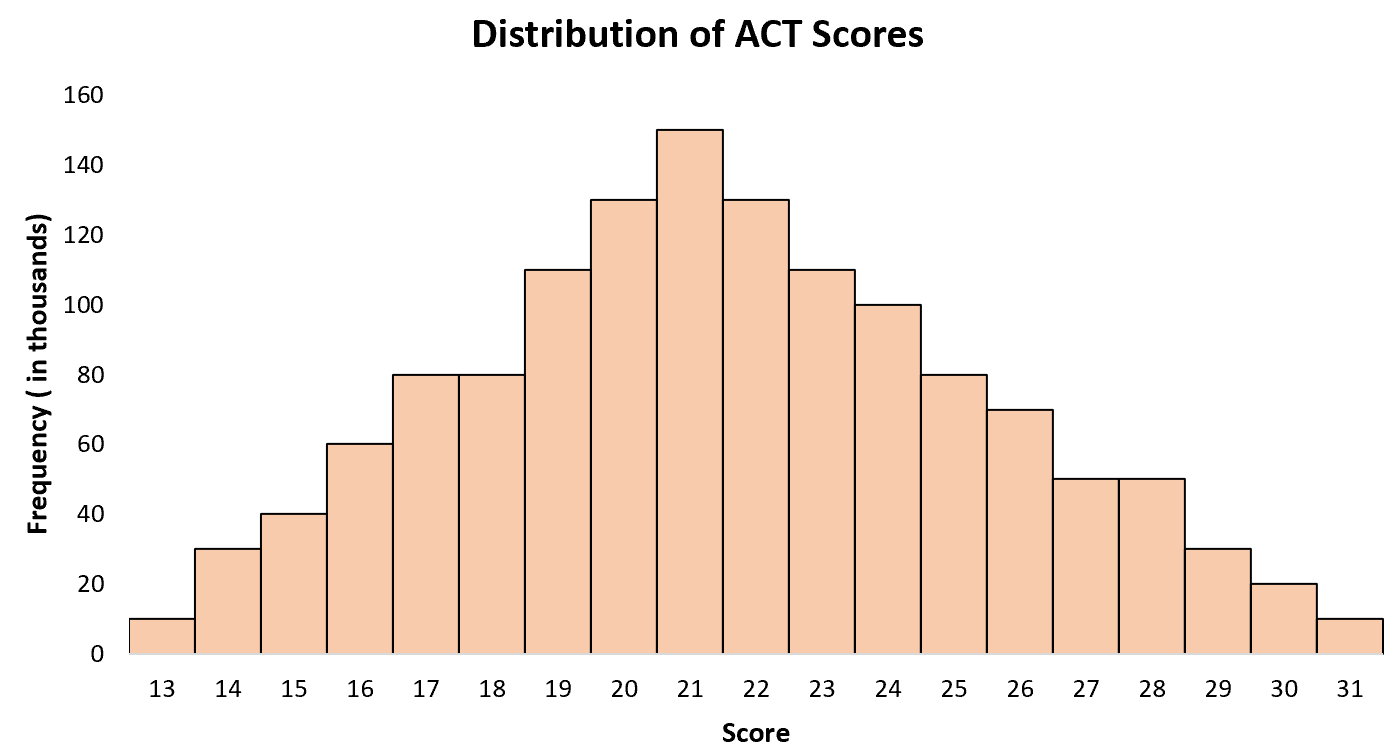
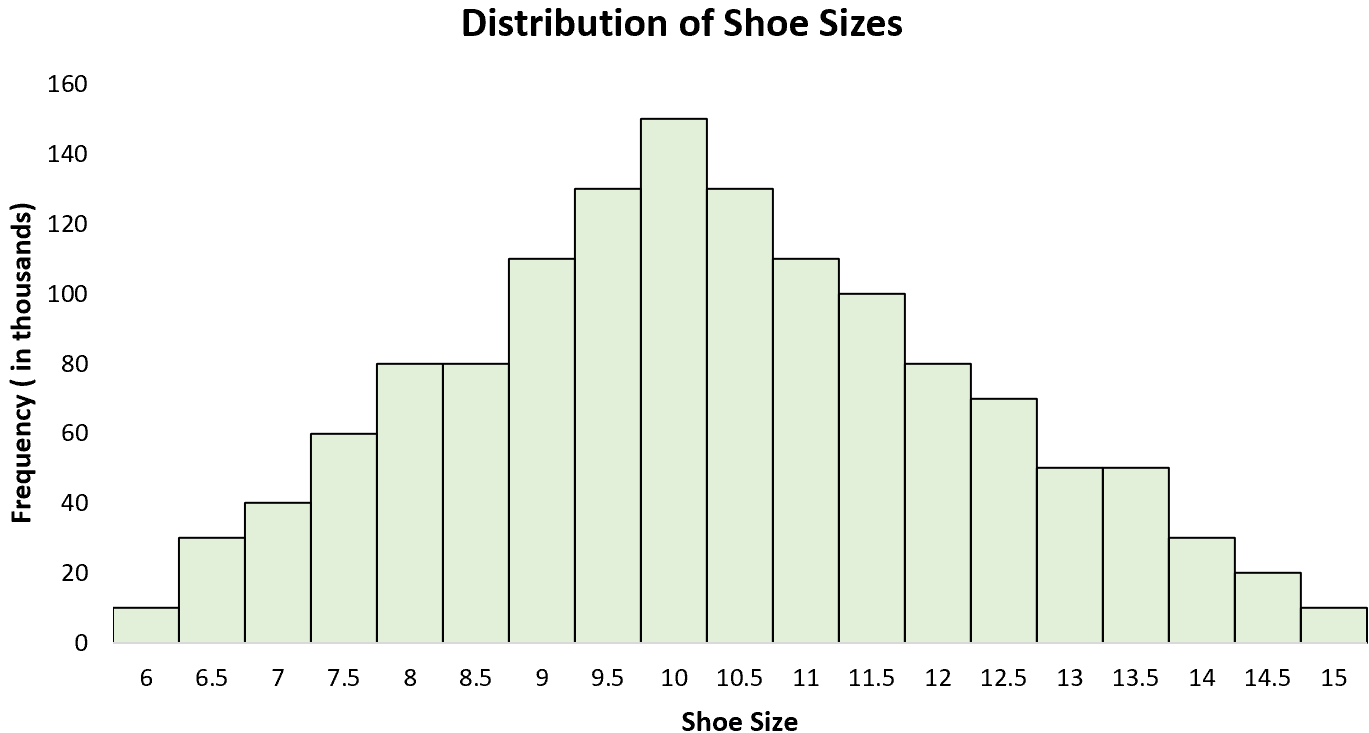
उदाहरण 3: जूते का आकार

पुरुषों के जूते के आकार का वितरण लगभग 10 के “शिखर” के साथ एक असमान वितरण है। यदि हम सभी पुरुषों के जूते के आकार का एक हिस्टोग्राम बनाते हैं, तो हम 10 पर एक एकल शिखर देखेंगे, जिसमें कुछ पुरुष बड़े आकार के जूते पहनते हैं और अन्य बड़े आकार के जूते पहनते हैं। आकार। छोटे आकार का।

सांख्यिकी में यूनिमॉडल वितरण

सांख्यिकी में निम्नलिखित संभाव्यता वितरण सभी एकरूप वितरण हैं:

सामान्य वितरण

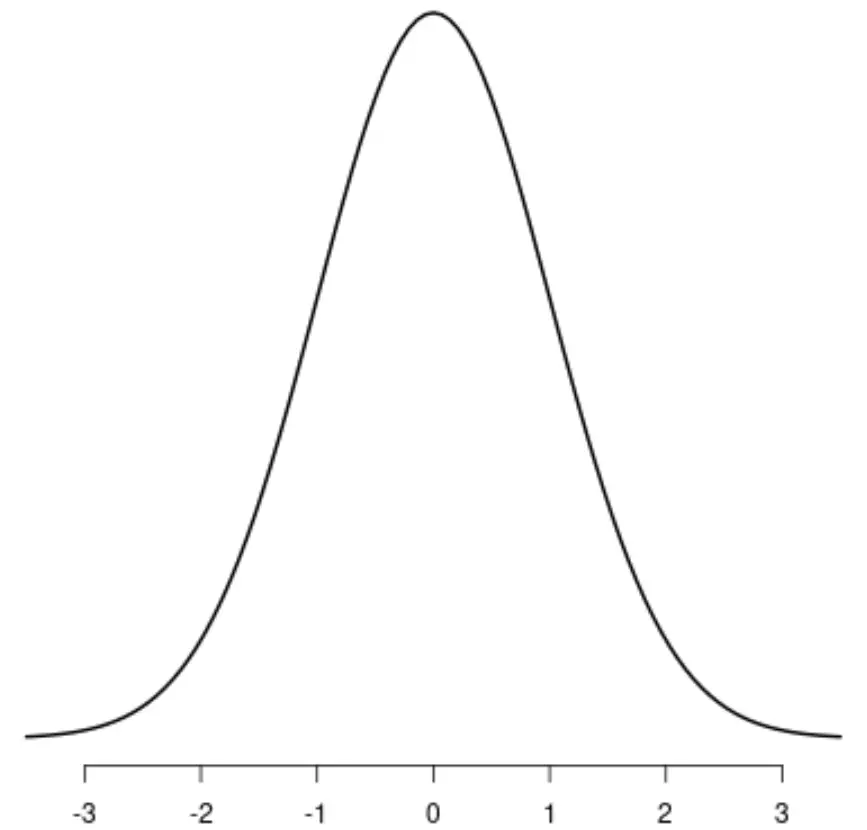
वितरण टी

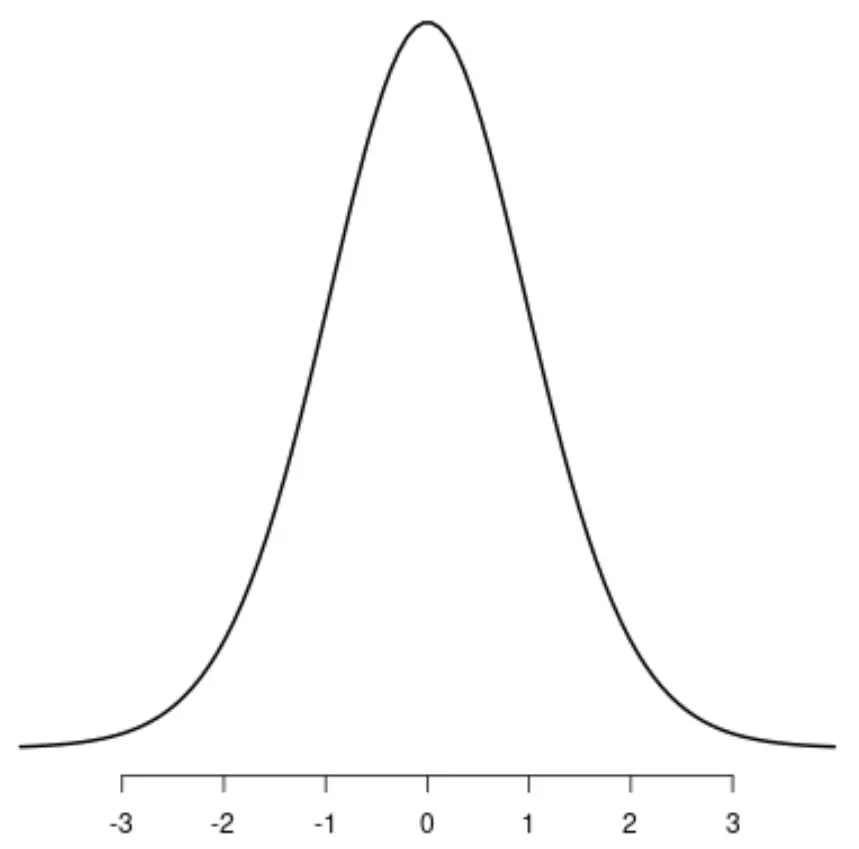
वर्दी वितरण

कॉची वितरण

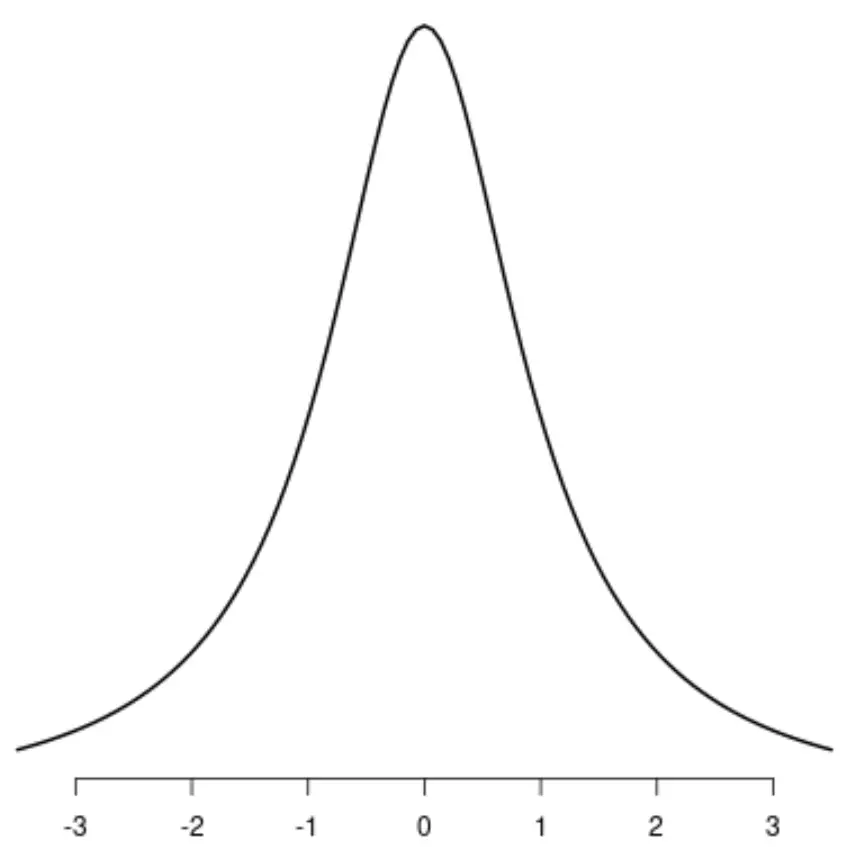
ध्यान दें कि इनमें से प्रत्येक वितरण का एक अलग शिखर है।

यूनिमॉडल वितरण का विश्लेषण कैसे करें

हम अक्सर केंद्रीय प्रवृत्ति के तीन अलग-अलग मापों का उपयोग करके एकरूप वितरण का वर्णन करते हैं:

• औसत : औसत मूल्य
• माध्यिका : माध्यिका मान
• मोड : वह मान जो सबसे अधिक बार दिखाई देता है

वितरण की विषमता के आधार पर, ये तीन माप अलग-अलग स्थानों पर पाए जा सकते हैं।

बाएँ-तिरछा वितरण: माध्य <मध्यिका <मोड

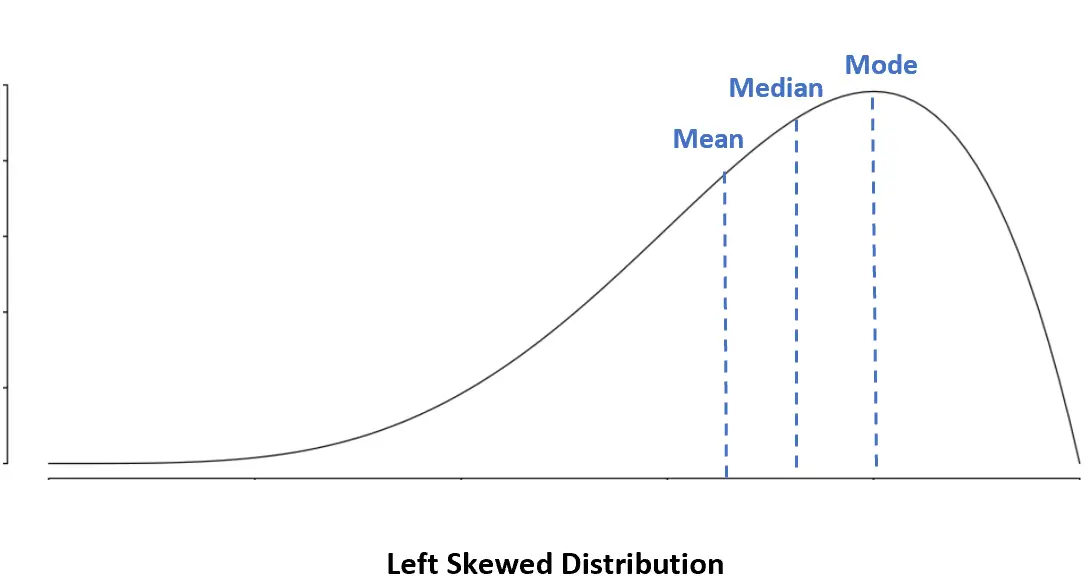
बाएँ-तिरछे वितरण में, माध्य माध्यिका से कम होता है।

दाएं-तिरछा वितरण: मोड < माध्य < माध्य

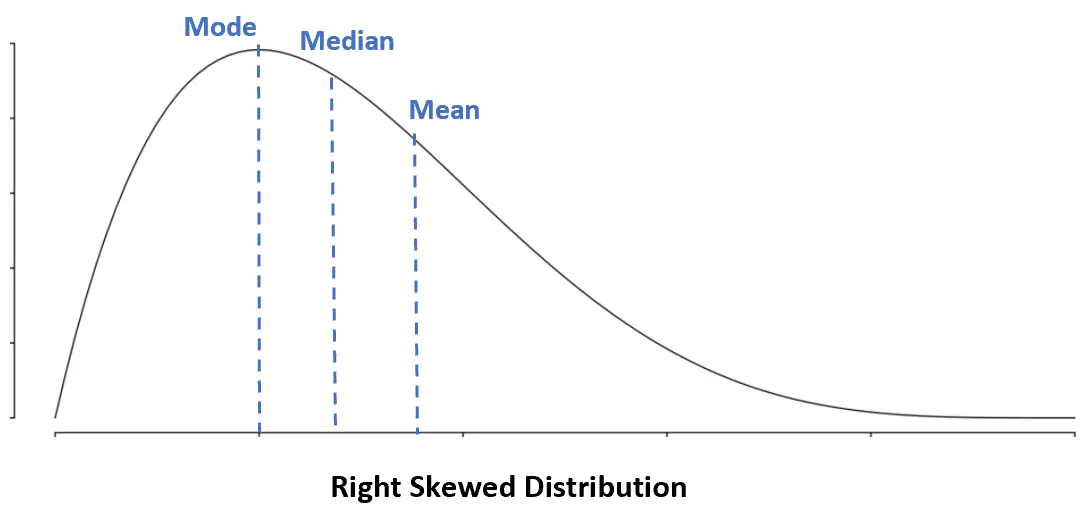
दाएं-तिरछे वितरण में, माध्य माध्यिका से अधिक होता है।

कोई पूर्वाग्रह नहीं: माध्य = माध्यिका = बहुलक

एक सममित वितरण में, माध्य, माध्यिका और बहुलक सभी समान होते हैं।

अतिरिक्त संसाधन

बाएँ या दाएँ तिरछा वितरण
सममित वितरण: परिभाषा + उदाहरण