आर में घातीय प्रतिगमन (चरण दर चरण)

घातीय प्रतिगमन एक प्रकार का प्रतिगमन है जिसका उपयोग निम्नलिखित स्थितियों को मॉडल करने के लिए किया जा सकता है:

1. घातीय वृद्धि: विकास धीरे-धीरे शुरू होता है और फिर तेजी से और बिना किसी सीमा के तेज हो जाता है।

2. घातीय क्षय: क्षय तेजी से शुरू होता है और फिर धीमा होकर शून्य के करीब पहुंच जाता है।

घातीय प्रतिगमन मॉडल के लिए समीकरण निम्नलिखित रूप लेता है:

y = एबी ^एक्स

सोना:

• y: प्रतिक्रिया चर
• x: पूर्वानुमानित चर
• ए, बी: प्रतिगमन गुणांक जो एक्स और वाई के बीच संबंध का वर्णन करते हैं

निम्नलिखित चरण-दर-चरण उदाहरण दिखाता है कि आर में घातीय प्रतिगमन कैसे करें।

चरण 1: डेटा बनाएं

सबसे पहले, आइए दो वेरिएबल्स के लिए नकली डेटा बनाएं: x और y :

 x=1:20
y=c(1, 3, 5, 7, 9, 12, 15, 19, 23, 28, 33, 38, 44, 50, 56, 64, 73, 84, 97, 113)

चरण 2: डेटा को विज़ुअलाइज़ करें

इसके बाद, आइए x और y के बीच संबंध को देखने के लिए एक त्वरित स्कैटरप्लॉट बनाएं:

 plot(x, y) 

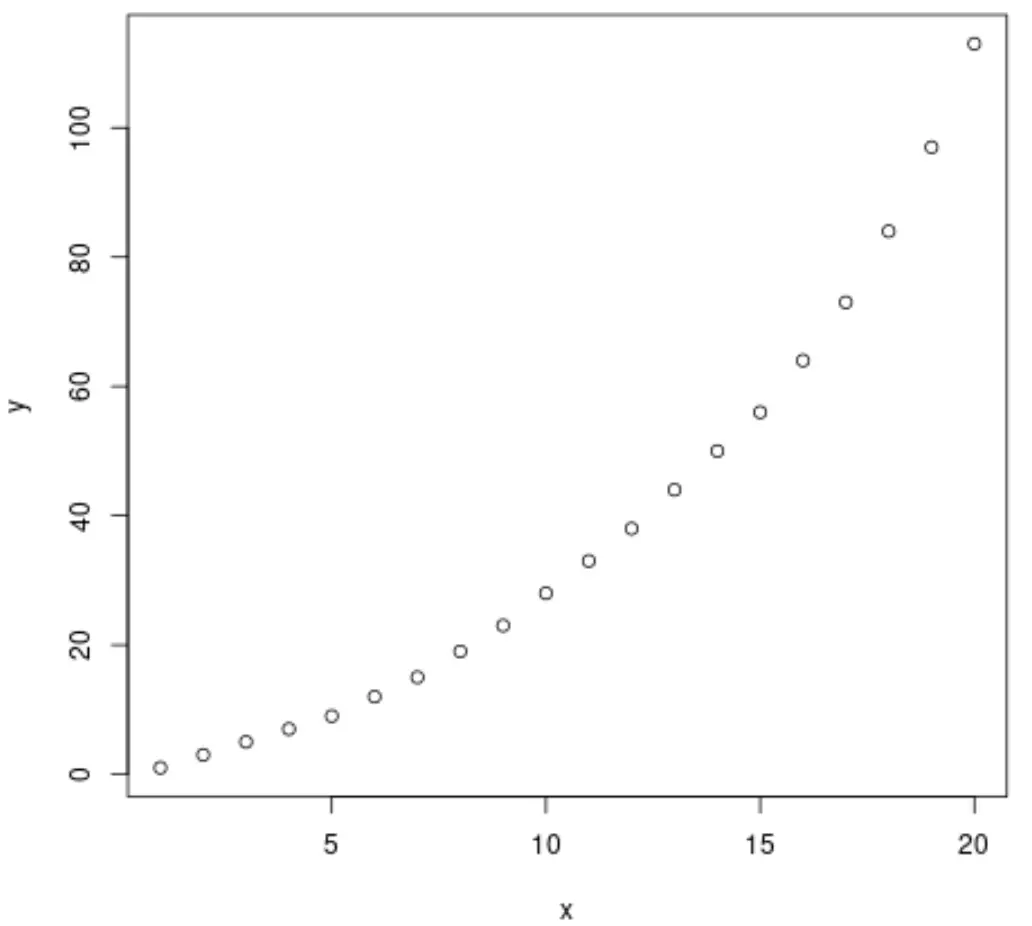
ग्राफ़ से, हम देख सकते हैं कि दो चरों के बीच एक स्पष्ट घातीय वृद्धि पैटर्न है।

इसलिए चरों के बीच संबंध का वर्णन करने के लिए एक घातीय प्रतिगमन समीकरण को फिट करना बुद्धिमानी लगता है।

चरण 3: घातीय प्रतिगमन मॉडल को फ़िट करें

इसके बाद, हम प्रतिक्रिया चर के रूप में y के प्राकृतिक लघुगणक और भविष्यवक्ता चर के रूप में x का उपयोग करके एक घातीय प्रतिगमन मॉडल को फिट करने के लिए lm() फ़ंक्शन का उपयोग करेंगे:

 #fit the model
model <- lm( log (y) ~ x)

#view the output of the model
summary(model)

Call:
lm(formula = log(y) ~ x)

Residuals:
    Min 1Q Median 3Q Max 
-1.1858 -0.1768 0.1104 0.2720 0.3300 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.98166 0.17118 5.735 1.95e-05 ***
x 0.20410 0.01429 14.283 2.92e-11 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3685 on 18 degrees of freedom
Multiple R-squared: 0.9189, Adjusted R-squared: 0.9144 
F-statistic: 204 on 1 and 18 DF, p-value: 2.917e-11

मॉडल का समग्र एफ-वैल्यू 204 है और संबंधित पी-वैल्यू बेहद कम (2.917ई-11) है, जो दर्शाता है कि मॉडल समग्र रूप से उपयोगी है।

आउटपुट तालिका से गुणांकों का उपयोग करके, हम देख सकते हैं कि फिट किया गया घातीय प्रतिगमन समीकरण है:

एलएन(वाई) = 0.9817 + 0.2041(एक्स)

दोनों पक्षों पर ई लागू करके, हम समीकरण को इस प्रकार फिर से लिख सकते हैं:

y = 2.6689 * ^1.2264x

हम इस समीकरण का उपयोग भविष्यवक्ता चर, x के मान के आधार पर, प्रतिक्रिया चर, y की भविष्यवाणी करने के लिए कर सकते हैं। उदाहरण के लिए, यदि x = 12, तो हम अनुमान लगाएंगे कि y 30.897 होगा:

y = 2.6689 * 1.2264 ¹² = 30.897

बोनस: किसी दिए गए भविष्यवक्ता और प्रतिक्रिया चर के लिए घातीय प्रतिगमन समीकरण की स्वचालित रूप से गणना करने के लिए इस ऑनलाइन घातीय प्रतिगमन कैलकुलेटर का उपयोग करने में संकोच न करें।

अतिरिक्त संसाधन

आर में सरल रैखिक प्रतिगमन कैसे करें
आर में मल्टीपल लीनियर रिग्रेशन कैसे करें
आर में द्विघात प्रतिगमन कैसे करें
आर में बहुपद प्रतिगमन कैसे करें