वृक्षारेख

यह आलेख बताता है कि वृक्ष आरेख क्या है और इसे कैसे बनाया जाता है। इस प्रकार, आपको वृक्ष संरचनाओं के उदाहरण, इस प्रकार के आरेख के फायदे और, इसके अलावा, चरण दर चरण हल किया गया एक अभ्यास मिलेगा।

वृक्ष क्या हैं?

एक वृक्ष आरेख , जिसे संभाव्यता वृक्ष भी कहा जाता है, एक प्रयोग के सभी संभावित परिणामों का उनकी संभावनाओं के साथ एक चित्रमय प्रतिनिधित्व है।

इस प्रकार, एक नमूना स्थान में सभी संभावित परिणामों को रेखांकन करने और उनकी संभावनाओं की गणना करने के लिए एक वृक्ष आरेख का उपयोग किया जाता है।

एक वृक्ष आरेख इस प्रकार बनाया जाता है कि अंतिम परिणाम तक पहुंचने तक प्रत्येक परिणाम ( नोड ) नए संभावित परिणामों ( शाखाओं ) में बदल जाता है।

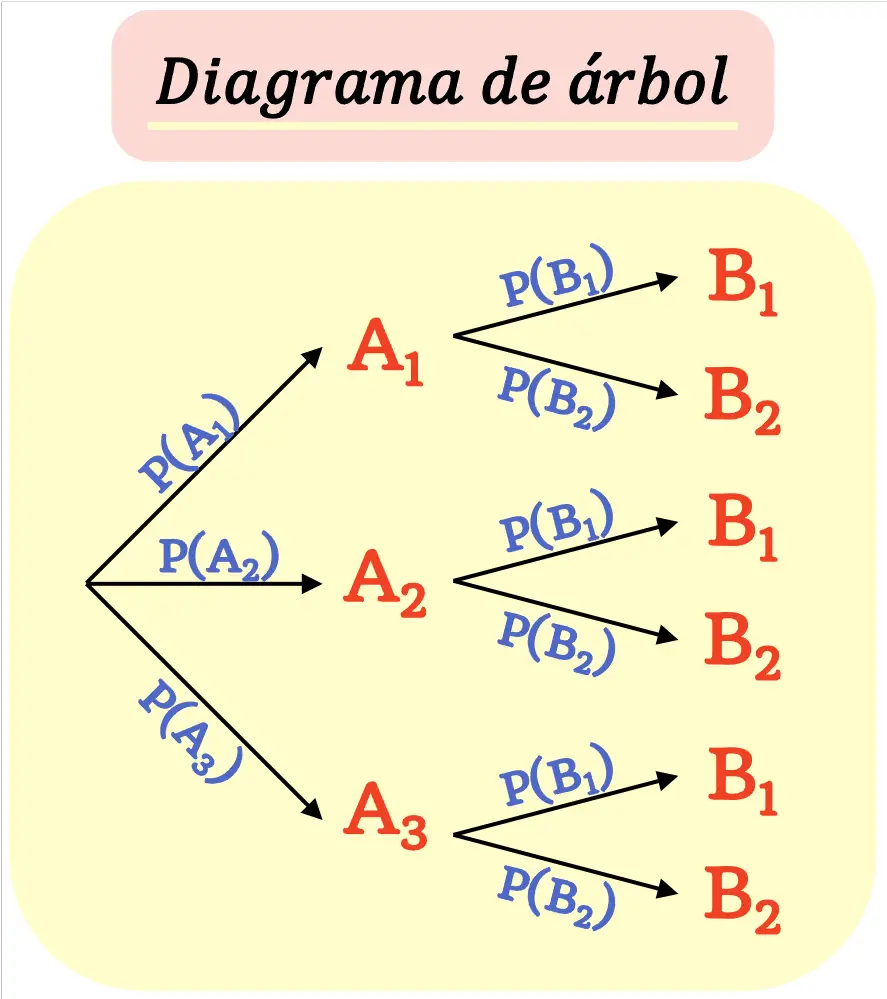
यह ध्यान में रखना चाहिए कि एक नोड से निकलने वाली सभी शाखाओं की संभावनाओं का योग 1 के बराबर होना चाहिए।

वृक्ष आरेख कैसे बनाएं

एक पेड़ बनाने के लिए, आपको निम्नलिखित चरणों का पालन करना होगा:

1. वृक्ष आरेख बनाने में पहला कदम प्रत्येक संभावित परिणाम के लिए एक शाखा बनाना है। ये पहली पीढ़ी की शाखाएँ होंगी।
2. फिर, प्रत्येक घटना से जुड़ी संभावना को उसकी संबंधित शाखा में जोड़ा जाता है।
3. प्रत्येक पहली पीढ़ी की शाखा का अंत एक नोड है जिससे बाद की संभावित घटनाओं की शाखाओं का प्रतिनिधित्व किया जाना चाहिए।
4. पहली शाखाओं की तरह, हमें प्रस्तुत घटनाओं की संभावनाओं को जोड़ना होगा।
5. चरण 3 और 4 को तब तक दोहराएँ जब तक आप अंतिम नोड, यानी प्रयोग के संभावित अंत तक नहीं पहुँच जाते।

ध्यान दें कि एक स्तर में शाखाओं की संख्या जरूरी नहीं कि दूसरे स्तर में शाखाओं की संख्या के बराबर हो। इसी प्रकार, संभावित परिणाम से उत्पन्न होने वाली शाखाओं की संख्या समान स्तर के भीतर भी भिन्न हो सकती है।

वृक्ष उदाहरण

अब जब हम वृक्ष आरेख बनाने की परिभाषा और सिद्धांत को जानते हैं, तो आइए अवधारणा को बेहतर ढंग से समझने के लिए चरण दर चरण वास्तविक दुनिया के उदाहरण को देखें।

• तीन स्वतंत्र सिक्कों के सिक्के उछालने की संभाव्यता वृक्ष की रचना कीजिए। फिर तीनों उछालों पर चित आने की प्रायिकता ज्ञात कीजिए।

लॉटरी निकालते समय, केवल दो संभावित परिणाम होते हैं, हम चित या पट प्राप्त कर सकते हैं। इसलिए, सिक्का उछालने पर चित या पट आने की प्रायिकता है:

एक बार जब हम संभावित परिणामों की संभावनाओं को जान लेते हैं, तो हम वृक्ष आरेख का प्रतिनिधित्व करने के लिए आगे बढ़ते हैं।

चूंकि सिक्का उछालना स्वतंत्र होता है, इसलिए प्रत्येक उछाल में चित या पट आने की संभावना हमेशा समान रहेगी। इसलिए, पेड़ बनाने के लिए, दो शाखाओं (सिर और पूंछ) को प्रत्येक फेंके जाने के लिए समान संभावना के साथ दर्शाया जाना चाहिए।

और एक बार जब हम पेड़ बना लेते हैं, तो हमें बस तीन सिक्के उछालने की संभावना निर्धारित करनी होती है।

इसलिए, इस मामले में हमें शीर्ष पाने की सभी संभावनाओं को गुणा करना चाहिए, क्योंकि ये उस पथ की संभावनाएं हैं जो हमें वांछित परिणाम तक ले जाती हैं।

इस प्रकार, तीन सिक्के उछालने पर चित आने की प्रायिकता की गणना इस प्रकार की जाती है:

संक्षेप में, लगातार तीन बार चित आने की संभावना 12.5% है।

हल वृक्ष व्यायाम

एक गाँव में केवल 3 क्रेच हैं: 60% बच्चे क्रेच A में जाते हैं, 30% क्रेच B में और 10% क्रेच C में जाते हैं। इसके अलावा, तीन क्रेच में, 55% लोग लड़कियाँ हैं। पेड़ बनाएं और निम्नलिखित संभावनाओं की गणना करें:

• संभावना है कि जब एक बच्चे को यादृच्छिक रूप से चुना जाता है, तो वह डेकेयर बी की एक लड़की है।
• संभावना है कि जब किसी डेकेयर सेंटर से यादृच्छिक रूप से एक बच्चे का चयन किया जाता है, तो वह एक लड़का होगा।

ध्यान दें कि यदि सभी डेकेयर में लड़कियों का अनुपात 55% है, तो लड़कों के प्रतिशत की गणना केवल 1 माइनस 0.55 घटाकर की जाती है:

अब जब हम सभी संभावनाओं को जानते हैं, तो हम सभी संभावनाओं के साथ संभाव्यता वृक्ष बना सकते हैं:

इस प्रकार, डेकेयर बी से एक लड़की को यादृच्छिक रूप से चुनने की संभावना की गणना निम्नानुसार की जाती है:

दूसरी ओर, किसी भी डेकेयर में एक लड़के को चुनने की संभावना निर्धारित करने के लिए, हमें पहले प्रत्येक डेकेयर के लिए एक लड़के को चुनने की संभावना ढूंढनी होगी, फिर उन्हें एक साथ जोड़ना होगा:

वृक्ष संरचना के लाभ

वृक्ष संरचना की विशेषताओं के कारण, इस प्रकार के सांख्यिकीय ग्राफ़ के लाभ इस प्रकार हैं:

• निर्णय लेने के लिए वृक्ष आरेख बहुत उपयोगी होते हैं।
• सभी संभावित परिणामों के बीच संबंध को रेखांकन द्वारा दर्शाया जा सकता है।
• किसी समस्या का मूल कारण ढूंढना बहुत सुविधाजनक है।
• संभाव्यता और सांख्यिकी समस्याओं को हल करना आसान बनाता है।
• एक वृक्ष आरेख विचारों को व्यवस्थित करने और स्थिति का विश्लेषण करने में मदद करता है।