आर में फिट की कमी का परीक्षण कैसे करें (चरण दर चरण)

फिट परीक्षण की कमी का उपयोग यह निर्धारित करने के लिए किया जाता है कि पूर्ण प्रतिगमन मॉडल मॉडल के कम संस्करण की तुलना में डेटा सेट के लिए काफी बेहतर फिट प्रदान करता है या नहीं।

उदाहरण के लिए, मान लें कि हम एक निश्चित कॉलेज में छात्रों के लिए परीक्षा स्कोर की भविष्यवाणी करने के लिए अध्ययन किए गए घंटों की संख्या का उपयोग करना चाहते हैं। हम निम्नलिखित दो प्रतिगमन मॉडल को अनुकूलित करने का निर्णय ले सकते हैं:

पूर्ण मॉडल: स्कोर = β ₀ + बी ₁ (घंटे) + बी ₂ (घंटे) ²

कम किया गया मॉडल: स्कोर = β ₀ + बी ₁ (घंटे)

निम्नलिखित चरण-दर-चरण उदाहरण दिखाता है कि आर में फिट की कमी का परीक्षण कैसे किया जाए ताकि यह निर्धारित किया जा सके कि पूर्ण मॉडल कम किए गए मॉडल की तुलना में काफी बेहतर फिट प्रदान करता है या नहीं।

चरण 1: एक डेटासेट बनाएं और विज़ुअलाइज़ करें

सबसे पहले, हम एक डेटासेट बनाने के लिए निम्नलिखित कोड का उपयोग करेंगे जिसमें 50 छात्रों के लिए अध्ययन किए गए घंटों की संख्या और अर्जित परीक्षा स्कोर शामिल होंगे:

 #make this example reproducible
set. seeds (1)

#create dataset
df <- data. frame (hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(df)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

इसके बाद, हम घंटों और स्कोर के बीच संबंध को देखने के लिए एक स्कैटरप्लॉट बनाएंगे:

 #load ggplot2 visualization package
library (ggplot2)

#create scatterplot
ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

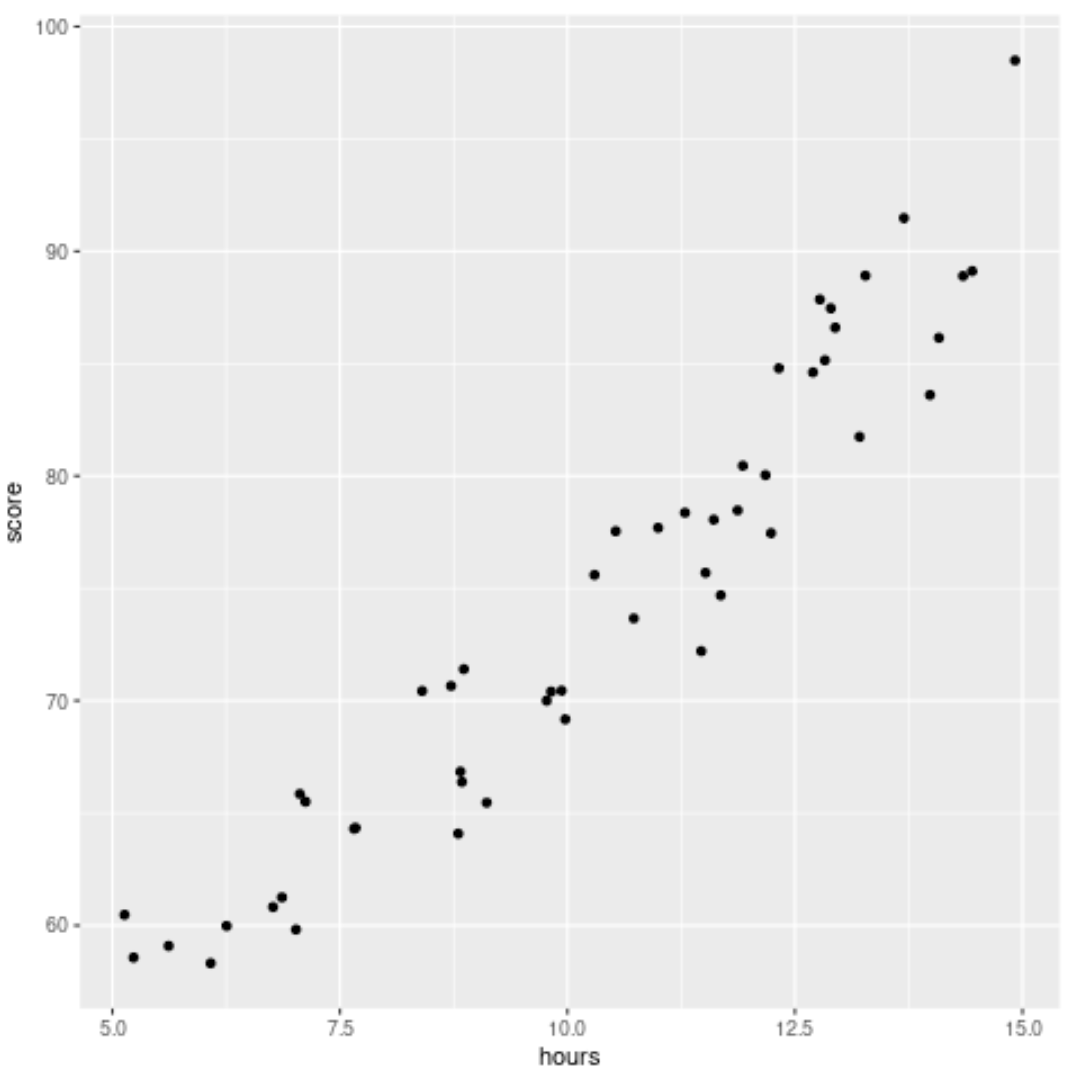
चरण 2: डेटासेट में दो अलग-अलग मॉडल फिट करें

इसके बाद, हम डेटासेट में दो अलग-अलग प्रतिगमन मॉडल फिट करेंगे:

 #fit full model
full <- lm(score ~ poly (hours,2), data=df)

#fit reduced model
reduced <- lm(score ~ hours, data=df)

चरण 3: फिट की कमी परीक्षण करें

इसके बाद, हम दो मॉडलों के बीच फिट की कमी का परीक्षण करने के लिए एनोवा() कमांड का उपयोग करेंगे:

 #lack of fit test
anova(full, reduced)

Analysis of Variance Table

Model 1: score ~ poly(hours, 2)
Model 2: score ~ hours
  Res.Df RSS Df Sum of Sq F Pr(>F)   
1 47 368.48                                
2 48 451.22 -1 -82.744 10.554 0.002144 **
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

एफ परीक्षण आँकड़ा 10.554 निकला और संबंधित पी-मान 0.002144 है। चूँकि यह पी-मान 0.05 से कम है, हम परीक्षण की शून्य परिकल्पना को अस्वीकार कर सकते हैं और निष्कर्ष निकाल सकते हैं कि पूर्ण मॉडल कम किए गए मॉडल की तुलना में सांख्यिकीय रूप से काफी बेहतर फिट प्रदान करता है।

चरण 4: अंतिम मॉडल की कल्पना करें

अंत में, हम मूल डेटासेट के विरुद्ध अंतिम मॉडल (पूर्ण मॉडल) की कल्पना कर सकते हैं:

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

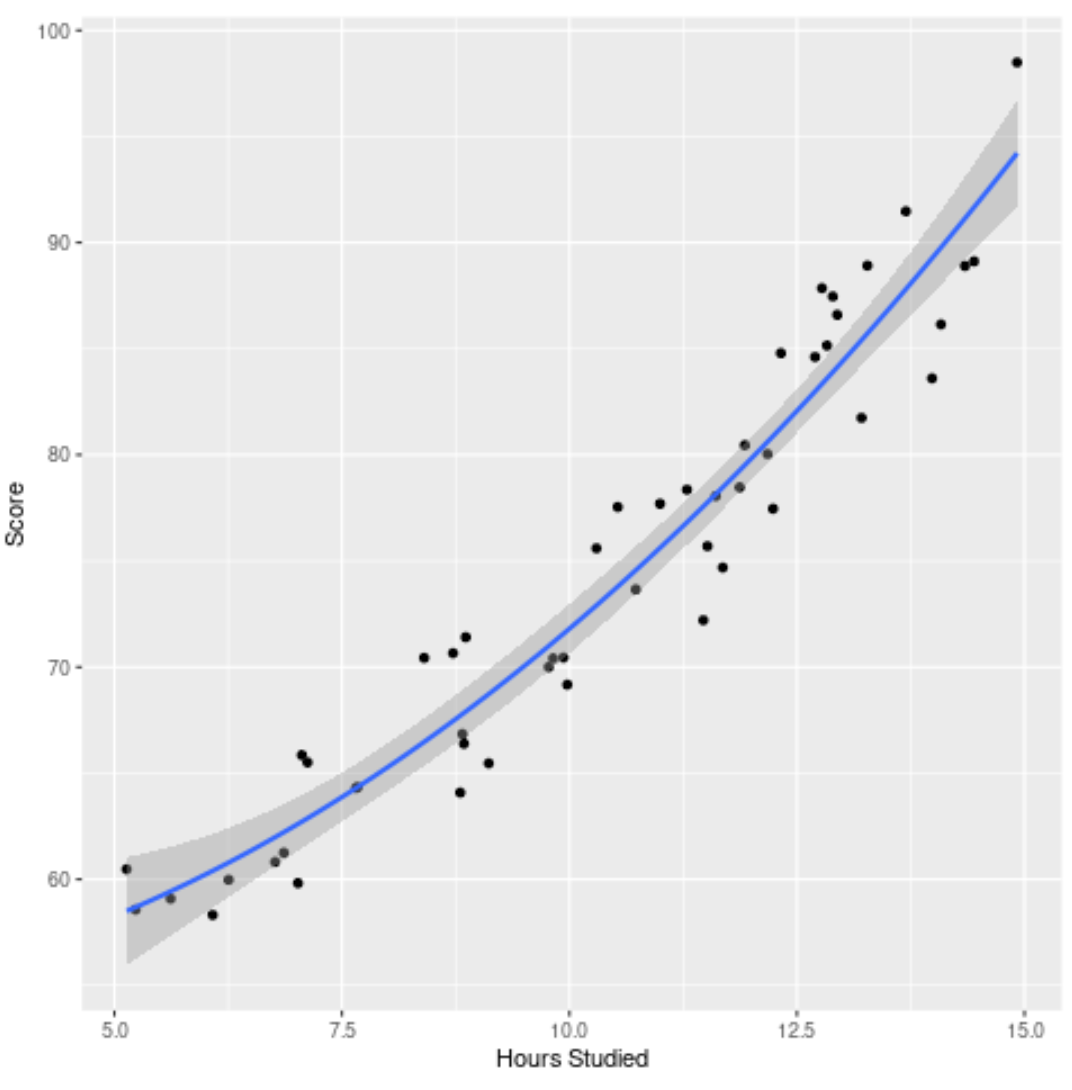
हम देख सकते हैं कि मॉडल वक्र डेटा को काफी अच्छी तरह से फिट बैठता है।

अतिरिक्त संसाधन

आर में सरल रैखिक प्रतिगमन कैसे करें
आर में मल्टीपल लीनियर रिग्रेशन कैसे करें
आर में बहुपद प्रतिगमन कैसे करें