वर्दी वितरण का एक परिचय

समान वितरण एक संभाव्यता वितरण है जिसमें a से b तक के अंतराल के बीच प्रत्येक मान के घटित होने की समान संभावना होती है।

यदि एक _{यादृच्छिक} चर _ _{_}

पी(एक्स ₁ < एक्स < एक्स ₂ ) = (एक्स ₂ – एक्स ₁ ) / (बी – ए)

सोना:

• x ₁ : कम ब्याज मूल्य
• x ₂ : ब्याज का ऊपरी मूल्य
• ए: न्यूनतम संभव मूल्य
• बी: अधिकतम संभव मूल्य

उदाहरण के लिए, मान लीजिए कि डॉल्फ़िन का वजन 100 और 150 पाउंड के बीच समान रूप से वितरित है।

यदि हम यादृच्छिक रूप से एक डॉल्फ़िन का चयन करते हैं, तो हम ऊपर दिए गए सूत्र का उपयोग करके यह संभावना निर्धारित कर सकते हैं कि चुनी गई डॉल्फ़िन का वजन 120 और 130 पाउंड के बीच है:

• पी(120 < एक्स < 130) = (130 – 120) / (150 – 100)
• पी(120 < एक्स < 130) = 10/50
• पी(120 < एक्स < 130) = 0.2

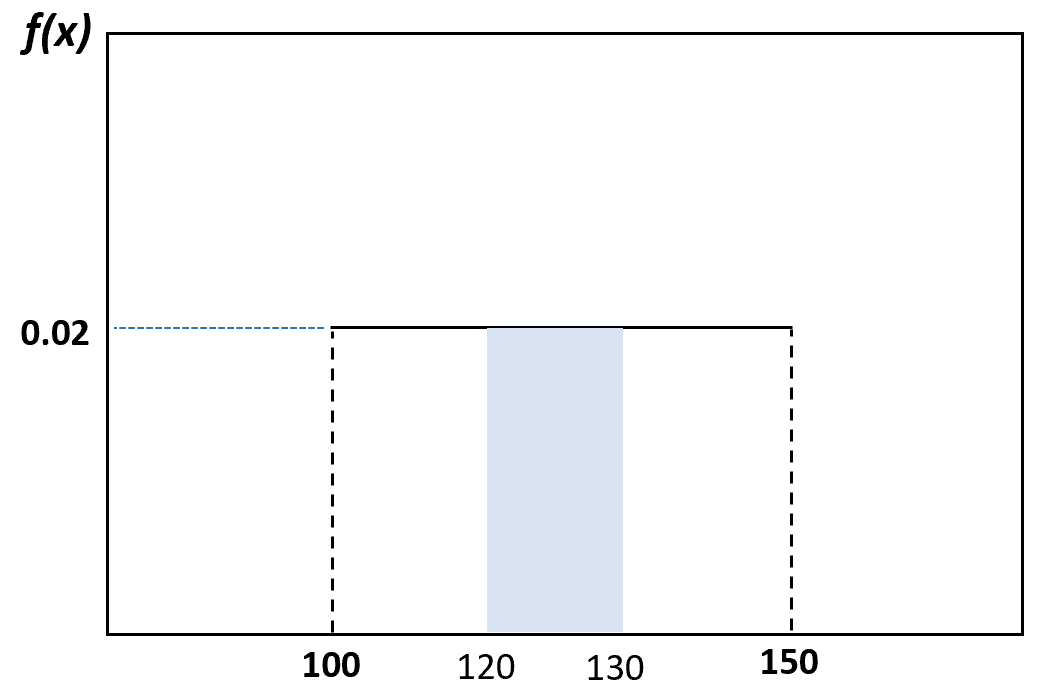
चुनी गई डॉल्फ़िन का वज़न 120 से 130 पाउंड के बीच होने की संभावना 0.2 है।

समान वितरण की कल्पना करें

यदि हम समान वितरण की कल्पना करने के लिए एक घनत्व प्लॉट बनाते हैं, तो यह निम्नलिखित प्लॉट जैसा दिखेगा:

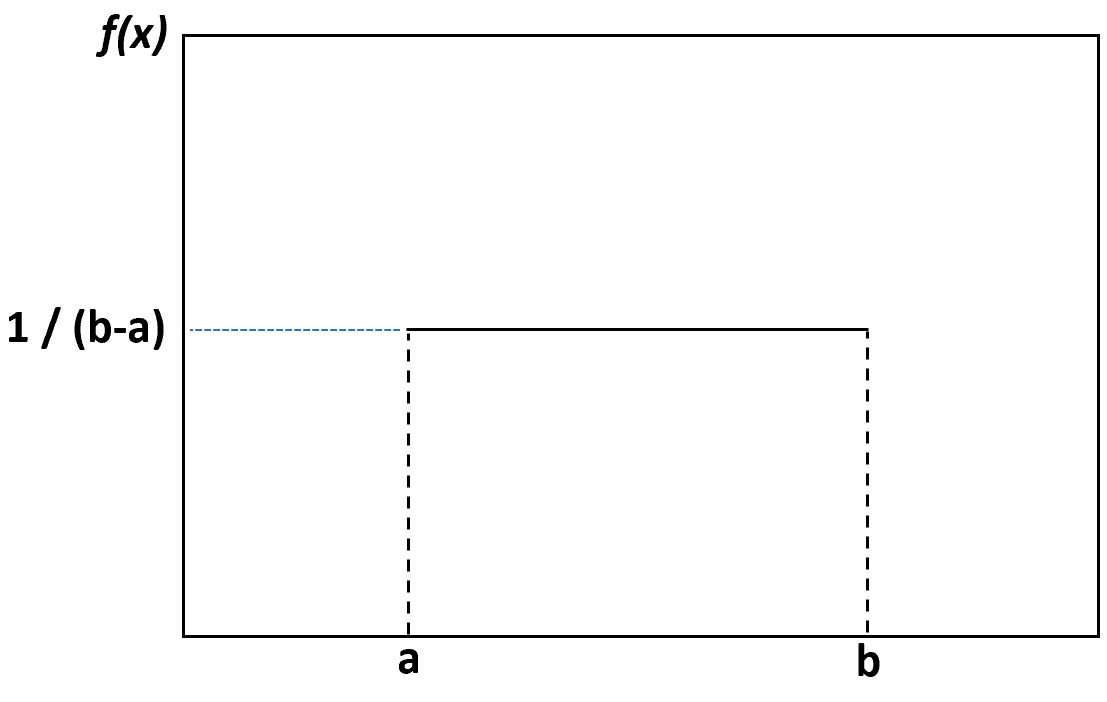
निचली सीमा a और ऊपरी सीमा b के बीच प्रत्येक मान के घटित होने की संभावना समान होती है और इन सीमाओं के बाहर किसी भी मान के घटित होने की संभावना शून्य होती है।

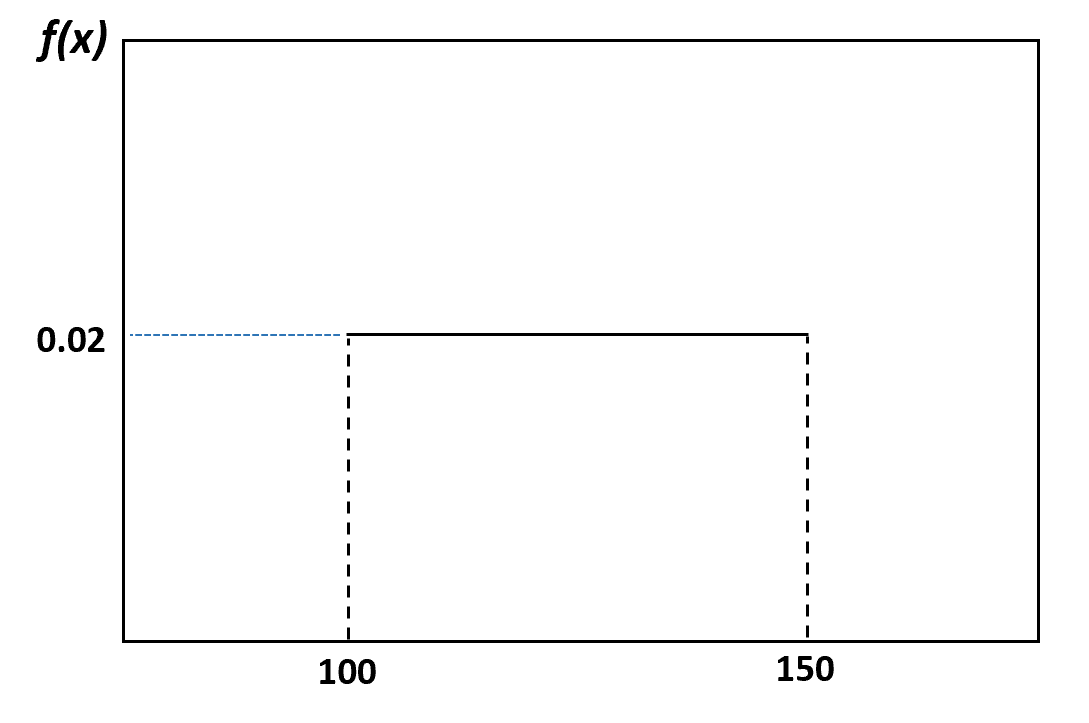
उदाहरण के लिए, हमारे पिछले उदाहरण में, हमने कहा था कि डॉल्फ़िन का वजन 100 और 150 पाउंड के बीच समान रूप से वितरित होता है। इस वितरण की कल्पना इस प्रकार करें:

और संभावना यह है कि बेतरतीब ढंग से चुनी गई डॉल्फ़िन का वजन 120 और 130 पाउंड के बीच है, इसकी कल्पना इस प्रकार की जा सकती है:

समान वितरण के गुण

समान वितरण में निम्नलिखित गुण होते हैं:

• औसत: (ए + बी) / 2
• माध्यिका: (ए + बी) / 2
• मानक विचलन: √ (बी – ए) ^2/12
• अंतर: (बी – ए) ^2/12

उदाहरण के लिए, मान लीजिए कि डॉल्फ़िन का वजन 100 और 150 पाउंड के बीच समान रूप से वितरित है।

हम इस वितरण के लिए निम्नलिखित गुणों की गणना कर सकते हैं:

• औसत वजन: (ए + बी) / 2 = (150 + 100) / 2 = 125
• माध्य भार: (ए + बी) / 2 = (150 + 100) / 2 = 125
• वजन का मानक विचलन: √ (150 – 100) ^2/12 = 14.43
• वज़न भिन्नता: (150 – 100) ^2/12 = 208.33

समान वितरण प्रथाओं से संबंधित मुद्दे

समान वितरण के बारे में अपने ज्ञान का परीक्षण करने के लिए निम्नलिखित अभ्यास समस्याओं का उपयोग करें।

प्रश्न 1: प्रत्येक 20 मिनट में एक बस बस स्टॉप पर आती है। यदि आप बस स्टॉप पर पहुंचते हैं, तो क्या संभावना है कि बस 8 मिनट या उससे कम समय में पहुंच जाएगी?

समाधान 1: न्यूनतम प्रतीक्षा समय 0 मिनट है और अधिकतम प्रतीक्षा समय 20 मिनट है। निम्न ब्याज मूल्य 0 मिनट है और ऊपरी ब्याज मूल्य 8 मिनट है।

इसलिए, हम संभाव्यता की गणना इस प्रकार करेंगे:

पी(0 < एक्स < 8) = (8-0) / (20-0) = 8/20 = 0.4 ।

प्रश्न 2: एनबीए गेम की अवधि 120 और 170 मिनट के बीच समान रूप से वितरित की जाती है। इसकी क्या प्रायिकता है कि यादृच्छिक रूप से चयनित NBA खेल 155 मिनट से अधिक चले?

समाधान 2: न्यूनतम अवधि 120 मिनट है और अधिकतम अवधि 170 मिनट है। निम्न ब्याज मूल्य 155 मिनट है और ऊपरी ब्याज मूल्य 170 मिनट है।

इसलिए, हम संभाव्यता की गणना इस प्रकार करेंगे:

पी(155 <एक्स <170) = (170-155) / (170-120) = 15/50 = 0.3 ।

प्रश्न 3: मेंढक की एक निश्चित प्रजाति का वजन 15 से 25 ग्राम के बीच समान रूप से वितरित होता है। यदि आप यादृच्छिक रूप से एक मेंढक का चयन करते हैं, तो इसकी क्या संभावना है कि इसका वजन 17 से 19 ग्राम के बीच हो?

समाधान 3: न्यूनतम वजन 15 ग्राम और अधिकतम वजन 25 ग्राम है। निम्न ब्याज मूल्य 17 ग्राम है और ऊपरी ब्याज मूल्य 19 ग्राम है।

इसलिए, हम संभाव्यता की गणना इस प्रकार करेंगे:

पी(17 < एक्स <19) = (19-17) / (25-15) = 2/10 = 0.2 ।

नोट: हम इनमें से प्रत्येक समस्या के उत्तर की जांच करने के लिए समान वितरण कैलकुलेटर का उपयोग कर सकते हैं।