बहुपद परीक्षण क्या है? (परिभाषा & #038; उदाहरण)
एक बहुपद परीक्षण का उपयोग यह निर्धारित करने के लिए किया जाता है कि क्या एक श्रेणीगत चर एक काल्पनिक वितरण का अनुसरण करता है।
यह परीक्षण निम्नलिखित शून्य और वैकल्पिक परिकल्पनाओं का उपयोग करता है:
एच 0 : एक श्रेणीबद्ध चर एक काल्पनिक वितरण का अनुसरण करता है।
एच ए : एक श्रेणीबद्ध चर काल्पनिक वितरण का पालन नहीं करता है ।
यदि परीक्षण का पी-मान महत्व के एक निश्चित स्तर से नीचे है (जैसे α = 0.05), तो हम शून्य परिकल्पना को अस्वीकार कर सकते हैं और निष्कर्ष निकाल सकते हैं कि चर परिकल्पित वितरण का पालन नहीं करता है।
इस परीक्षण का उपयोग तब किया जाता है जब कोई चर k भिन्न परिणाम ले सकता है। बहुपद परीक्षण का एक उत्कृष्ट उदाहरण वह है जहां हम यह निर्धारित करना चाहते हैं कि कुछ पासे निष्पक्ष हैं या नहीं। जब आप एक पासा घुमाते हैं, तो उसके प्रत्येक संख्या (1 से 6) पर गिरने की प्रायिकता 1/6 होती है।
यह जांचने के लिए कि कोई पासा निष्पक्ष है या नहीं, हम इसे कई बार घुमा सकते हैं और देख सकते हैं कि जितनी बार यह विभिन्न संख्याओं पर गिरता है, वह हमारी अपेक्षा से काफी भिन्न है।
निम्नलिखित उदाहरण दिखाते हैं कि आर सांख्यिकीय प्रोग्रामिंग भाषा का उपयोग करके बहुपद परीक्षण कैसे किया जाए।
उदाहरण 1: निष्पक्ष पासा
मान लीजिए हम यह निर्धारित करना चाहते हैं कि पासा उचित है या नहीं। इसका परीक्षण करने के लिए, हम इसे 30 बार चलाते हैं और प्रत्येक परिणाम की आवृत्ति रिकॉर्ड करते हैं। निम्न तालिका परिणाम दिखाती है:
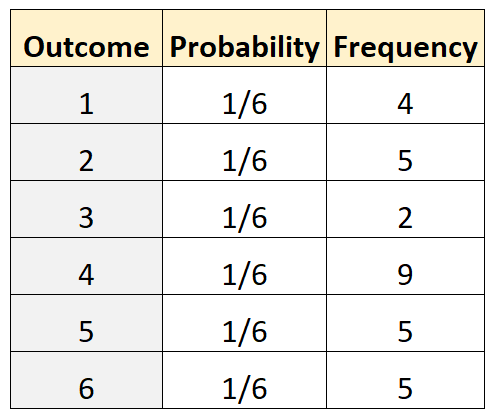
R में निम्नलिखित कोड का उपयोग बहुपद परीक्षण करने के लिए किया जा सकता है:
library (EMT)
#specify probability of each outcome
prob <- c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)
#specify frequency of each outcome from experiment
actual <- c(4, 5, 2, 9, 5, 5)
#perform multinomial test
multinomial. test (actual, prob)
Exact Multinomial Test, distance measure: p
Events pObs p.value
324632 0 0.4306
परीक्षण का पी-मान 0.4306 है। चूँकि यह पी-मान 0.05 से कम नहीं है, हम शून्य परिकल्पना को अस्वीकार नहीं करेंगे। इसलिए हमारे पास यह कहने के लिए पर्याप्त सबूत नहीं हैं कि पासे अनुचित हैं।
उदाहरण 2: उत्पाद की बिक्री
मान लीजिए कि एक स्टोर मालिक यह अनुमान लगाता है कि समान संख्या में ग्राहक चार अलग-अलग उत्पादों में से प्रत्येक को खरीदेंगे। इसका परीक्षण करने के लिए, यह उन ग्राहकों की संख्या रिकॉर्ड करता है जिन्होंने किसी दिए गए सप्ताह में प्रत्येक उत्पाद खरीदा है। निम्न तालिका परिणाम दिखाती है:
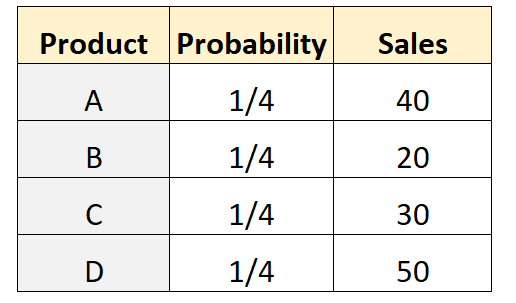
इस डेटासेट पर बहुपद परीक्षण करने के लिए R में निम्नलिखित कोड का उपयोग किया जा सकता है:
library (EMT)
#specify probability of each outcome
prob <- c(1/4, 1/4, 1/4, 1/4)
#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)
#perform multinomial test
multinomial. test (actual, prob)
Exact Multinomial Test, distance measure: p
Events pObs p.value
477191 0 0.00226
परीक्षण का पी-मान 0.00226 है। चूँकि यह पी-मान 0.05 से कम है, हम शून्य परिकल्पना को अस्वीकार कर देंगे। इसलिए, हमारे पास यह कहने के लिए पर्याप्त सबूत हैं कि प्रत्येक उत्पाद की बिक्री समान नहीं है।
उदाहरण 3: एक थैले में पत्थर
टॉम का कहना है कि एक बैग से लाल, हरा या बैंगनी संगमरमर चुनने की संभावना क्रमशः 0.2, 0.5 और 0.3 है। इसका परीक्षण करने के लिए, उसका दोस्त माइक बैग में हाथ डालता है और 100 अलग-अलग बार एक मार्बल (प्रतिस्थापन के साथ) बाहर निकालता है। निम्न तालिका परिणाम दिखाती है:
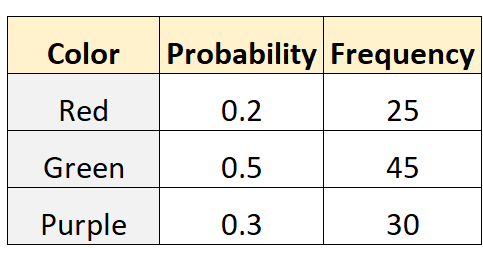
इस डेटासेट पर बहुपद परीक्षण करने के लिए R में निम्नलिखित कोड का उपयोग किया जा सकता है:
library (EMT)
#specify probability of each outcome
prob <- c(.2, .5, .3)
#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)
#perform multinomial test
multinomial. test (actual, prob)
Exact Multinomial Test, distance measure: p
Events pObs p.value
5151 0.0037 0.3999
परीक्षण का पी-वैल्यू 0.3999 है। चूँकि यह पी-मान 0.05 से कम नहीं है, हम शून्य परिकल्पना को अस्वीकार करने में विफल रहेंगे। इसलिए हमारे पास यह कहने के लिए पर्याप्त सबूत नहीं हैं कि बैग में मार्बल्स का वितरण टॉम द्वारा निर्दिष्ट से अलग है।
अतिरिक्त संसाधन
लेखक के बारे में
डॉ. बेंजामिन एंडरसन
नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने