अनुमान की मानक त्रुटि क्या है? (परिभाषा & #038; उदाहरण)

अनुमान की मानक त्रुटि एक प्रतिगमन मॉडल द्वारा की गई भविष्यवाणियों की सटीकता को मापने का एक तरीका है।

अक्सर नोट किया जाता है σ _est , इसकी गणना इस प्रकार की जाती है:

σ = √ Σ(y – ŷ) ² /n _है

सोना:

• y: प्रेक्षित मान
• ŷ: अनुमानित मूल्य
• n: अवलोकनों की कुल संख्या

अनुमान की मानक त्रुटि हमें यह अंदाज़ा देती है कि एक प्रतिगमन मॉडल किसी डेटा सेट में कितनी अच्छी तरह फिट बैठता है। विशेष रूप से:

• मूल्य जितना छोटा होगा, फिट उतना ही बेहतर होगा।
• मूल्य जितना बड़ा होगा, फिट उतना ही खराब होगा।

अनुमान की एक छोटी मानक त्रुटि वाले प्रतिगमन मॉडल के लिए, डेटा बिंदुओं को अनुमानित प्रतिगमन रेखा के आसपास कसकर क्लस्टर किया जाएगा:

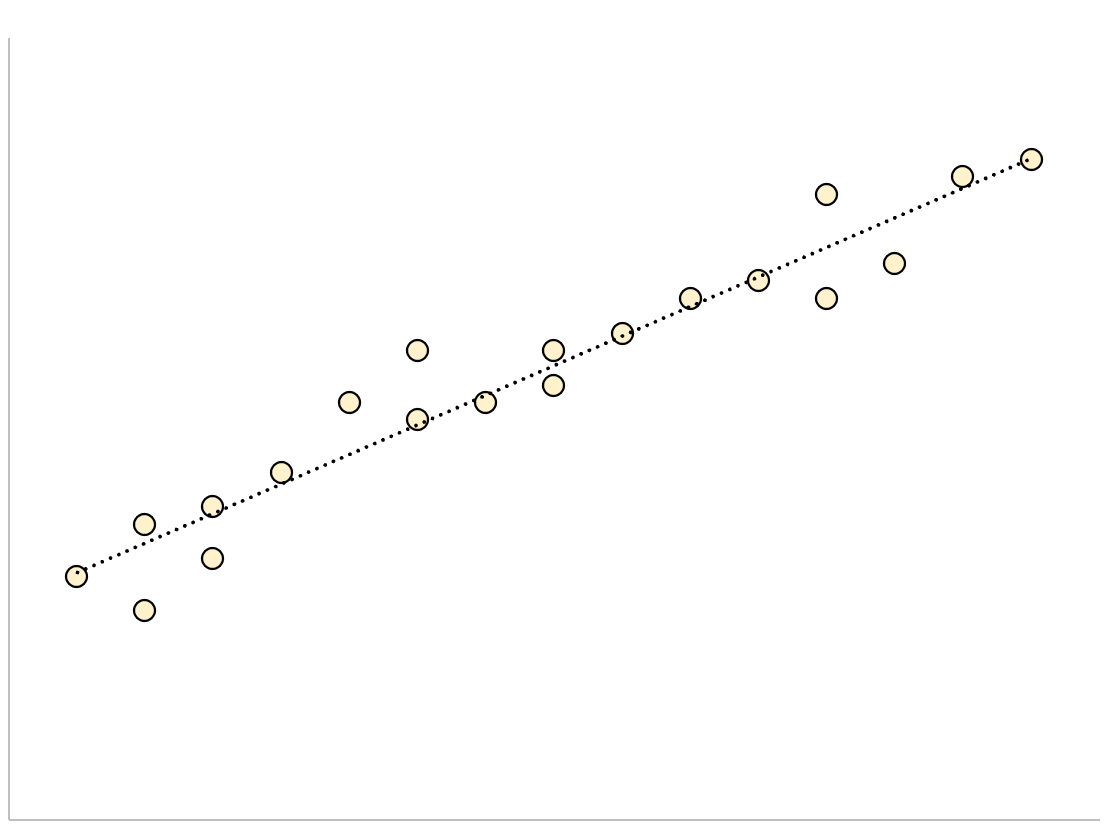
इसके विपरीत, अनुमान की बड़ी मानक त्रुटि वाले प्रतिगमन मॉडल के लिए, डेटा बिंदु प्रतिगमन रेखा के चारों ओर अधिक ढीले ढंग से बिखरे होंगे:

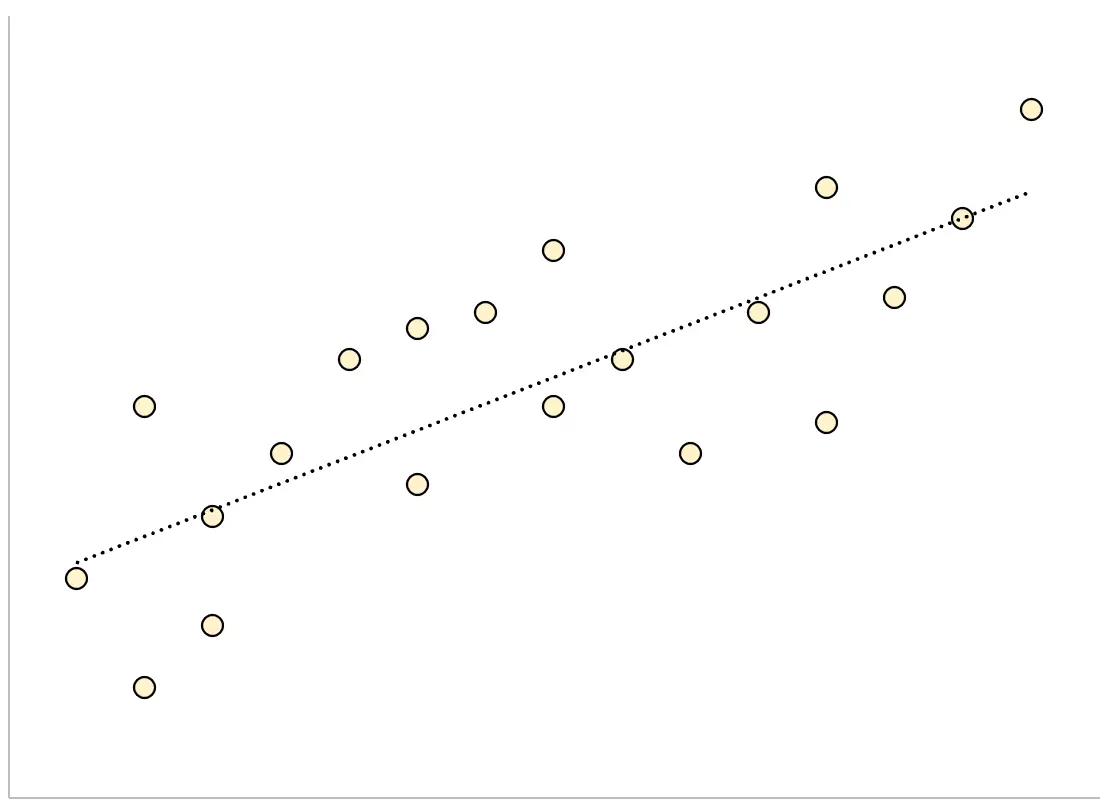
निम्नलिखित उदाहरण दिखाता है कि एक्सेल में प्रतिगमन मॉडल के लिए अनुमान की मानक त्रुटि की गणना और व्याख्या कैसे करें।

उदाहरण: एक्सेल में अनुमान की मानक त्रुटि

Excel में प्रतिगमन मॉडल के अनुमान की मानक त्रुटि की गणना करने के लिए निम्नलिखित चरणों का उपयोग करें।

चरण 1: डेटा दर्ज करें

सबसे पहले, डेटासेट मान दर्ज करें:

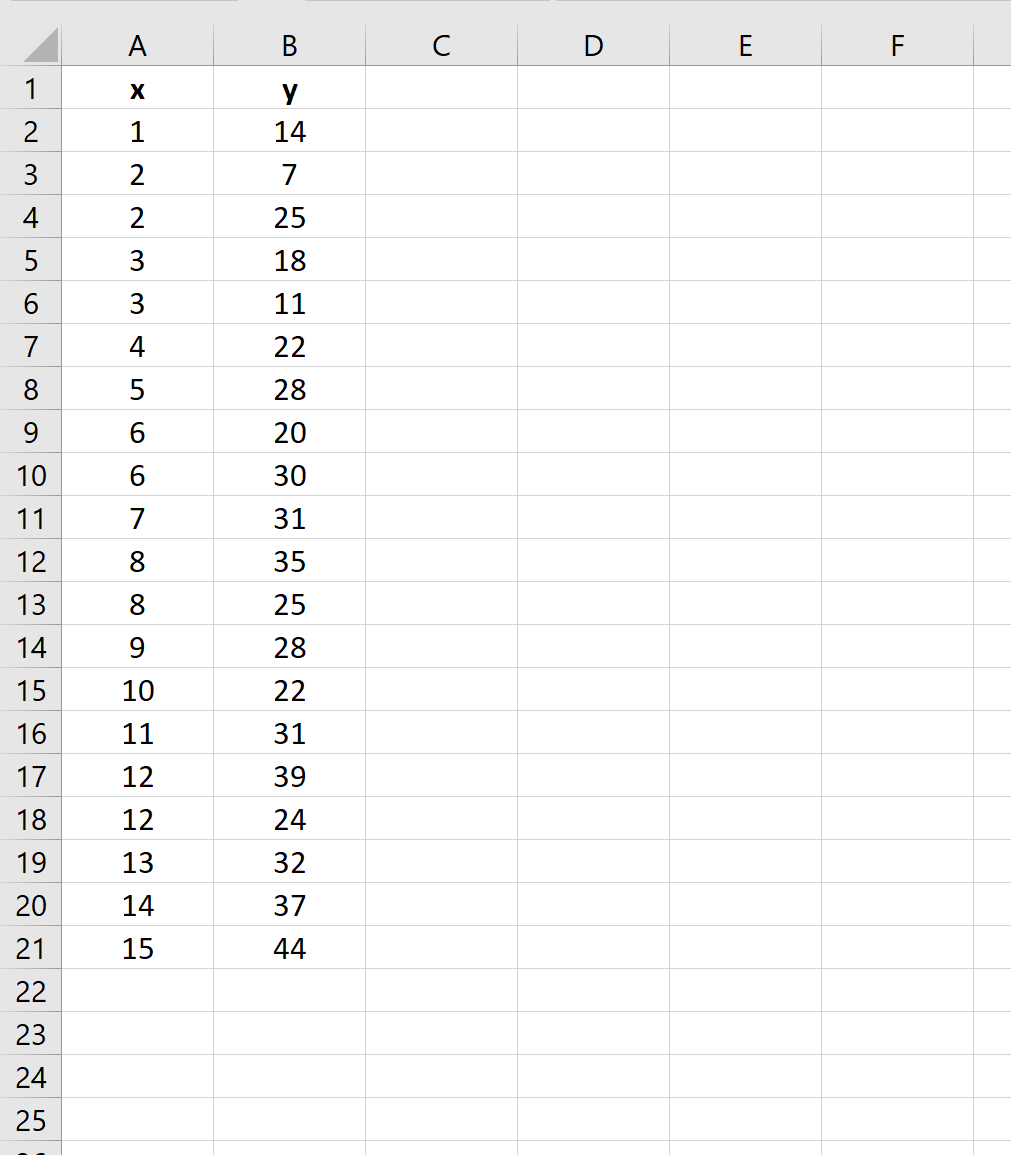
चरण 2: रेखीय प्रतिगमन करें

इसके बाद, शीर्ष रिबन के साथ डेटा टैब पर क्लिक करें। इसके बाद एनालाइज ग्रुप में डेटा एनालिसिस विकल्प पर क्लिक करें।

यदि आपको यह विकल्प दिखाई नहीं देता है, तो आपको पहले विश्लेषण टूलपैक लोड करना होगा।

दिखाई देने वाली नई विंडो में, रिग्रेशन पर क्लिक करें और फिर ओके पर क्लिक करें।

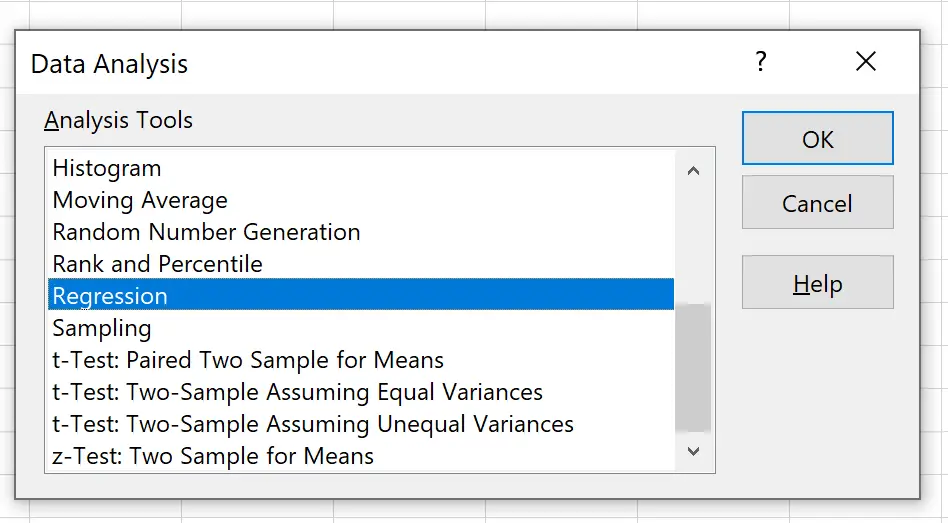
दिखाई देने वाली नई विंडो में, निम्नलिखित जानकारी प्रदान करें:

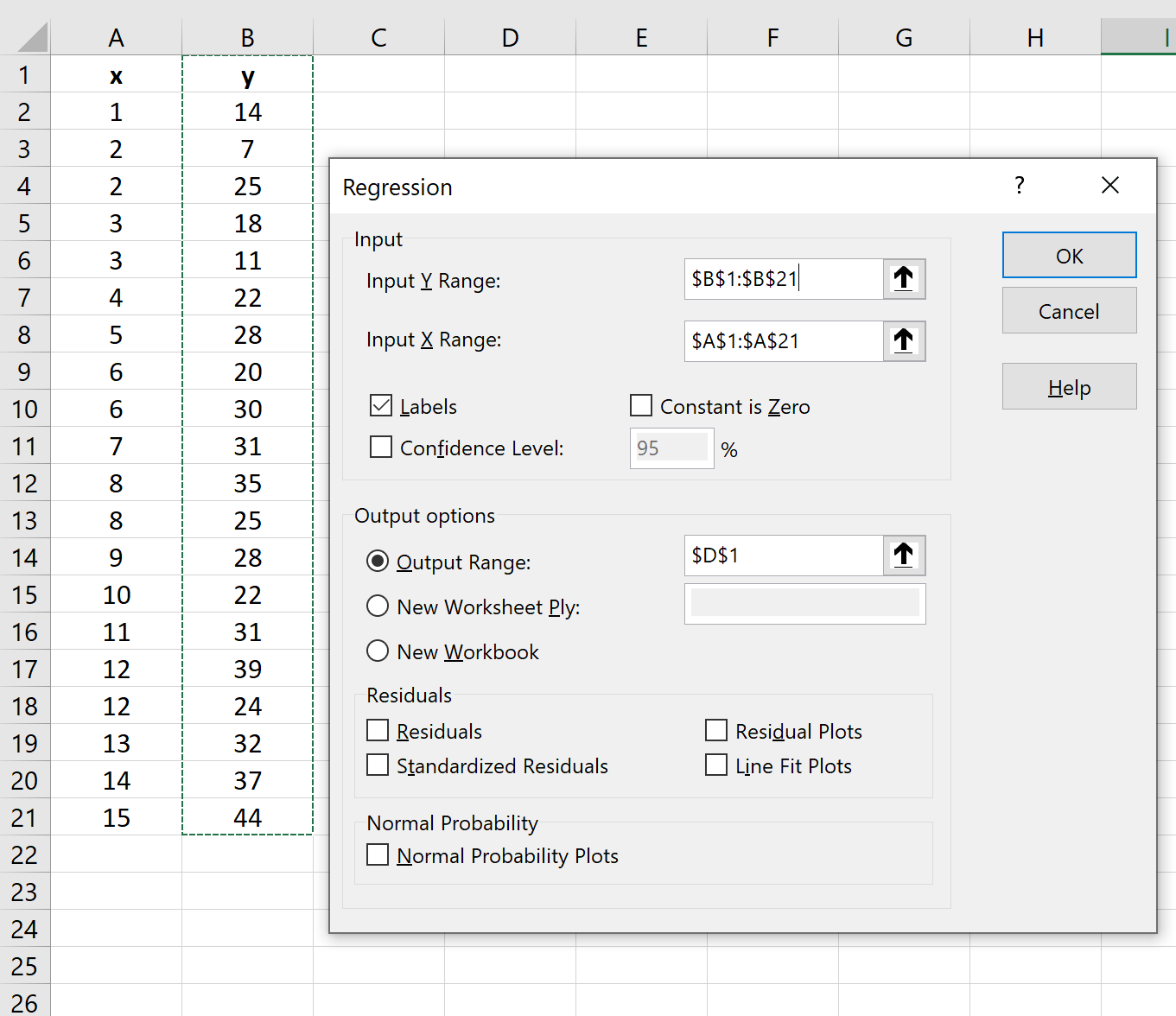
एक बार जब आप ओके पर क्लिक करेंगे, तो रिग्रेशन परिणाम दिखाई देगा:

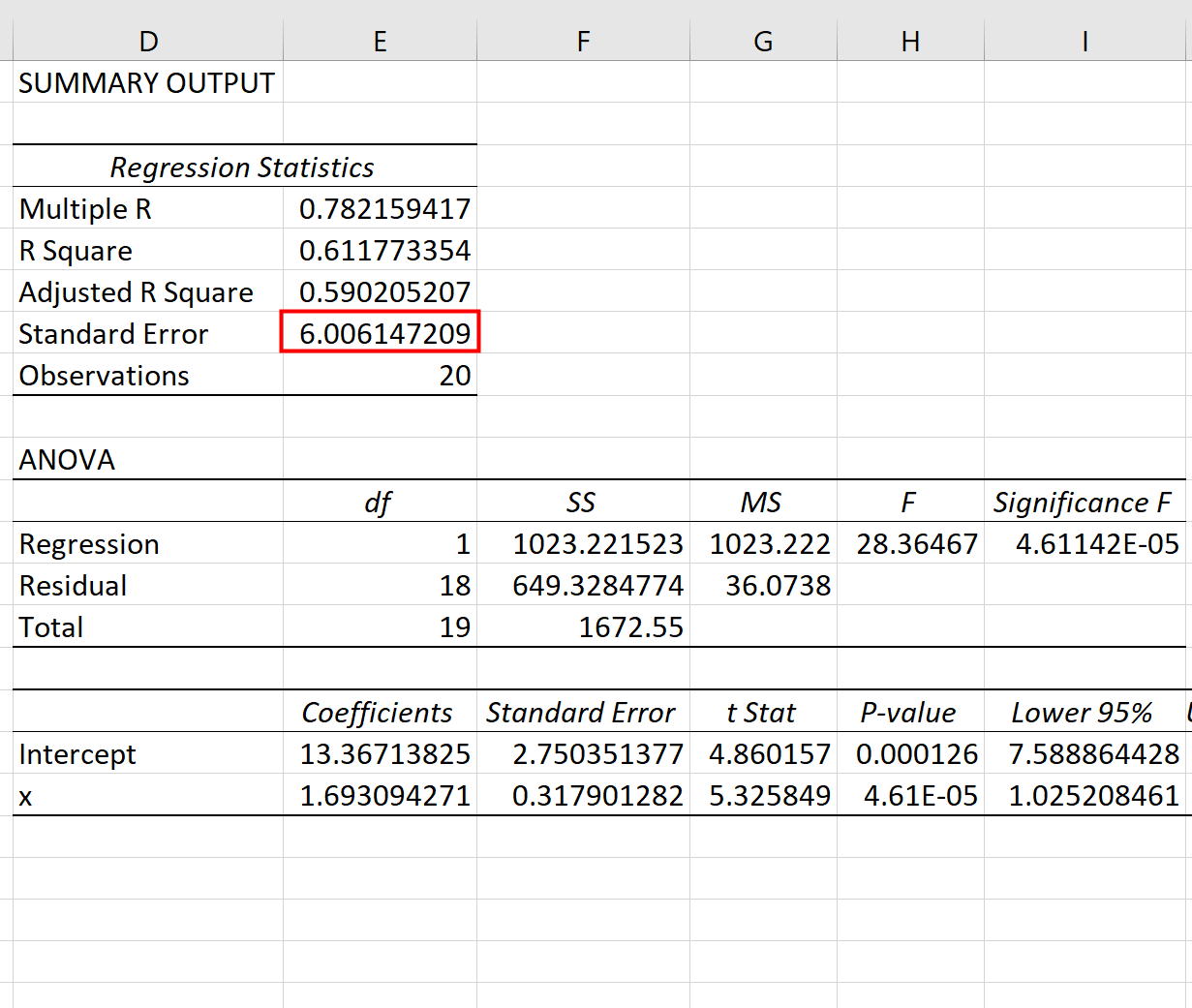
अनुमानित प्रतिगमन समीकरण बनाने के लिए हम प्रतिगमन तालिका से गुणांक का उपयोग कर सकते हैं:

ŷ = 13.367 + 1.693(x)

और हम देख सकते हैं कि इस प्रतिगमन मॉडल के अनुमान की मानक त्रुटि 6.006 है। सरल शब्दों में, यह हमें बताता है कि औसत डेटा बिंदु प्रतिगमन रेखा से 6.006 इकाई दूर है।

हम एक निश्चित डेटा बिंदु के अनुमानित मूल्य के लिए 95% विश्वास अंतराल का निर्माण करने के लिए अनुमानित प्रतिगमन समीकरण और अनुमान की मानक त्रुटि का उपयोग कर सकते हैं।

उदाहरण के लिए, मान लीजिए x 10 के बराबर है। अनुमानित प्रतिगमन समीकरण का उपयोग करके, हम अनुमान लगाएंगे कि y बराबर होगा:

ŷ = 13.367 + 1.693*(10) = 30.297

और हम निम्नलिखित सूत्र का उपयोग करके इस अनुमान के लिए 95% विश्वास अंतराल प्राप्त कर सकते हैं:

• 95% सीआई = [ŷ – 1.96*σ _है , ŷ + 1.96*σ _है ]

हमारे उदाहरण के लिए, 95% विश्वास अंतराल की गणना इस प्रकार की जाएगी:

• 95% सीआई = [ŷ – 1.96*σ _है , ŷ + 1.96*σ _है ]
• 95% सीआई = [30.297 – 1.96*6.006, 30.297 + 1.96*6.006]
• 95% सीआई = [18,525, 42,069]

अतिरिक्त संसाधन

एक्सेल में सरल रैखिक प्रतिगमन कैसे करें
एक्सेल में मल्टीपल लीनियर रिग्रेशन कैसे करें
एक्सेल में एक अवशिष्ट प्लॉट कैसे बनाएं