एक्सेल में घातीय वितरण का उपयोग कैसे करें

घातीय वितरण एक संभाव्यता वितरण है जिसका उपयोग उस समय को मॉडल करने के लिए किया जाता है जब हमें किसी निश्चित घटना के घटित होने तक प्रतीक्षा करनी होती है।

इस वितरण का उपयोग प्रश्नों के उत्तर देने के लिए किया जा सकता है जैसे:

• एक खुदरा विक्रेता को अपने स्टोर में ग्राहक के प्रवेश के लिए कितनी देर तक प्रतीक्षा करनी चाहिए?
• ख़त्म होने से पहले बैटरी कितने समय तक काम करती रहेगी?
• खराब होने से पहले कंप्यूटर कितने समय तक काम करता रहेगा?

प्रत्येक परिदृश्य में, हम यह गणना करना चाहते हैं कि किसी निश्चित घटना के घटित होने तक हमें कितने समय तक प्रतीक्षा करनी होगी। इस प्रकार, प्रत्येक परिदृश्य को घातीय वितरण का उपयोग करके मॉडल किया जा सकता है।

यदि एक यादृच्छिक चर X एक घातीय वितरण का अनुसरण करता है, तो X का संचयी घनत्व फ़ंक्शन लिखा जा सकता है:

एफ (एक्स; λ) = 1 – ई ^-λx

सोना:

• λ: दर पैरामीटर (λ = 1/μ के रूप में गणना)
• ई: एक स्थिरांक लगभग 2.718 के बराबर

एक्सेल में घातीय वितरण के संचयी घनत्व फ़ंक्शन से संबंधित संभावनाओं की गणना करने के लिए, हम निम्नलिखित सूत्र का उपयोग कर सकते हैं:

 =EXPON.DIST(x, lambda, cumulative)

सोना:

• x : घातीय रूप से वितरित यादृच्छिक चर का मान
• लैम्ब्डा : दर पैरामीटर
• संचयी : संचयी घनत्व फ़ंक्शन का उपयोग करना है या नहीं (सही या गलत)

निम्नलिखित उदाहरण दिखाते हैं कि व्यवहार में इस सूत्र का उपयोग कैसे करें।

उदाहरण 1: अगले ग्राहक के आने तक का समय

औसतन हर दो मिनट में एक नया ग्राहक स्टोर में प्रवेश करता है। किसी ग्राहक के आने के बाद, एक मिनट से भी कम समय में नए ग्राहक के आने की प्रायिकता निर्धारित करें।

समाधान: ग्राहकों के बीच औसत समय दो मिनट है। इस प्रकार, दर की गणना निम्नानुसार की जा सकती है:

• λ = 1/µ
• λ = 1/2
• λ = 0.5

इसलिए, हम एक मिनट से भी कम समय में नए ग्राहक के आने की संभावना की गणना करने के लिए एक्सेल में निम्नलिखित सूत्र का उपयोग कर सकते हैं:

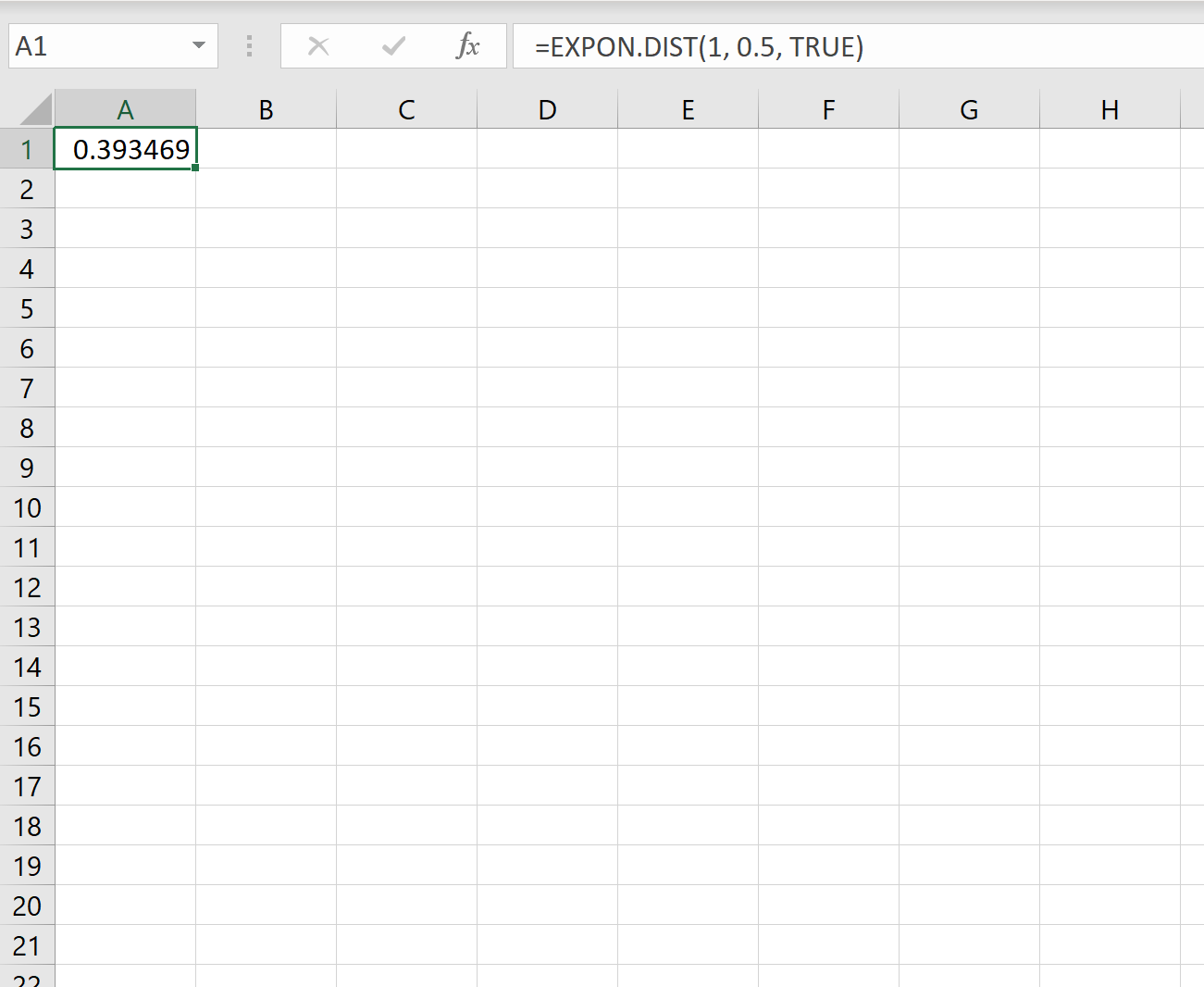
अगले ग्राहक के आने के लिए हमें एक मिनट से भी कम समय तक इंतजार करना होगा इसकी संभावना 0.393469 है।

उदाहरण 2: अगले भूकंप का समय

मान लीजिए कि एक निश्चित क्षेत्र में औसतन हर 400 दिन में एक भूकंप आता है। भूकंप के बाद, संभावना निर्धारित करें कि अगला भूकंप आने में 500 दिन से अधिक का समय लगेगा।

समाधान: भूकंपों के बीच का औसत समय 400 दिन है। इस प्रकार, दर की गणना निम्नानुसार की जा सकती है:

• λ = 1/µ
• λ = 1/400
• λ = 0.0025

इसलिए, हम इस संभावना की गणना करने के लिए एक्सेल में निम्नलिखित सूत्र का उपयोग कर सकते हैं कि अगला भूकंप आने में 500 दिन से कम समय लगेगा:

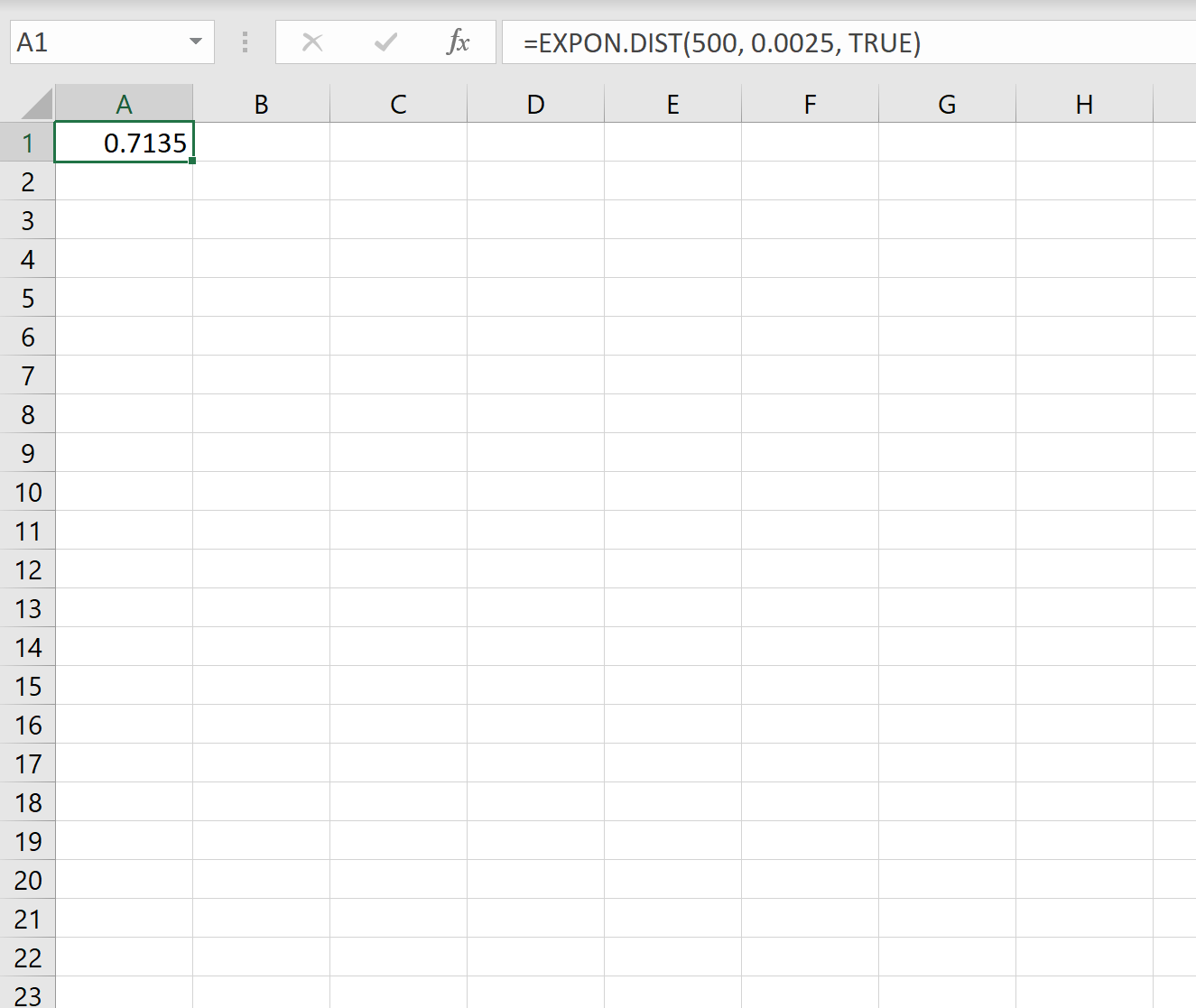
अगले भूकंप के 500 दिन से कम समय होने की संभावना 0.7135 है।

तो संभावना है कि हमें अगले भूकंप के लिए 500 दिनों से अधिक इंतजार करना होगा 1 – 0.7135 = 0.2865 ।

उदाहरण 3: अगले फ़ोन कॉल तक का समय

मान लीजिए कि एक कॉल सेंटर को औसतन हर 10 मिनट में एक नई कॉल प्राप्त होती है। किसी ग्राहक के कॉल करने के बाद, संभावना निर्धारित करें कि कोई नया ग्राहक 10 से 15 मिनट के भीतर कॉल करेगा।

समाधान: कॉल के बीच का औसत समय 10 मिनट है। इस प्रकार, दर की गणना निम्नानुसार की जा सकती है:

• λ = 1/µ
• λ = 1/10
• λ = 0.1

इसलिए, हम इस संभावना की गणना करने के लिए एक्सेल में निम्नलिखित सूत्र का उपयोग कर सकते हैं कि अगला ग्राहक 10 से 15 मिनट के भीतर कॉल करेगा:

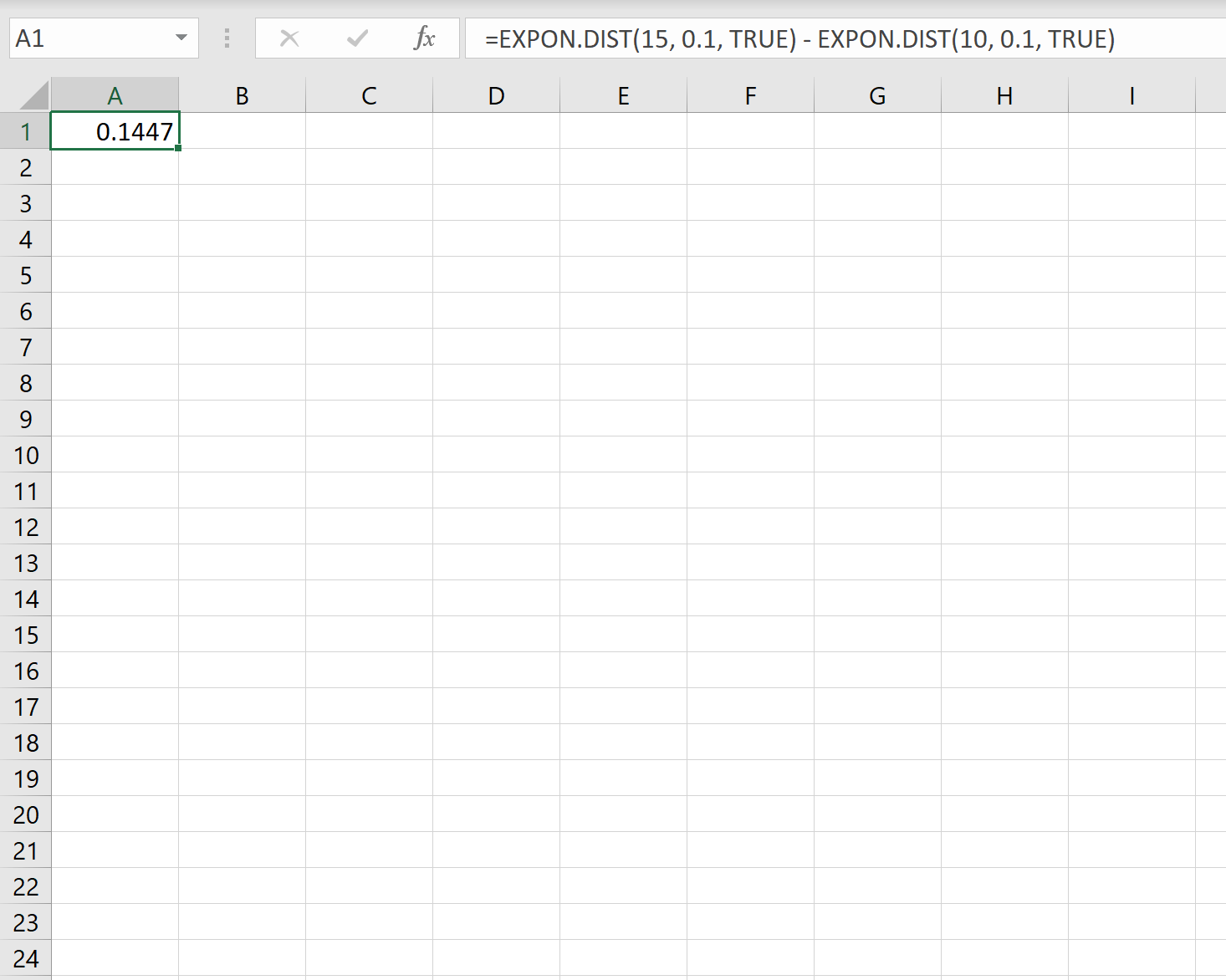
संभावना है कि कोई नया ग्राहक 10-15 मिनट के भीतर कॉल करेगा। 0.1447 है.

अतिरिक्त संसाधन

घातीय वितरण का एक परिचय
घातीय वितरण की स्मृतिहीन संपत्ति
आर में घातीय वितरण कैसे प्लॉट करें