निरंतर भिन्नता परिकल्पना: परिभाषा और उदाहरण

रैखिक प्रतिगमन एक ऐसी तकनीक है जिसका उपयोग हम एक या अधिक भविष्यवक्ता चर और एक प्रतिक्रिया चर के बीच संबंध को मापने के लिए करते हैं।

रैखिक प्रतिगमन की प्रमुख धारणाओं में से एक यह है कि भविष्यवक्ता चर के प्रत्येक स्तर पर अवशेषों में निरंतर भिन्नता होती है।

यदि इस धारणा को सत्यापित नहीं किया जाता है, तो अवशेष विषमलैंगिकता से पीड़ित होंगे। जब ऐसा होता है, तो मॉडल गुणांक अनुमान अविश्वसनीय हो जाते हैं।

निरंतर विचरण का मूल्यांकन कैसे करें

यह निर्धारित करने का सबसे आम तरीका है कि प्रतिगमन मॉडल के अवशेषों में निरंतर भिन्नता है या नहीं, अवशेषों के खिलाफ फिट मूल्यों का एक प्लॉट बनाना है।

यह एक प्रकार का प्लॉट है जो x-अक्ष के साथ प्रतिगमन मॉडल के फिट किए गए मानों और y-अक्ष के साथ फिट किए गए उन मानों के अवशेषों को प्रदर्शित करता है।

यदि फिट किए गए मानों के प्रत्येक स्तर पर अवशेषों का वितरण लगभग बराबर है, तो हम कहते हैं कि निरंतर विचरण धारणा संतुष्ट है।

अन्यथा, यदि अवशेषों का फैलाव व्यवस्थित रूप से बढ़ता या घटता है, तो इस धारणा का उल्लंघन होने की संभावना है।

नोट : इस प्रकार का प्लॉट केवल डेटासेट में रिग्रेशन मॉडल फिट करने के बाद ही बनाया जा सकता है।

निम्नलिखित चार्ट फिट किए गए मानों बनाम अवशेषों के एक प्लॉट का एक उदाहरण दिखाता है जो निरंतर भिन्नता प्रदर्शित करता है:

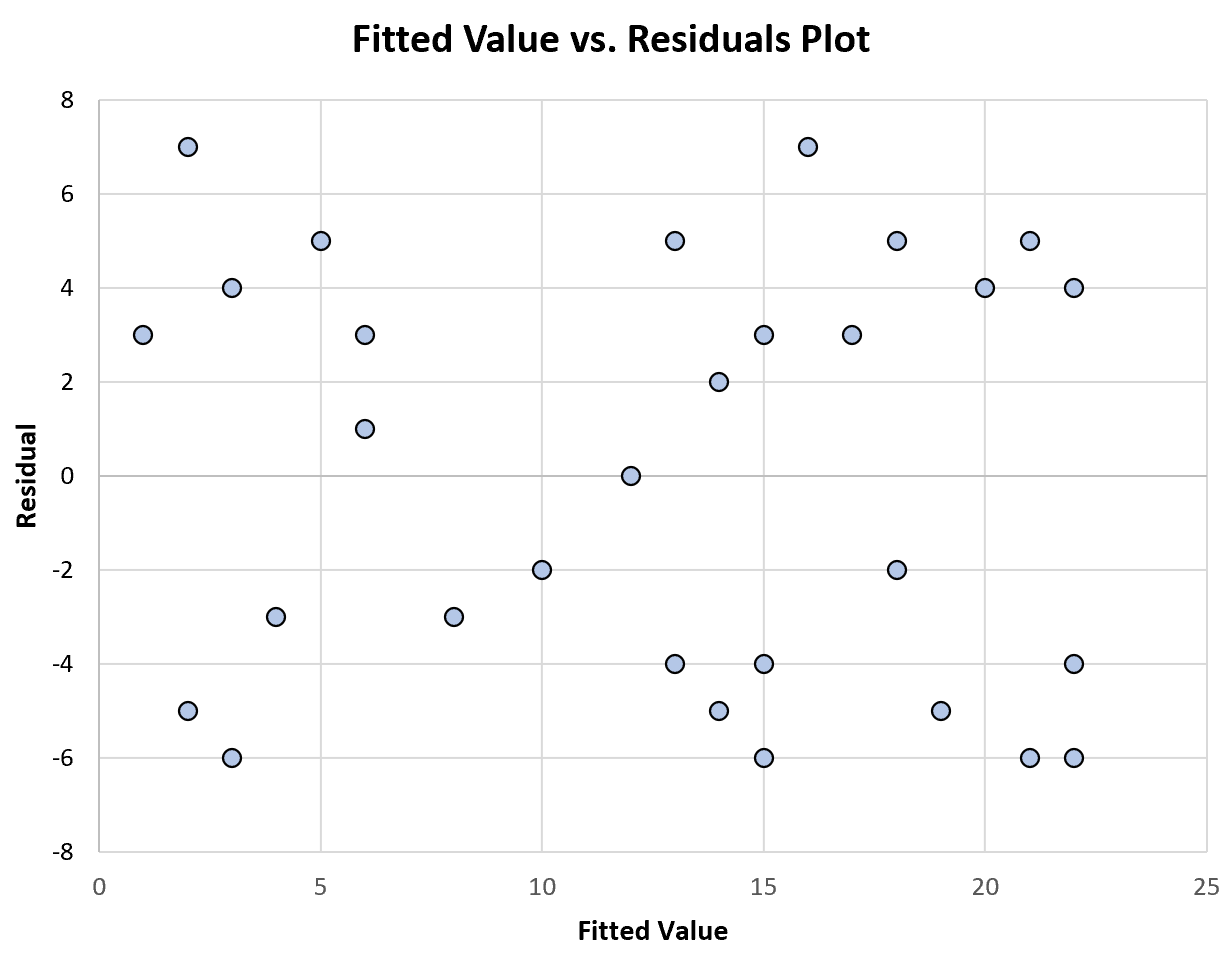
ध्यान दें कि कैसे अवशिष्ट शून्य के चारों ओर बेतरतीब ढंग से बिखरे हुए हैं, बिना किसी विशेष पैटर्न के, फिट किए गए मानों के प्रत्येक स्तर पर लगभग निरंतर भिन्नता के साथ।

निम्नलिखित चार्ट फिट किए गए मानों बनाम अवशेषों के एक प्लॉट का एक उदाहरण दिखाता है जो गैर-स्थिर विचरण प्रदर्शित करता है:

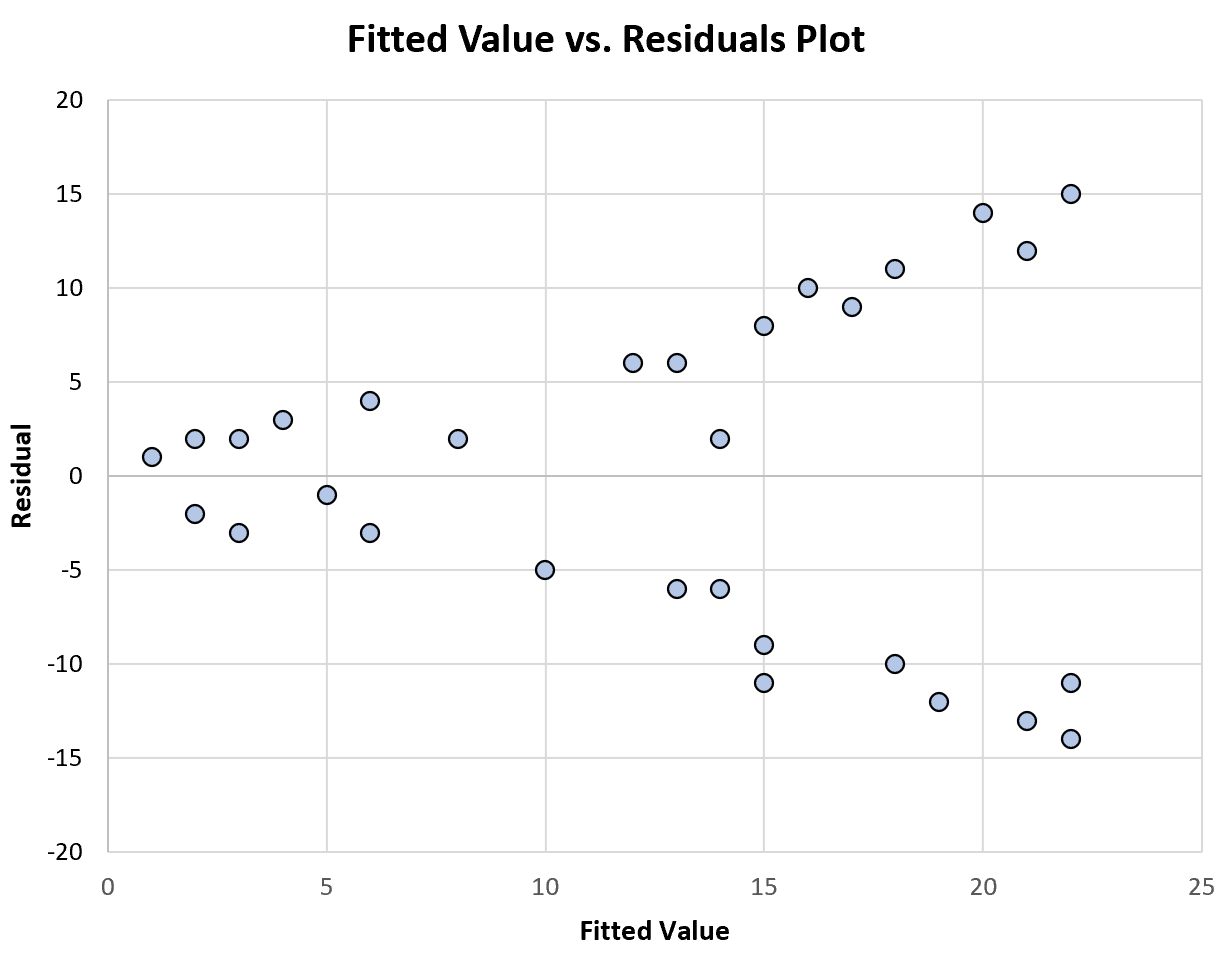
ध्यान दें कि जैसे-जैसे फिट किए गए मान बढ़ते हैं, अवशेषों का वितरण बड़ा होता जाता है। यह गैर-स्थिर विचरण का एक विशिष्ट संकेत है।

यह हमें बताता है कि हमारा प्रतिगमन मॉडल अवशेषों में गैर-निरंतर भिन्नता से ग्रस्त है और इसलिए मॉडल गुणांक अनुमान अविश्वसनीय हैं।

निरंतर विचरण उल्लंघन को कैसे ठीक करें

यदि निरंतर विचरण की धारणा का उल्लंघन किया जाता है, तो इस समस्या को हल करने का सबसे आम तरीका तीन परिवर्तनों में से एक का उपयोग करके प्रतिक्रिया चर को बदलना है:

1. लॉग परिवर्तन: प्रतिक्रिया चर को y से लॉग (y) में बदलें

2. वर्गमूल परिवर्तन: प्रतिक्रिया चर को y से √y में बदलें

3. घनमूल परिवर्तन: प्रतिक्रिया चर को y से y ^1/3 में बदलें

इन परिवर्तनों को करने से, गैर-निरंतर भिन्नता की समस्या आम तौर पर गायब हो जाती है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल रैखिक प्रतिगमन और अवशिष्ट विश्लेषण के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

सरल रेखीय प्रतिगमन का परिचय
एकाधिक रेखीय प्रतिगमन का परिचय
रैखिक प्रतिगमन की चार धारणाएँ
सांख्यिकी में अवशेष क्या हैं?