विद्यार्थी का टी वितरण
यह आलेख बताता है कि स्टूडेंट टी वितरण क्या है और इसका उपयोग किस लिए किया जाता है। इसके अतिरिक्त, छात्र के टी वितरण का ग्राफ दिखाया गया है और इस प्रकार के संभाव्यता वितरण की विशेषताएं क्या हैं।
विद्यार्थी वितरण क्या है?
विद्यार्थी का टी वितरण एक संभाव्यता वितरण है जिसका उपयोग सांख्यिकी में व्यापक रूप से किया जाता है। विशेष रूप से, छात्र के टी वितरण का उपयोग छात्र के टी परीक्षण में दो नमूनों के साधनों के बीच अंतर निर्धारित करने और आत्मविश्वास अंतराल स्थापित करने के लिए किया जाता है।
स्टूडेंट का वितरण 1908 में सांख्यिकीविद् विलियम सीली गॉसेट द्वारा छद्म नाम “स्टूडेंट” के तहत विकसित किया गया था।
छात्र के टी वितरण को उसकी स्वतंत्रता की डिग्री की संख्या से परिभाषित किया जाता है, जो अवलोकनों की कुल संख्या से एक इकाई घटाकर प्राप्त की जाती है। इसलिए, किसी छात्र के t वितरण की स्वतंत्रता की डिग्री निर्धारित करने का सूत्र ν=n-1 है।
![Rendered by QuickLaTeX.com \begin{array}{c}\nu=n-1\\[2ex]X\sim t_\nu\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-1c805dc2d6ca050feb70dad99de53402_l3.png)
विद्यार्थी का t वितरण ग्राफ़
अब जब हम छात्र के वितरण की परिभाषा जानते हैं, तो आइए देखें कि इसका ग्राफ क्या है। तो, नीचे आप ग्राफिक रूप से स्वतंत्रता की विभिन्न डिग्री के साथ छात्र के टी वितरण के कई उदाहरण देख सकते हैं।
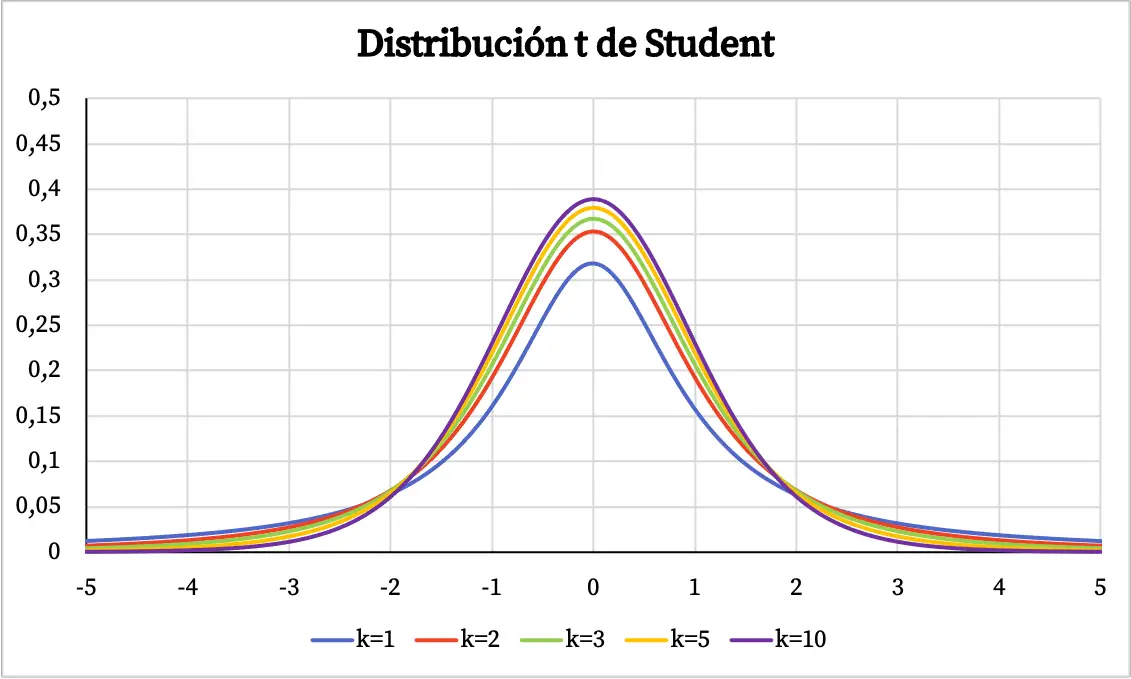
छात्र के टी वितरण के ग्राफ से, निम्नलिखित गुण निकाले जा सकते हैं:
- स्टूडेंट टी वितरण 0 पर केंद्रित सममित है और इसमें घंटी का आकार है।
- विद्यार्थी का t वितरण सामान्य वितरण की तुलना में अधिक फैला हुआ है, अर्थात विद्यार्थी का t वितरण का वक्र व्यापक है।
- विद्यार्थी के वितरण में स्वतंत्रता की जितनी अधिक डिग्री होगी, उसका फैलाव उतना ही कम होगा।
उपरोक्त ग्राफ़ में, छात्र के टी वितरण के घनत्व फ़ंक्शन को उसकी स्वतंत्रता की डिग्री के विरुद्ध प्लॉट किया गया है। हालाँकि, आप नीचे देख सकते हैं कि छात्र के टी वितरण का संचयी संभाव्यता फ़ंक्शन कैसे भिन्न होता है:
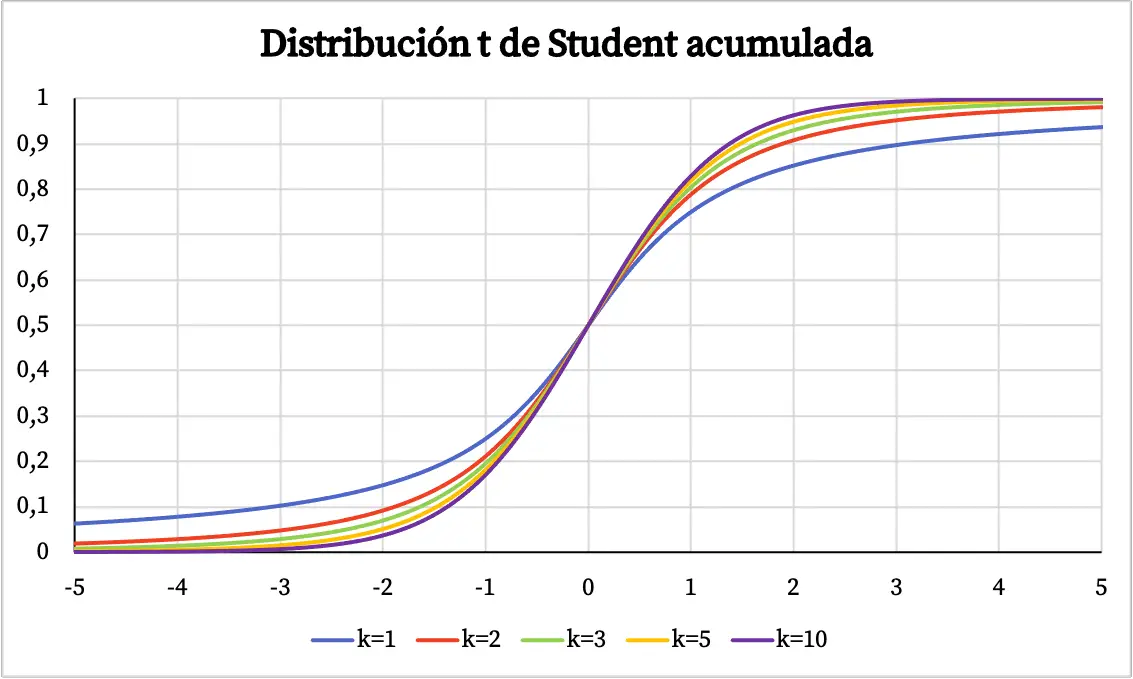
विद्यार्थी के टी वितरण की विशेषताएँ
विद्यार्थी के टी वितरण की सबसे महत्वपूर्ण विशेषताएँ नीचे दिखाई गई हैं।
- स्टूडेंट टी वितरण के डोमेन में वास्तविक संख्याएँ शामिल हैं।
![]()
- एक से अधिक डिग्री की स्वतंत्रता वाले छात्र के टी वितरण के लिए, वितरण का माध्य 0 के बराबर है।
![\begin{array}{c}X\sim t_\nu\\[2ex] E[X]=0 \qquad \text{para }\nu>1\end{array} ” title=”Rendered by QuickLaTeX.com” height=”55″ width=”190″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> किसी छात्र के टी वितरण के विचरण की गणना निम्नलिखित अभिव्यक्ति का उपयोग करके की जा सकती है:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-d4fed5eadcaa1162752aeedb7f8a0906_l3.png)
![\begin{array}{c}X\sim t_\nu\\[2ex] Var(X)=\cfrac{\nu}{\nu-2} \qquad \text{para }\nu>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”245″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> स्वतंत्रता की डिग्री की संख्या की परवाह किए बिना, छात्र के टी वितरण का माध्य और मोड हमेशा 0 होता है।</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-bfdcbc8a5f071a61e091b0ef6f686a16_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{c}Me=0\\[2ex]Mo=0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8d90790fce0c987648c0b30216c82214_l3.png)
- छात्र टी वितरण का घनत्व फ़ंक्शन निम्नलिखित सूत्र द्वारा परिभाषित किया गया है:
![]()
- छात्र के टी वितरण का संचयी संभाव्यता वितरण फ़ंक्शन निम्नलिखित सूत्र द्वारा परिभाषित किया गया है:
![Rendered by QuickLaTeX.com \displaystyle P[X\leq x]=\frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2};-\frac{x^2}{\nu} \right)}{\sqrt{\pi\nu}\,\Gamma \left(\frac{\nu}{2}\right)}](https://statorials.org/wp-content/ql-cache/quicklatex.com-da1e3bdf2d87c3a7dcc89c236958dcec_l3.png)
- 3 से अधिक स्वतंत्रता की डिग्री वाले छात्र के टी वितरण के लिए, असममिति गुणांक शून्य है क्योंकि यह एक सममित वितरण है।
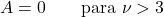
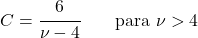 विद्यार्थी के टी वितरण के अनुप्रयोग
विद्यार्थी के टी वितरण के अनुप्रयोग
विद्यार्थी का टी वितरण एक संभाव्यता वितरण है जिसका उपयोग सांख्यिकी में व्यापक रूप से किया जाता है। वास्तव में, यहां तक कि छात्र का टी-टेस्ट भी होता है, जिसका उपयोग परिकल्पनाओं और आत्मविश्वास अंतरालों का परीक्षण करने के लिए किया जाता है।
इस प्रकार, छात्र का टी वितरण हमें दो नमूनों के साधनों के बीच अंतर का विश्लेषण करने की अनुमति देता है, अधिक सटीक रूप से, इसका उपयोग यह निर्धारित करने के लिए किया जाता है कि क्या दो नमूनों में काफी भिन्न साधन हैं। इसी प्रकार, छात्र के टी परीक्षण का उपयोग यह पता लगाने के लिए किया जाता है कि रैखिक प्रतिगमन विश्लेषण से प्राप्त रेखा में ढलान है या नहीं।
संक्षेप में, छात्र के टी वितरण के अनुप्रयोग डेटा सेट के विश्लेषण पर निर्भर करते हैं जो सैद्धांतिक रूप से सामान्य वितरण का पालन करते हैं लेकिन इस प्रकार के वितरण का उपयोग करने के लिए अवलोकनों की कुल संख्या बहुत कम है।