पेरेटो वितरण
यह आलेख बताता है कि आंकड़ों में पेरेटो वितरण क्या है और इसका उपयोग किस लिए किया जाता है। आप पेरेटो वितरण ग्राफ़ और इस प्रकार के संभाव्यता वितरण के गुणों को भी देख पाएंगे।
पेरेटो वितरण क्या है?
पेरेटो वितरण एक सतत संभाव्यता वितरण है जिसका उपयोग पेरेटो सिद्धांत को मॉडल करने के लिए सांख्यिकी में किया जाता है। इसलिए, पेरेटो वितरण एक संभाव्यता वितरण है जिसमें कुछ मान होते हैं जिनके घटित होने की संभावना बाकी मानों की तुलना में बहुत अधिक होती है।
याद रखें कि पेरेटो का नियम, जिसे 80-20 नियम भी कहा जाता है, एक सांख्यिकीय सिद्धांत है जो कहता है कि किसी घटना का अधिकांश कारण जनसंख्या का एक छोटा सा हिस्सा होता है।
पेरेटो वितरण में दो विशिष्ट पैरामीटर हैं: स्केल पैरामीटर x m और आकार पैरामीटर α।
मूल रूप से, पेरेटो वितरण का उपयोग जनसंख्या के भीतर धन के वितरण का वर्णन करने के लिए किया गया था, क्योंकि इसका अधिकांश हिस्सा जनसंख्या के एक छोटे से अनुपात के कारण था। लेकिन वर्तमान में पेरेटो वितरण के कई अनुप्रयोग हैं, उदाहरण के लिए गुणवत्ता नियंत्रण में, अर्थशास्त्र में, विज्ञान में, सामाजिक क्षेत्र में, आदि।
पेरेटो वितरण का नाम अर्थशास्त्री विल्फ्रेडो पेरेटो के नाम पर रखा गया है, जिन्होंने वितरण तैयार किया था। हालाँकि, उन्हें पेरेटो चार्ट के लिए जाना जाता है।
पेरेटो वितरण तालिका
अब जब हम पेरेटो वितरण की परिभाषा जानते हैं, तो आइए ग्राफ़िक रूप से दर्शाए गए पेरेटो वितरण के कई उदाहरण देखें।
तो, नीचे आप देख सकते हैं कि पेरेटो वितरण के घनत्व फ़ंक्शन का ग्राफ़ इसके विशिष्ट मूल्यों के आधार पर कैसा दिखता है:
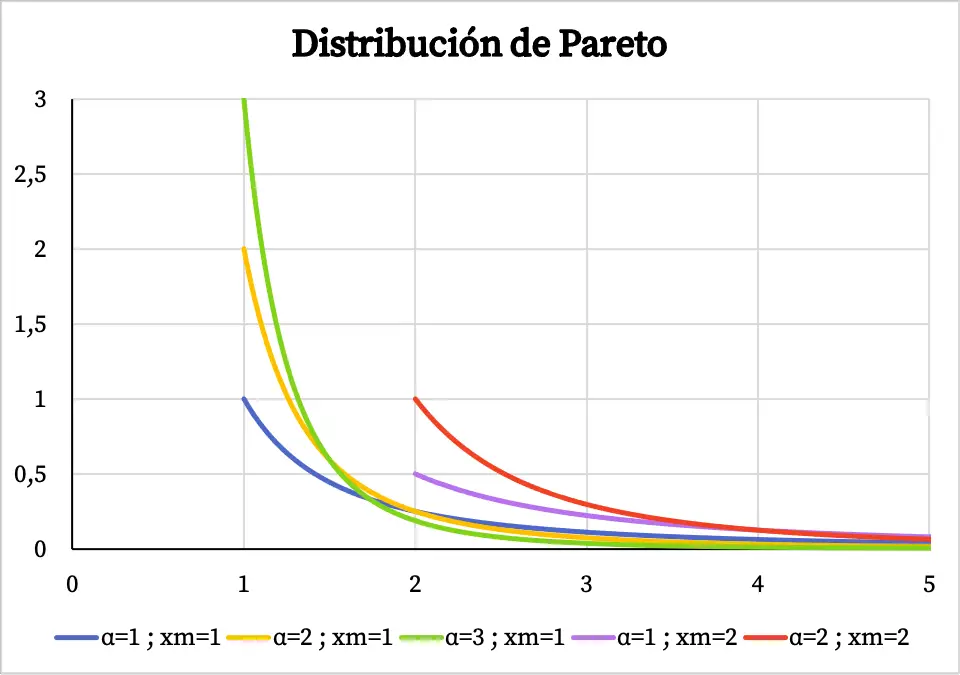
ध्यान दें कि पेरेटो वितरण का डोमेन मान x m से +∞ तक जाता है, यही कारण है कि घनत्व फ़ंक्शन x m के मान से पहले मौजूद नहीं है।
दूसरी ओर, पेरेटो वितरण के संचयी संभाव्यता फ़ंक्शन का ग्राफ इस प्रकार है:
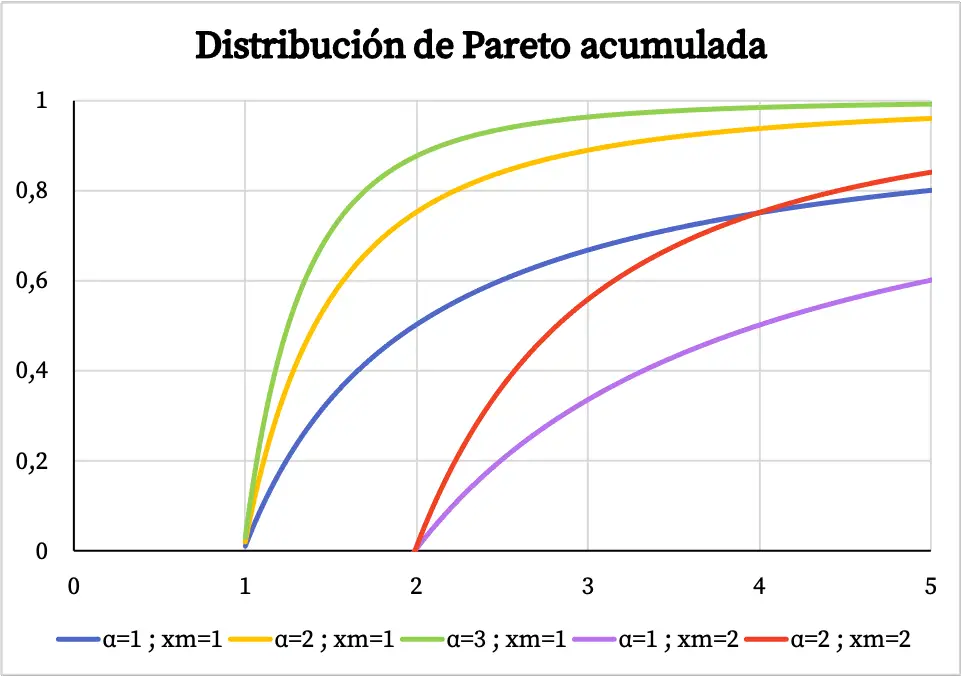
पेरेटो वितरण की विशेषताएँ
संभाव्यता सिद्धांत और सांख्यिकी से संबंधित पेरेटो वितरण की सबसे महत्वपूर्ण विशेषताएं नीचे दी गई हैं।
- पेरेटो वितरण में दो विशिष्ट पैरामीटर हैं जो इसके वक्र को परिभाषित करते हैं: स्केल पैरामीटर x m और आकार पैरामीटर α।
- पेरेटो वितरण के डोमेन में स्केल पैरामीटर से लेकर प्लस इनफिनिटी तक सभी वास्तविक संख्याएँ शामिल हैं।
- यदि α 1 से अधिक है, तो पेरेटो वितरण का माध्य α गुना x m और α घटा 1 के गुणनफल के बराबर है।
![E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”34″ width=”214″ style=”vertical-align: -12px;”></p>
</p>
<ul>
<li> पेरेटो वितरण का विचरण वितरण के दो विशिष्ट मापदंडों पर निर्भर करता है और इसकी गणना निम्नलिखित सूत्र से की जाती है:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6d26513868f9ed6fa45ab0fde0030884_l3.png)
![\displaystyle Me=x_\mathrm{m}\cdot \sqrt[\alpha]{2}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0dc2c772a0a0662ad05f8b22c3cf1ba1_l3.png "Rendered by QuickLaTeX.com")
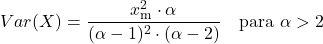
- पेरेटो वितरण का मोड वितरण के स्केल पैरामीटर x m के बराबर है।
- पेरेटो वितरण के घनत्व फलन का सूत्र है:
![\displaystyle P[X=x]=\frac{\alpha\cdot x_m^\alpha}{x^{\alpha+1}}\quad\text{para }x\geq x_m](https://statorials.org/wp-content/ql-cache/quicklatex.com-1e182771cfe3bf9a145a2ee59b9c7eeb_l3.png "Rendered by QuickLaTeX.com")
- इसी प्रकार, पेरेटो वितरण के संचयी संभाव्यता फ़ंक्शन का सूत्र है:
![\displaystyle P[X\leq x]=1-\left(\frac{x_\mathrm{m}}{x}\right)^\alpha](https://statorials.org/wp-content/ql-cache/quicklatex.com-480adc7841b7c72cb4bfecb446ed3fab_l3.png "Rendered by QuickLaTeX.com")
- पेरेटो वितरण का विषमता गुणांक केवल आकार पैरामीटर α पर निर्भर करता है और इसकी अभिव्यक्ति है:
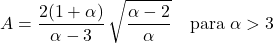
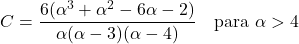
लेखक के बारे में
डॉ. बेंजामिन एंडरसन
नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने