पायथन में द्विचर विश्लेषण कैसे करें: उदाहरणों के साथ

द्विचर विश्लेषण शब्द का तात्पर्य दो चरों के विश्लेषण से है। आप इसे याद रख सकते हैं क्योंकि उपसर्ग “द्वि” का अर्थ “दो” है।

द्विचर विश्लेषण का लक्ष्य दो चरों के बीच संबंध को समझना है

द्विचर विश्लेषण करने के तीन सामान्य तरीके हैं:

1. बिंदु बादल

2. सहसंबंध गुणांक

3. सरल रेखीय प्रतिगमन

निम्नलिखित उदाहरण दिखाता है कि निम्नलिखित पांडा डेटाफ़्रेम का उपयोग करके पायथन में इस प्रकार के प्रत्येक द्विचर विश्लेषण को कैसे निष्पादित किया जाए जिसमें दो चर के बारे में जानकारी शामिल है: (1) अध्ययन में बिताए गए घंटे और (2) 20 अलग-अलग छात्रों द्वारा प्राप्त परीक्षा स्कोर:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                             3, 4, 4, 5, 5, 6, 6, 6, 7, 8],
                   ' score ': [75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                             80, 88, 85, 90, 92, 94, 94, 88, 91, 96]})

#view first five rows of DataFrame
df. head ()

	hours score
0 1 75
1 1 66
2 1 68
3 2 74
4 2 78

1. बिंदु बादल

हम अध्ययन किए गए घंटों बनाम परीक्षा परिणामों का स्कैटरप्लॉट बनाने के लिए निम्नलिखित वाक्यविन्यास का उपयोग कर सकते हैं:

 import matplotlib. pyplot as plt

#create scatterplot of hours vs. score
plt. scatter (df. hours , df. score )
plt. title (' Hours Studied vs. Exam Score ')
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

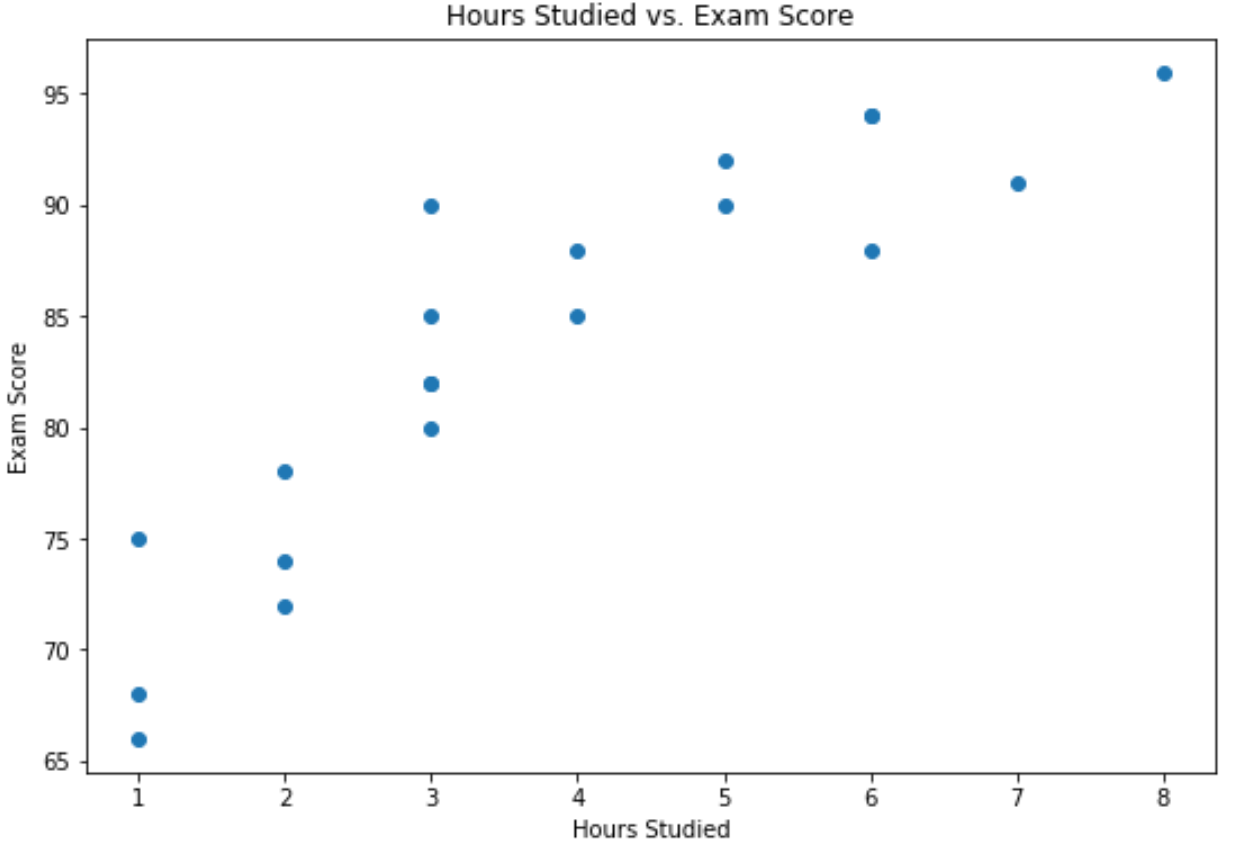
x-अक्ष अध्ययन किए गए घंटों को दर्शाता है और y-अक्ष परीक्षा में अर्जित ग्रेड को दर्शाता है।

ग्राफ़ दिखाता है कि दोनों चरों के बीच एक सकारात्मक संबंध है: जैसे-जैसे अध्ययन के घंटों की संख्या बढ़ती है, परीक्षा के अंक भी बढ़ने लगते हैं।

2. सहसंबंध गुणांक

पियर्सन सहसंबंध गुणांक दो चर के बीच रैखिक संबंध को मापने का एक तरीका है।

सहसंबंध मैट्रिक्स बनाने के लिए हम पांडा में corr() फ़ंक्शन का उपयोग कर सकते हैं:

 #create correlation matrix
df. corr ()

	hours score
hours 1.000000 0.891306
score 0.891306 1.000000

सहसंबंध गुणांक 0.891 निकला। यह अध्ययन किए गए घंटों और परीक्षा ग्रेड के बीच एक मजबूत सकारात्मक सहसंबंध को इंगित करता है।

3. सरल रेखीय प्रतिगमन

सरल रेखीय प्रतिगमन एक सांख्यिकीय पद्धति है जिसका उपयोग हम दो चरों के बीच संबंध को मापने के लिए कर सकते हैं।

हम अध्ययन किए गए घंटों और प्राप्त परीक्षा परिणामों के लिए एक सरल रैखिक प्रतिगमन मॉडल को तुरंत फिट करने के लिए स्टैटमॉडल पैकेज से ओएलएस () फ़ंक्शन का उपयोग कर सकते हैं:

 import statsmodels. api as sm

#define response variable
y = df[' score ']

#define explanatory variable
x = df[[' hours ']]

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.794
Model: OLS Adj. R-squared: 0.783
Method: Least Squares F-statistic: 69.56
Date: Mon, 22 Nov 2021 Prob (F-statistic): 1.35e-07
Time: 16:15:52 Log-Likelihood: -55,886
No. Observations: 20 AIC: 115.8
Df Residuals: 18 BIC: 117.8
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 69.0734 1.965 35.149 0.000 64.945 73.202
hours 3.8471 0.461 8.340 0.000 2.878 4.816
==================================================== ============================
Omnibus: 0.171 Durbin-Watson: 1.404
Prob(Omnibus): 0.918 Jarque-Bera (JB): 0.177
Skew: 0.165 Prob(JB): 0.915
Kurtosis: 2.679 Cond. No. 9.37
==================================================== ============================

फिट किया गया प्रतिगमन समीकरण इस प्रकार है:

परीक्षा स्कोर = 69.0734 + 3.8471*(अध्ययन के घंटे)

यह हमें बताता है कि अध्ययन किया गया प्रत्येक अतिरिक्त घंटा परीक्षा स्कोर में औसतन 3.8471 की वृद्धि से जुड़ा है।

हम अध्ययन किए गए घंटों की कुल संख्या के आधार पर एक छात्र को प्राप्त होने वाले स्कोर की भविष्यवाणी करने के लिए फिट किए गए प्रतिगमन समीकरण का भी उपयोग कर सकते हैं।

उदाहरण के लिए, एक छात्र जो 3 घंटे पढ़ाई करता है उसे 81.6147 का स्कोर मिलना चाहिए:

• परीक्षा स्कोर = 69.0734 + 3.8471*(अध्ययन के घंटे)
• परीक्षा स्कोर = 69.0734 + 3.8471*(3)
• परीक्षा परिणाम = 81.6147

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल द्विचर विश्लेषण के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

द्विचर विश्लेषण का एक परिचय
वास्तविक जीवन में द्विचर डेटा के 5 उदाहरण
सरल रेखीय प्रतिगमन का एक परिचय
पियर्सन सहसंबंध गुणांक का एक परिचय