पॉइसन वितरण या सामान्य वितरण: क्या अंतर है?

पॉइसन वितरण और सामान्य वितरण सांख्यिकी में सबसे अधिक उपयोग किए जाने वाले संभाव्यता वितरणों में से दो हैं।

यह ट्यूटोरियल प्रत्येक वितरण के साथ-साथ वितरण के बीच दो प्रमुख अंतरों का त्वरित विवरण प्रदान करता है।

एक सिंहावलोकन: पॉइसन वितरण

पॉइसन वितरण एक निश्चित समय अंतराल के दौरान k सफलताएँ प्राप्त करने की संभावना का वर्णन करता है।

यदि एक यादृच्छिक चर

पी(एक्स=के) = λ ^के * ई ^{– λ} / के!

सोना:

• λ: एक विशिष्ट अंतराल के दौरान होने वाली सफलताओं की औसत संख्या
• k: सफलताओं की संख्या
• ई: लगभग 2.71828 के बराबर एक स्थिरांक

उदाहरण के लिए, मान लीजिए कि किसी विशेष अस्पताल में प्रति घंटे औसतन 2 जन्म होते हैं। हम एक दिए गए घंटे में 3 जन्मों के अनुभव की संभावना निर्धारित करने के लिए उपरोक्त सूत्र का उपयोग कर सकते हैं:

पी(एक्स=3) = 2 ³ * ई ^-2 /3! = 0.1805

एक निश्चित घंटे में 3 जन्मों का अनुभव होने की संभावना 0.1805 है।

एक सिंहावलोकन: सामान्य वितरण

सामान्य वितरण इस संभावना का वर्णन करता है कि एक यादृच्छिक चर किसी दिए गए अंतराल में एक मान लेता है।

सामान्य वितरण की संभाव्यता घनत्व फ़ंक्शन को इस प्रकार लिखा जा सकता है:

P(X=x) = (1/σ√ 2π )e ^{-1/2((x-μ)/σ) 2}

सोना:

• σ: वितरण का मानक विचलन
• μ: वितरण का माध्य
• x: यादृच्छिक चर का मान

उदाहरण के लिए, मान लीजिए कि ऊदबिलाव की एक निश्चित प्रजाति का वजन आम तौर पर μ = 40 पाउंड और σ = 5 पाउंड के साथ वितरित किया जाता है।

यदि हम इस आबादी से बेतरतीब ढंग से एक ऊदबिलाव का चयन करते हैं, तो हम निम्नलिखित सूत्र का उपयोग करके इसकी संभावना ज्ञात कर सकते हैं कि इसका वजन 38 से 42 पाउंड के बीच है:

पी ( ^{38 < /5) 2} = 0.3108

यादृच्छिक रूप से चुने गए ऊदबिलाव का वजन 38 से 42 पाउंड के बीच होने की संभावना 0.3108 है।

अंतर #1: विवेकशील बनाम. सतत डेटा

पॉइसन वितरण और सामान्य वितरण के बीच पहला अंतर प्रत्येक संभाव्यता वितरण द्वारा मॉडलिंग किए गए डेटा का प्रकार है।

असतत डेटा के साथ काम करते समय एक पॉइसन वितरण का उपयोग किया जाता है जो केवल शून्य के बराबर या उससे अधिक पूर्णांक मान ले सकता है। यहां कुछ उदाहरण दिए गए हैं:

• कॉल सेंटर में प्रति घंटे प्राप्त कॉलों की संख्या
• एक रेस्तरां में प्रतिदिन ग्राहकों की संख्या
• प्रति माह कार दुर्घटनाओं की संख्या

प्रत्येक परिदृश्य में, यादृच्छिक चर केवल 0, 1, 2, 3, आदि मान ले सकता है।

निरंतर डेटा के साथ काम करते समय एक सामान्य वितरण का उपयोग किया जाता है जो नकारात्मक अनंत से सकारात्मक अनंत तक कोई भी मान ले सकता है। यहां कुछ उदाहरण दिए गए हैं:

• एक निश्चित जानवर का वजन
• एक निश्चित पौधे की ऊंचाई
• महिलाओं की मैराथन बार
• तापमान सेल्सियस में

इन परिदृश्यों में, यादृच्छिक चर कोई भी मान ले सकते हैं जैसे -11.3, 21.343435, 85, आदि।

अंतर #2: वितरण का आकार

पॉइसन वितरण और सामान्य वितरण के बीच दूसरा अंतर वितरण के आकार में है।

एक सामान्य वितरण में हमेशा एक घंटी का आकार होगा:

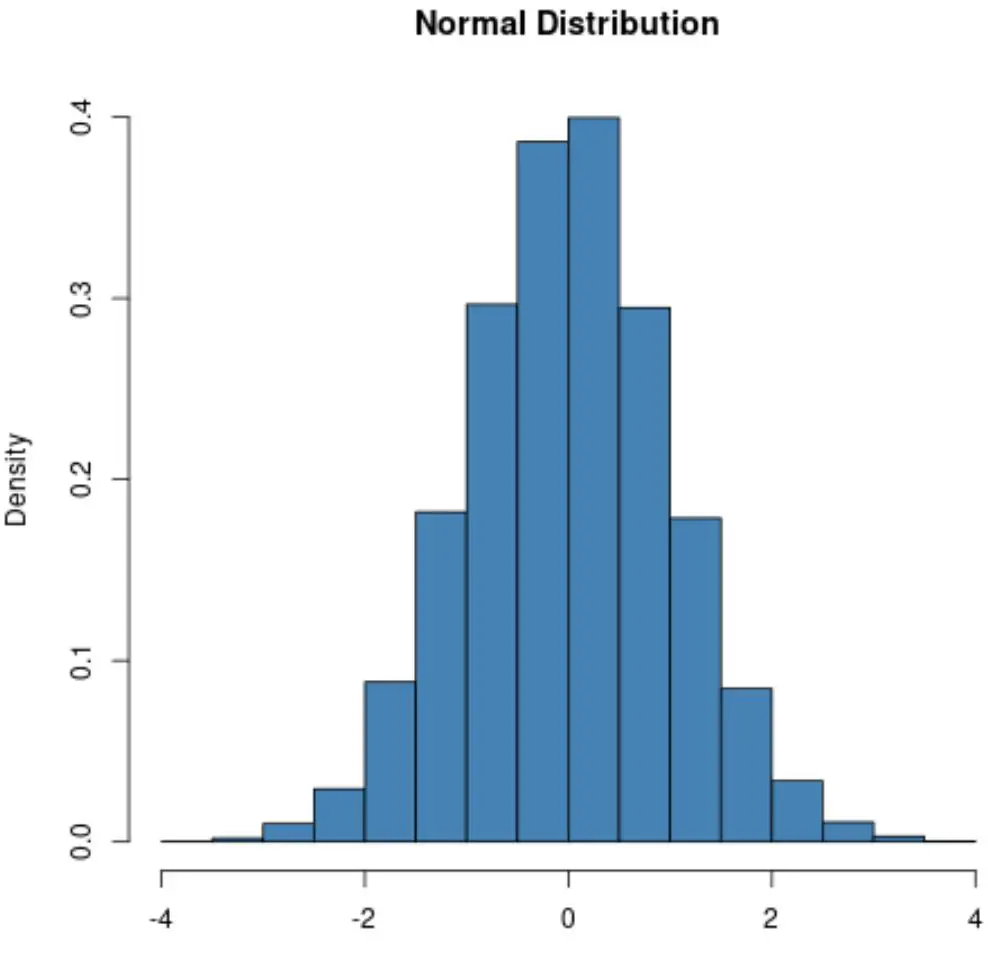
हालाँकि, पॉइसन वितरण का आकार वितरण के औसत मूल्य के आधार पर भिन्न होता है।

उदाहरण के लिए, μ = 3 जैसे माध्य के लिए एक छोटे मान वाला पॉइसन वितरण दृढ़ता से दाएं-तिरछा होगा:

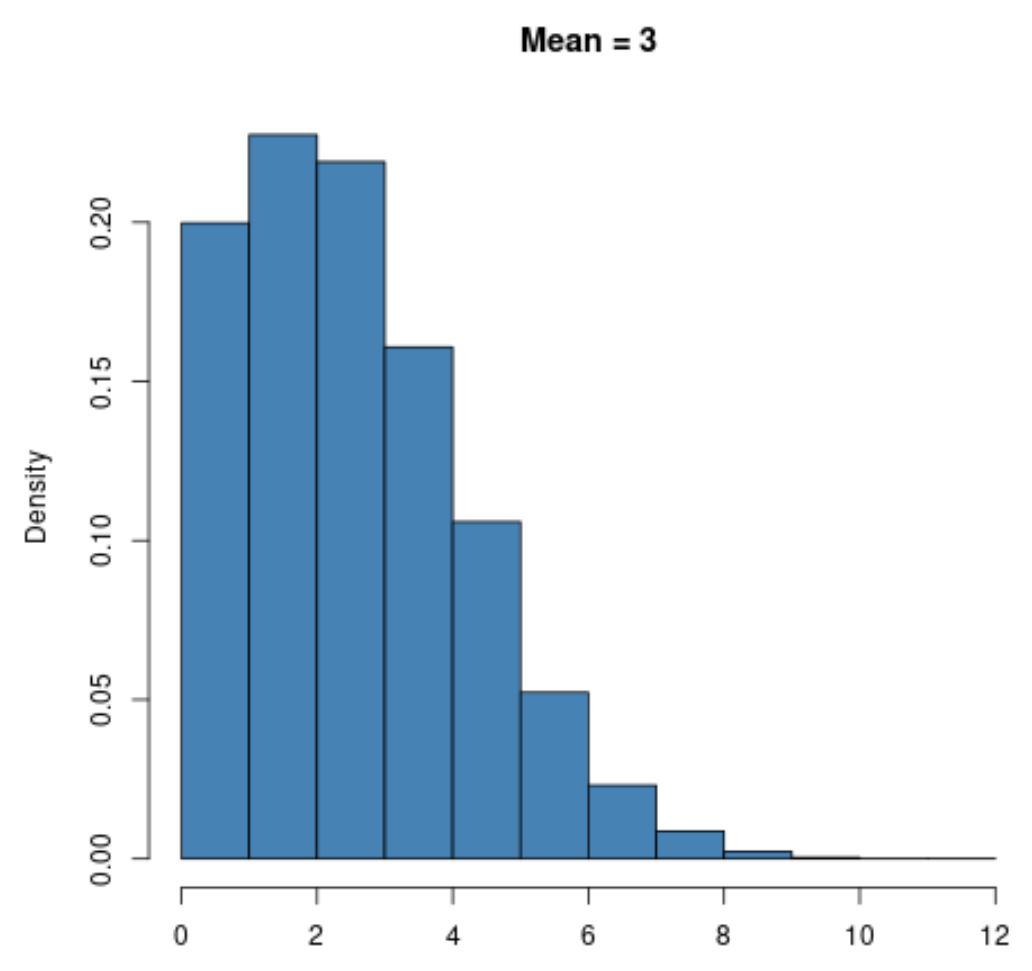
हालाँकि, μ = 20 जैसे बड़े माध्य मान वाला एक पॉइसन वितरण सामान्य वितरण की तरह ही एक घंटी का आकार प्रदर्शित करेगा:

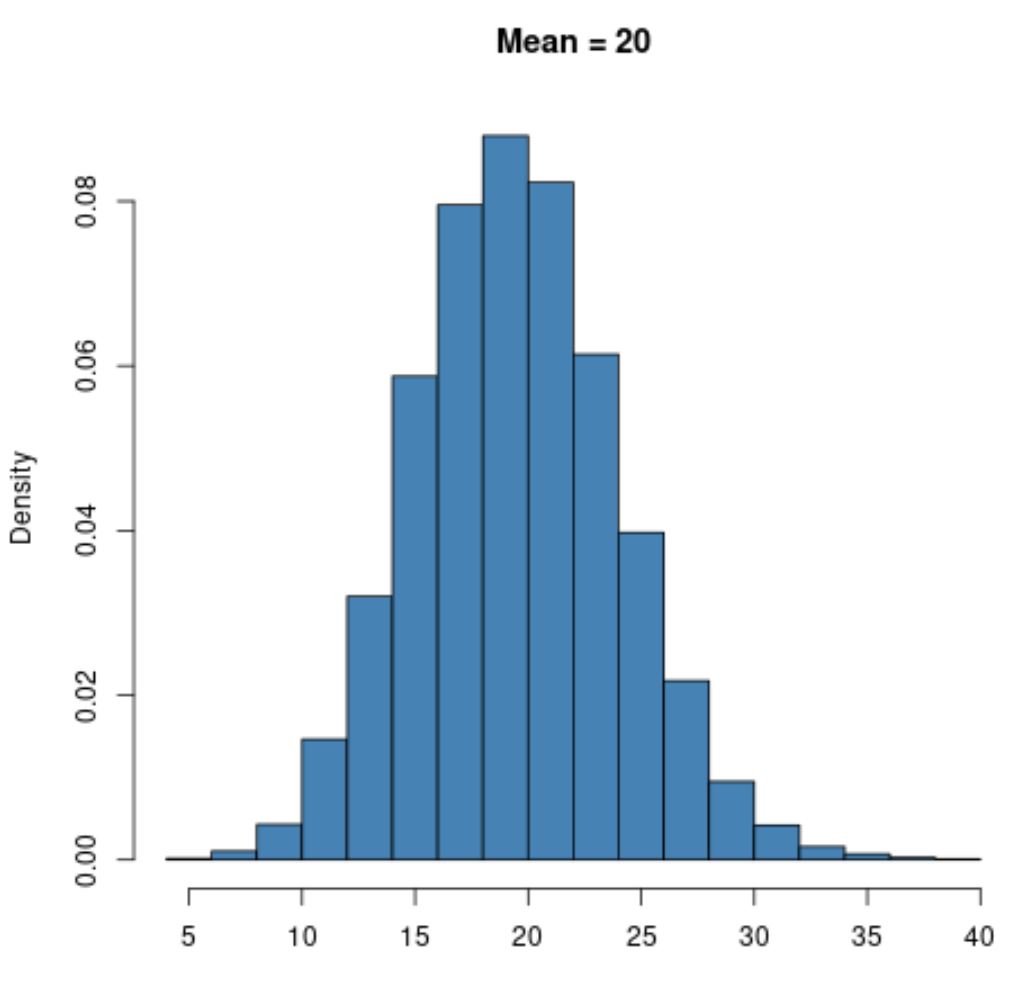
ध्यान दें कि पॉइसन वितरण की निचली सीमा हमेशा शून्य होगी, माध्य के मूल्य की परवाह किए बिना, क्योंकि पॉइसन वितरण का उपयोग केवल शून्य के बराबर या उससे अधिक पूर्णांक मानों के साथ किया जा सकता है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल पॉइसन वितरण के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

पॉइसन वितरण का परिचय
पॉइसन वितरण की चार परिकल्पनाएँ
पॉइसन वितरण के 5 ठोस उदाहरण

निम्नलिखित ट्यूटोरियल सामान्य वितरण के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

सामान्य वितरण का परिचय
सामान्य वितरण के 6 ठोस उदाहरण
सामान्य वितरण डेटासेट जेनरेटर